18 25 In Percentage
renascent
Sep 23, 2025 · 5 min read
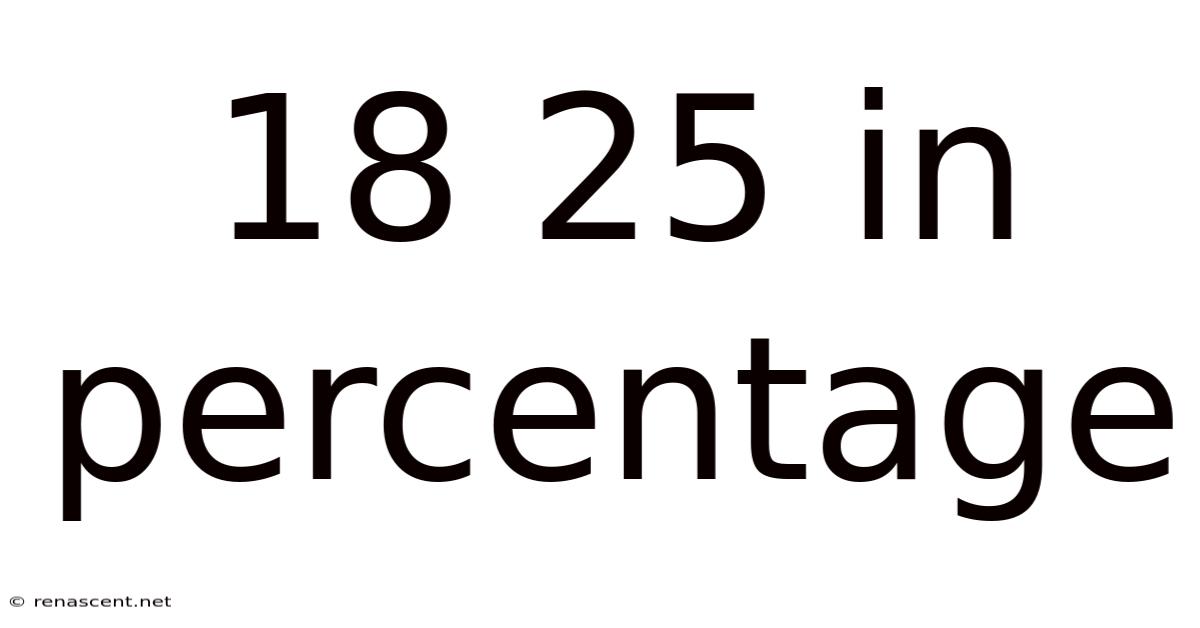
Table of Contents
Decoding 18/25 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance to science. This article delves into the process of converting the fraction 18/25 into a percentage, providing a step-by-step explanation, exploring different methods, and addressing common misconceptions. We'll also explore the broader context of percentage calculations and their practical uses.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. The number on top is called the numerator, representing the portion considered, while the number on the bottom is the denominator, representing the total number of parts. A percentage, denoted by the symbol %, represents a fraction out of 100. Therefore, converting a fraction to a percentage means expressing the fraction as a number out of 100.
Method 1: Converting the Fraction to a Decimal then to a Percentage
This is arguably the most straightforward method. It involves two steps:
-
Convert the fraction to a decimal: To do this, divide the numerator (18) by the denominator (25).
18 ÷ 25 = 0.72
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%).
0.72 × 100 = 72%
Therefore, 18/25 is equal to 72%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the definition of percentage as a fraction out of 100. We aim to find an equivalent fraction to 18/25 where the denominator is 100.
To achieve this, we need to determine what number we can multiply the denominator (25) by to get 100. This is simple: 100 ÷ 25 = 4.
Crucially, whatever we do to the denominator, we must do to the numerator to maintain the equivalence of the fraction. Therefore, we multiply both the numerator and denominator by 4:
(18 × 4) / (25 × 4) = 72/100
Since a percentage is a fraction out of 100, 72/100 directly translates to 72%.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between fractions and percentages. We can set up a proportion:
18/25 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
18 × 100 = 25 × x
1800 = 25x
x = 1800 ÷ 25
x = 72
Therefore, 18/25 is equal to 72%.
Practical Applications of Percentage Calculations
Understanding percentage calculations isn't just an academic exercise; it's a crucial life skill with numerous real-world applications:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, a 72% discount on a $100 item would mean a saving of $72.
-
Science: Percentage is frequently used to express experimental results, concentrations (e.g., 72% alcohol solution), and statistical data. A survey might report that 72% of respondents prefer a particular product.
-
Everyday Life: Calculating tips in restaurants, understanding sale prices, and interpreting statistics in news reports all involve percentages. For example, knowing that 72% of your monthly budget is allocated to essential expenses allows for better financial planning.
Common Mistakes to Avoid
While the conversion of 18/25 to a percentage is relatively straightforward, several common mistakes can occur:
-
Incorrect order of operations: When converting fractions to decimals, always divide the numerator by the denominator. Reversing this order leads to an incorrect result.
-
Forgetting to multiply by 100: A common oversight is neglecting to multiply the resulting decimal by 100 to express it as a percentage.
-
Misunderstanding the concept of percentage: A clear understanding of what a percentage represents – a fraction out of 100 – is essential for accurate calculations.
Expanding on the Concept: Beyond 18/25
The methods outlined above are applicable to converting any fraction to a percentage. For example, let's consider the fraction 3/4:
- Decimal Method: 3 ÷ 4 = 0.75; 0.75 × 100 = 75%
- Equivalent Fraction Method: (3 × 25) / (4 × 25) = 75/100 = 75%
- Proportion Method: 3/4 = x/100; 300 = 4x; x = 75%
Frequently Asked Questions (FAQs)
Q1: Can I convert a percentage back into a fraction?
Yes, absolutely. To convert a percentage to a fraction, simply place the percentage value over 100 and simplify the fraction. For example, 75% becomes 75/100, which simplifies to 3/4.
Q2: What if the decimal resulting from the fraction division is long and non-terminating?
For non-terminating decimals, round the decimal to the desired level of accuracy before multiplying by 100 to express it as a percentage. The level of accuracy required will depend on the context of the problem.
Q3: Are there any online tools or calculators to help with this conversion?
Yes, many websites and apps offer fraction-to-percentage calculators. These tools can be helpful for verifying your calculations or for handling more complex fractions.
Conclusion
Converting 18/25 to a percentage – resulting in 72% – is a fundamental mathematical skill with widespread applications. By mastering the different methods presented in this article, including the decimal, equivalent fraction, and proportion methods, you'll develop a solid foundation for understanding and applying percentage calculations in various aspects of your life. Remember to practice these methods to build proficiency and avoid common pitfalls. This understanding will empower you to confidently tackle percentage-based problems in academic settings, professional contexts, and everyday scenarios.
Latest Posts
Latest Posts
-
Lanseria International Airport Lanseria
Sep 23, 2025
-
22 Kgs In Pounds
Sep 23, 2025
-
75 Cm In Inches
Sep 23, 2025
-
29 Centimeters To Inches
Sep 23, 2025
-
Average Speed Of Swimmer
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 18 25 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.