19 Divided By 4
renascent
Sep 21, 2025 · 6 min read
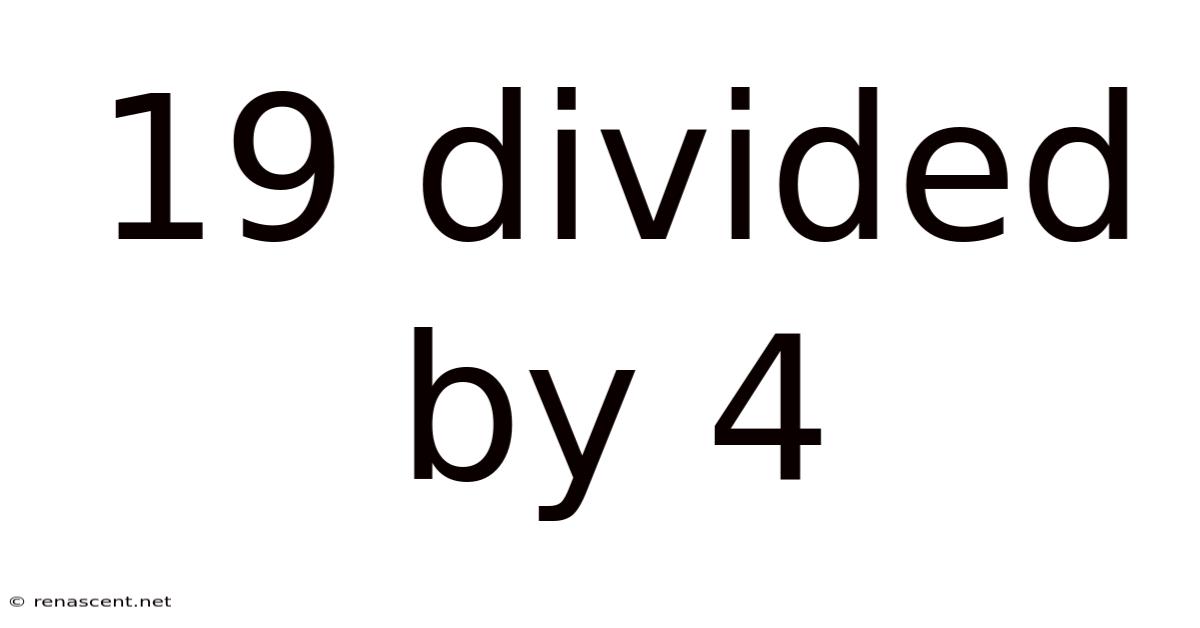
Table of Contents
Diving Deep into 19 Divided by 4: Exploring Division, Remainders, and Real-World Applications
The seemingly simple question, "What is 19 divided by 4?", opens a door to a surprisingly rich exploration of mathematical concepts. This article will not only provide the answer but delve into the underlying principles of division, the significance of remainders, and illustrate how this basic operation applies to various real-world scenarios. We'll unravel the complexities hidden within this straightforward calculation, making it accessible to everyone from elementary school students to those looking for a refresher on fundamental arithmetic.
Understanding Division: More Than Just Sharing
Division, at its core, is the process of splitting a quantity into equal groups. When we say "19 divided by 4," we're essentially asking: "If we have 19 items, how many groups of 4 can we make?" This seemingly simple question underlies many complex mathematical operations and forms the basis for various problem-solving strategies.
The standard notation for division is 19 ÷ 4 or 19/4. Both notations represent the same mathematical operation. We can also think of division as the inverse operation of multiplication. If 4 multiplied by some number equals 19, that number is the result of 19 divided by 4. However, as we'll see, there’s a crucial difference between whole numbers and the introduction of decimals or fractions.
Calculating 19 Divided by 4: The Process
Let's break down the calculation step-by-step:
-
Find the Quotient: We start by finding out how many times 4 goes into 19 without exceeding 19. We can do this through repeated subtraction or by using long division. 4 goes into 19 four times (4 x 4 = 16). This '4' is our quotient.
-
Determine the Remainder: After subtracting 16 from 19, we have 3 left over. This '3' is our remainder. It represents the portion of 19 that cannot be evenly divided into groups of 4.
Therefore, 19 divided by 4 is 4 with a remainder of 3. We can express this as:
- 19 ÷ 4 = 4 R 3 (where 'R' stands for remainder)
Representing the Result: Decimals and Fractions
The result can also be expressed as a decimal or a fraction, providing different perspectives on the division:
-
Decimal Representation: To get the decimal representation, we continue the division process. We add a decimal point to 19 and append zeros. We then continue dividing until we reach a desired level of accuracy or a repeating pattern emerges. This gives us 4.75.
-
Fractional Representation: The remainder (3) becomes the numerator, and the divisor (4) becomes the denominator, resulting in the fraction 3/4. Therefore, 19/4 can also be expressed as 4 and 3/4 (a mixed number).
The choice between decimal and fractional representations often depends on the context of the problem. Decimals are generally preferred for measurements and calculations where precision is important. Fractions are useful when dealing with proportions and ratios, as they often provide a clearer understanding of the relationship between the parts and the whole.
The Significance of the Remainder
The remainder is a critical element in division. It reveals that the division isn't exact; there's a portion that's 'left over.' In some contexts, the remainder is simply discarded (rounding down), while in others, it holds significant meaning.
For instance:
-
Sharing Candy: If you have 19 candies and want to divide them equally among 4 friends, each friend gets 4 candies, and you have 3 candies left over.
-
Cutting Fabric: If you have 19 meters of fabric and need to cut 4-meter pieces, you can cut 4 pieces, leaving 3 meters remaining.
-
Programming: In computer science, remainders are often used in modular arithmetic, forming the basis of various algorithms and cryptographic techniques. The remainder operation (modulo operation, denoted by %) provides information about divisibility. For example, 19 % 4 = 3 indicates that 19 leaves a remainder of 3 when divided by 4.
Real-World Applications: Beyond Simple Division
The concept of division with remainders permeates various aspects of daily life:
-
Scheduling and Time Management: Dividing tasks into equal segments, allocating time for activities, and planning projects often involve dealing with remainders, representing tasks that spill over into the next time slot.
-
Inventory Management: Determining the number of items needed to fill orders or restock shelves frequently requires understanding remainders to ensure sufficient quantities.
-
Engineering and Construction: Calculations in construction, manufacturing, and engineering frequently involve dividing resources and materials, and remainders play a crucial role in optimizing material usage and preventing waste.
-
Finance: Dividing financial resources, calculating interest, and distributing payments might result in remainders, reflecting fractional amounts.
-
Data Analysis: Statistical analyses, especially those involving frequency distributions or data grouping, use division and remainders to categorize and interpret data effectively.
Deeper Dive: Long Division and its Importance
While we touched upon the process, let's examine long division more thoroughly. It is a systematic method for performing division, particularly useful for larger numbers. Here's how long division works for 19 ÷ 4:
4 R 3
4 | 19
16
3
-
Divide: 4 goes into 19 four times (4).
-
Multiply: Multiply the quotient (4) by the divisor (4): 4 x 4 = 16.
-
Subtract: Subtract the product (16) from the dividend (19): 19 - 16 = 3.
-
Remainder: The result (3) is the remainder.
Long division provides a structured approach to handle more complex division problems, breaking them down into manageable steps. Mastering long division is essential for understanding more advanced mathematical concepts, including fractions, decimals, and algebraic operations.
Frequently Asked Questions (FAQs)
Q1: What is the simplest way to explain 19 divided by 4 to a child?
A1: Imagine you have 19 cookies, and you want to share them equally among 4 friends. Each friend gets 4 cookies (that's the quotient), and you have 3 cookies left over (that's the remainder).
Q2: Why can't we just say 19 divided by 4 is 4.75 and ignore the remainder?
A2: While 4.75 is the exact decimal equivalent, the remainder is crucial for certain applications. For example, if you're dividing physical objects, you can't have 0.75 of a cookie or a piece of fabric. The remainder represents the leftover portion that needs to be accounted for.
Q3: What are some common mistakes people make when dividing with remainders?
A3: Common errors include:
-
Forgetting the remainder: Ignoring the remainder and only providing the quotient.
-
Incorrectly calculating the remainder: Making mistakes during the subtraction step in long division.
-
Misunderstanding the concept of the quotient: Confusing the quotient with the dividend or the divisor.
Q4: How does understanding 19 divided by 4 help in solving more complex problems?
A4: Understanding division with remainders provides a foundational understanding of:
-
Fractions: The remainder forms the numerator of the fractional part of the result.
-
Decimals: The remainder leads to the decimal portion of the result.
-
Modulo arithmetic: A crucial tool in computer science and other fields.
-
Proportions and ratios: Understanding how parts relate to the whole.
Conclusion: The Power of a Simple Calculation
The seemingly simple calculation of 19 divided by 4 unveils a wealth of mathematical concepts and real-world applications. From understanding the basic principles of division and the importance of remainders to applying these concepts in diverse scenarios, this exploration highlights the power and versatility of even the most fundamental mathematical operations. By grasping the nuances of division, we equip ourselves with a vital tool for navigating various challenges in academics, daily life, and professional pursuits. The ability to understand, interpret, and apply these principles is a key element of numerical literacy and a foundational skill for further mathematical learning.
Latest Posts
Latest Posts
-
Forrest Gump Table Tennis
Sep 21, 2025
-
56 C To F
Sep 21, 2025
-
Convert Rad Sec To Rpm
Sep 21, 2025
-
7 X 5 2
Sep 21, 2025
-
What Are Bobby Calves
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 19 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.