7 X 5 2
renascent
Sep 21, 2025 · 5 min read
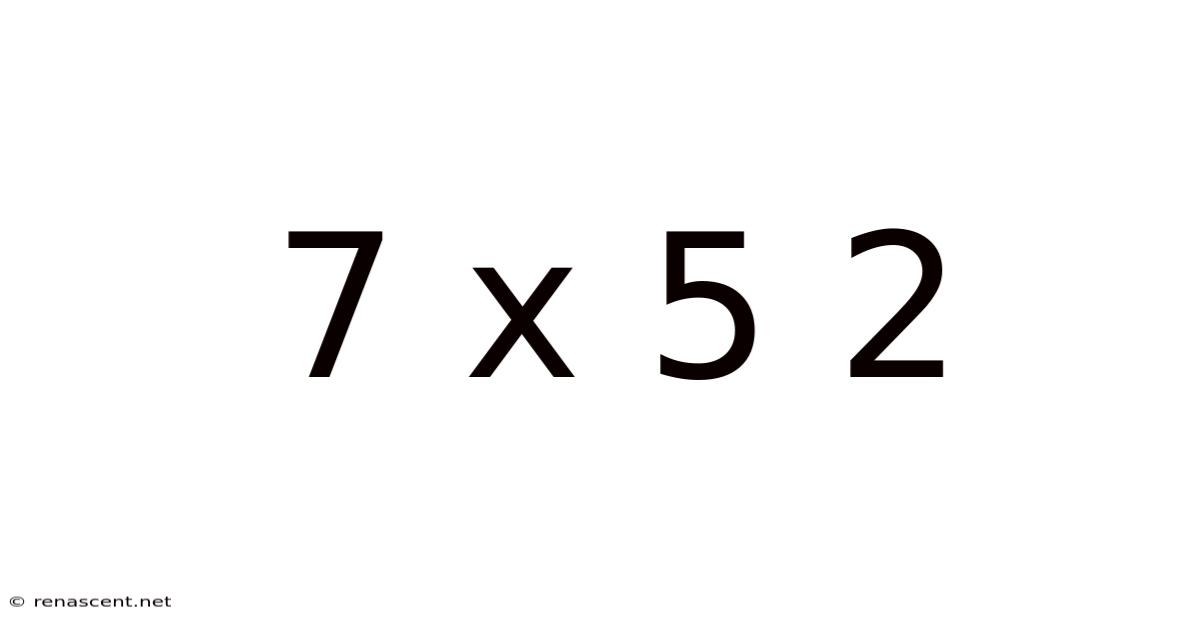
Table of Contents
Decoding the Enigma: A Deep Dive into 7 x 5 = 2 (and Why It's Not True)
This article explores the seemingly simple mathematical equation, 7 x 5 = 2, examining why this statement is incorrect, delving into the fundamental principles of multiplication, and exploring potential misunderstandings that might lead to such a conclusion. We'll unravel the mystery behind this false equation, offering a comprehensive understanding suitable for all learning levels, from elementary school students to adults seeking to refresh their mathematical foundations. Understanding multiplication is crucial for a solid grasp of arithmetic and serves as a building block for more complex mathematical concepts.
Introduction: The Foundation of Multiplication
Multiplication, at its core, represents repeated addition. When we say 7 x 5, we are essentially asking: "What is the sum of seven fives?" Or, equivalently, "What is the result of adding five to itself seven times?" This fundamental understanding is key to comprehending why 7 x 5 cannot equal 2. Let's break down the process:
5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
Therefore, the correct answer to 7 x 5 is 35, not 2. The discrepancy between the commonly known answer and the erroneous claim highlights the importance of accuracy in mathematical calculations and the need to understand the underlying principles.
Exploring Potential Sources of Error: Why Someone Might Think 7 x 5 = 2
While the correct answer is undeniably 35, it's important to explore the potential reasons why someone might arrive at the incorrect answer of 2. Understanding these potential errors is crucial for effective teaching and learning. Several possibilities exist:
-
Misunderstanding of Multiplication: A fundamental misunderstanding of the concept of multiplication as repeated addition could lead to incorrect calculations. Someone might mistakenly interpret the equation as a simple addition or subtraction problem.
-
Errors in Calculation: Simple arithmetic errors during the calculation process can lead to incorrect results. This is particularly prevalent when working with larger numbers or more complex calculations, where overlooking a single step can lead to a significant error. Even experienced mathematicians can make these mistakes.
-
Cognitive Bias: Cognitive biases, such as confirmation bias (seeking evidence to confirm existing beliefs) or anchoring bias (over-relying on initial information), could influence the interpretation of the equation. Someone might wrongly assume the answer to be 2 without proper calculation and then justify this incorrect assumption.
-
Typographical Errors: A simple typographical error could easily lead to the misinterpretation of the equation. A misplaced digit or incorrect symbol could lead to a completely incorrect outcome.
-
Misremembering Multiplication Facts: It's possible someone misremembered the multiplication fact of 7 x 5. While rote memorization isn't the only path to understanding, knowing basic multiplication facts is incredibly efficient.
A Step-by-Step Approach to Solving 7 x 5
To reinforce the correct method, let's break down the multiplication of 7 x 5 using several approaches:
1. Repeated Addition:
As discussed earlier, the most fundamental way to solve 7 x 5 is through repeated addition:
5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
2. Using a Multiplication Table:
A multiplication table is a valuable tool for quickly recalling multiplication facts. Locating the intersection of row 7 and column 5 reveals the correct answer: 35.
3. Visual Representation:
Imagine seven rows, each containing five objects (apples, marbles, etc.). Counting all the objects would demonstrate a total of 35. This visual approach is especially helpful for younger learners.
4. Array Method:
Another visual approach is creating an array. Draw a rectangle with seven rows and five columns. By counting the squares within the rectangle, we again arrive at 35.
The Importance of Accuracy in Mathematics: Beyond 7 x 5
The seemingly simple equation 7 x 5 = 2 underscores the importance of accuracy in all aspects of mathematics. Inaccurate calculations can have significant consequences, ranging from minor inconveniences to major errors with severe implications.
Consider these examples:
-
Everyday Calculations: Incorrect calculations in everyday tasks like budgeting, shopping, or calculating tips can result in financial losses.
-
Engineering and Construction: Inaccurate calculations in engineering and construction projects can lead to structural failures, safety hazards, and costly rework.
-
Scientific Research: Errors in scientific calculations can invalidate research findings, leading to wasted resources and potentially harmful conclusions.
-
Programming and Software Development: Mistakes in programming can result in software malfunctions, security vulnerabilities, and data loss.
The focus on accuracy is not merely about getting the "right answer"; it's about developing a solid understanding of the underlying principles and developing problem-solving skills that translate to diverse fields.
Frequently Asked Questions (FAQ)
-
Q: Why is multiplication important?
-
A: Multiplication is a fundamental arithmetic operation that simplifies repeated addition, providing an efficient method for solving many real-world problems. It forms the basis for more advanced mathematical concepts like algebra, calculus, and statistics.
-
Q: How can I improve my multiplication skills?
-
A: Practice is key. Use multiplication tables, visual aids, and interactive online resources to strengthen your understanding and memorization of multiplication facts. Regular practice and focusing on the conceptual understanding (repeated addition) will significantly aid skill improvement.
-
Q: What are some common mistakes in multiplication?
-
A: Common mistakes include misunderstanding the concept of multiplication, arithmetic errors, misremembering facts, and overlooking carrying digits (in multi-digit multiplication).
-
Q: Is there a way to check my multiplication answers?
-
A: Yes! You can use reverse operations (division) to check your answer. For instance, if 7 x 5 = 35, then 35 ÷ 7 = 5 and 35 ÷ 5 = 7. This method helps verify the accuracy of your calculations.
Conclusion: The Power of Understanding
The seemingly trivial equation 7 x 5 = 2 serves as a powerful reminder of the importance of accuracy and a strong foundation in basic mathematics. While it's easy to dismiss a simple multiplication error, the underlying principle is far-reaching. Understanding the building blocks of arithmetic—addition, subtraction, multiplication, and division—is crucial for success in more advanced mathematical disciplines and for navigating the quantitative aspects of everyday life. By understanding the concepts behind multiplication and practicing regularly, we can avoid errors and build confidence in our mathematical abilities. The journey to mathematical proficiency is not about memorizing facts in isolation but about grasping the underlying principles and applying them with accuracy and precision. The ability to critically evaluate mathematical statements, such as the incorrect claim 7 x 5 = 2, demonstrates a deeper understanding of the subject and fosters a more analytical approach to problem-solving.
Latest Posts
Latest Posts
-
The Monsters Are Due
Sep 21, 2025
-
145 F In C
Sep 21, 2025
-
4000 Minutes To Hours
Sep 21, 2025
-
Strong Grip Blox Fruits
Sep 21, 2025
-
5 12 3 4
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 7 X 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.