195 Divided By 15
renascent
Sep 25, 2025 · 6 min read
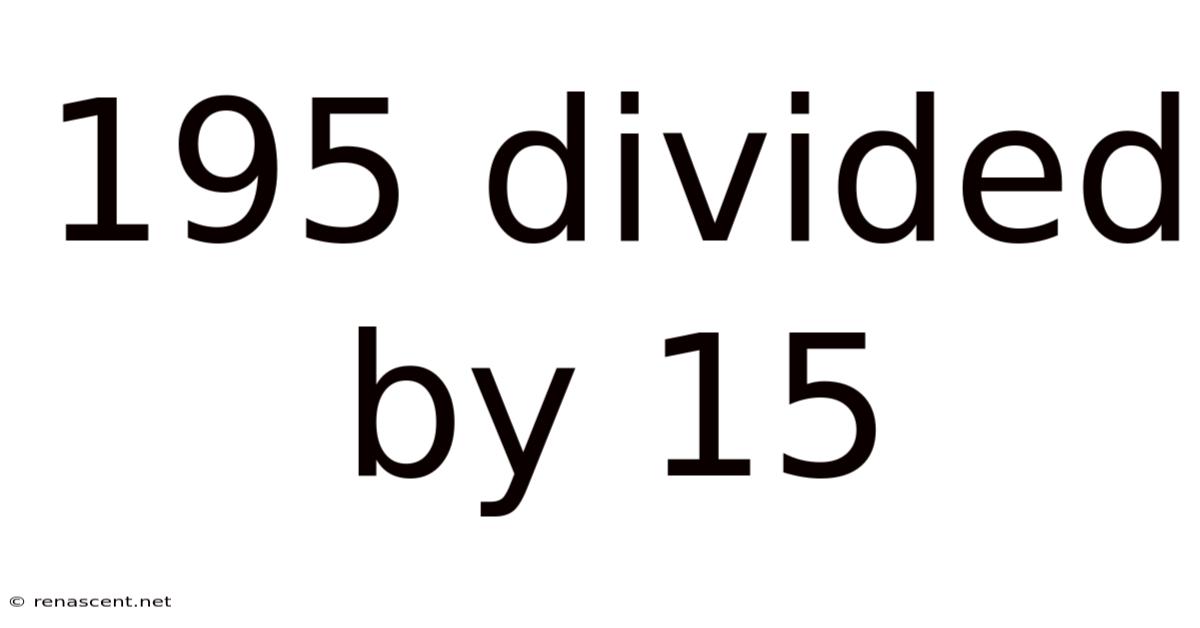
Table of Contents
Unveiling the Simplicity: A Deep Dive into 195 Divided by 15
Dividing 195 by 15 might seem like a simple arithmetic problem, something easily solved with a calculator. But beneath the surface of this seemingly straightforward calculation lies a wealth of mathematical concepts and techniques that can deepen our understanding of numbers and operations. This article will explore the division of 195 by 15, going beyond the simple answer to explore various methods of solving it, its applications in real-world scenarios, and the underlying mathematical principles involved. This exploration will cover different approaches, including long division, mental math techniques, and the conceptual understanding of factors and multiples. By the end, you'll not only know the answer but also understand why it's the answer and how this seemingly simple problem connects to broader mathematical ideas.
Understanding the Problem: 195 ÷ 15
The problem, 195 ÷ 15, asks us to find how many times the number 15 goes into 195. This is a fundamental concept in division: partitioning a larger number into equal groups of a smaller number. The result of this operation is called the quotient, while any remaining amount after the equal partitioning is called the remainder (though, as we'll see, there's no remainder in this particular case). Understanding this basic framework is essential before we delve into the different solution methods.
Method 1: Long Division – A Step-by-Step Approach
Long division is a systematic method for performing division, particularly useful when dealing with larger numbers. Let's break down the process of dividing 195 by 15 using long division:
-
Set up the problem: Write the dividend (195) inside the long division symbol and the divisor (15) outside.
15 | 195 -
Divide the first digit(s): Ask yourself, "How many times does 15 go into 19?" The answer is 1. Write the 1 above the 9 in the dividend.
1 15 | 195 -
Multiply and subtract: Multiply the quotient (1) by the divisor (15), which equals 15. Write 15 below the 19 and subtract: 19 - 15 = 4.
1 15 | 195 -15 4 -
Bring down the next digit: Bring down the next digit from the dividend (5), placing it next to the 4, making it 45.
1 15 | 195 -15 45 -
Divide again: Ask yourself, "How many times does 15 go into 45?" The answer is 3. Write the 3 above the 5 in the dividend.
13 15 | 195 -15 45 -
Multiply and subtract: Multiply the quotient (3) by the divisor (15), which equals 45. Write 45 below the 45 and subtract: 45 - 45 = 0.
13 15 | 195 -15 45 -45 0 -
The quotient is 13: Since there is no remainder, the answer to 195 divided by 15 is 13.
Method 2: Mental Math Techniques – Leveraging Number Sense
While long division provides a systematic approach, mental math techniques can be quicker for simpler problems. For 195 ÷ 15, we can employ several strategies:
-
Factoring: We can break down both the dividend and the divisor into their prime factors. 195 can be factored as 3 x 5 x 13, and 15 as 3 x 5. Notice that 3 x 5 is a common factor to both numbers. Dividing both by 3 x 5 (which equals 15), we are left with 13. Therefore, 195 ÷ 15 = 13.
-
Approximation and Adjustment: We can approximate 15 to 10 or 20 for a quick estimation. 195 divided by 10 is 19.5, and 195 divided by 20 is 9.75. Since 15 is between 10 and 20, the answer should be between these two values. Refining this estimate using number sense quickly leads to the answer 13.
Method 3: Repeated Subtraction – A Conceptual Approach
Repeated subtraction is a more visual and conceptual approach to division, especially helpful for younger learners. It involves repeatedly subtracting the divisor from the dividend until the result is zero or less than the divisor.
- Start with 195.
- Subtract 15: 195 - 15 = 180. (1 time)
- Subtract 15 again: 180 - 15 = 165. (2 times)
- Continue this process until you reach zero.
By counting how many times you subtract 15, you arrive at the quotient, which is 13. While this method is less efficient for large numbers, it effectively illustrates the core concept of division as repeated subtraction.
Real-World Applications: Putting Division into Practice
The division of 195 by 15 is not just an abstract mathematical exercise; it has numerous real-world applications. For instance:
-
Distributing items: Imagine you have 195 apples to distribute equally among 15 baskets. The division would tell you that each basket would receive 13 apples.
-
Calculating unit price: If a pack of 15 pencils costs 195 cents, dividing 195 by 15 gives you the price of a single pencil (13 cents).
-
Determining average: If 15 students scored a total of 195 points on a test, the average score per student would be 13 points.
These examples showcase the practical utility of division in everyday situations, highlighting its importance beyond the realm of abstract mathematics.
Exploring Further: Factors, Multiples, and Divisibility Rules
The problem 195 ÷ 15 allows us to explore the concepts of factors, multiples, and divisibility rules.
-
Factors: A factor is a number that divides another number without leaving a remainder. Both 3 and 5 are factors of 15, and they are also factors of 195. This is why we were able to use the factoring method in our mental math approach.
-
Multiples: A multiple is a number that is the product of a given number and another integer. 195 is a multiple of 15 (15 x 13 = 195).
-
Divisibility Rules: Understanding divisibility rules can help in quickly determining if a number is divisible by another. Since 195 is divisible by both 3 and 5 (the sum of its digits is divisible by 3, and it ends in 5), it's also divisible by 15 (because 15 = 3 x 5). This knowledge speeds up the calculation process and strengthens our number sense.
Frequently Asked Questions (FAQs)
Q: What is the remainder when 195 is divided by 15?
A: There is no remainder when 195 is divided by 15. The division is exact.
Q: Are there other ways to solve 195 ÷ 15?
A: Yes, various other methods exist, including using a calculator or employing different algorithms for long division.
Q: Why is understanding division important?
A: Division is fundamental to numerous mathematical concepts and real-world applications, including calculating averages, proportions, ratios, and rates.
Conclusion: Beyond the Answer – Embracing the Process
While the answer to 195 ÷ 15 is simply 13, the journey to arrive at this answer is far more enriching. This exploration has highlighted various methods of solving the problem, from the methodical approach of long division to the intuitive strategies of mental math. We've also touched upon the practical applications of division and the broader mathematical concepts intertwined with this seemingly simple calculation. The key takeaway is not just knowing the answer but appreciating the underlying principles and the multiple pathways to reach it. This understanding fosters a deeper appreciation for mathematics and enhances problem-solving skills applicable across various disciplines. The seemingly simple act of dividing 195 by 15 unveils a world of mathematical richness and practicality.
Latest Posts
Latest Posts
-
5 Divided By 2 5
Sep 25, 2025
-
17 50 As A Percentage
Sep 25, 2025
-
0 625 In Fraction Form
Sep 25, 2025
-
Why Does Frogs Croak
Sep 25, 2025
-
Brazil Major Tourist Attractions
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 195 Divided By 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.