2 5 4 15
renascent
Sep 20, 2025 · 6 min read
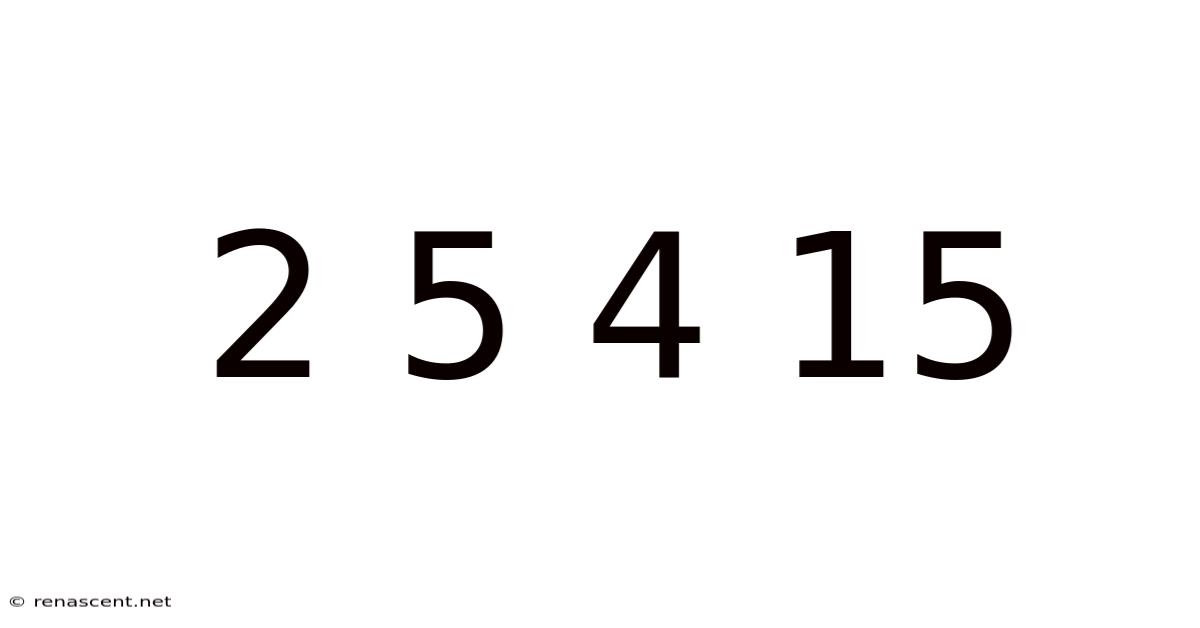
Table of Contents
Unlocking the Mystery of 2 5 4 15: A Deep Dive into Number Sequences and Pattern Recognition
The seemingly simple sequence 2, 5, 4, 15 presents a fascinating challenge for those interested in mathematics and pattern recognition. At first glance, it appears random. However, a closer examination reveals a hidden logic, multiple potential solutions, and a valuable lesson in the power of observation and creative problem-solving. This article will explore several interpretations of this sequence, delve into the underlying mathematical concepts, and offer a framework for approaching similar numerical puzzles. Understanding sequences like this enhances critical thinking skills and provides a stepping stone to more complex mathematical concepts.
The Initial Approach: Identifying Potential Patterns
When faced with a number sequence, the first step is to look for obvious patterns. Let's analyze the sequence 2, 5, 4, 15:
- Differences: Calculating the differences between consecutive numbers yields 3, -1, 11. This doesn't immediately reveal a clear pattern.
- Ratios: Examining the ratios between consecutive numbers (5/2, 4/5, 15/4) also doesn't show a consistent relationship.
- Squares and Cubes: Checking if the numbers are squares or cubes of integers doesn't produce any obvious connections.
The absence of easily discernible patterns suggests that a more nuanced approach is necessary. We need to consider more complex relationships between the numbers.
Method 1: Alternating Patterns
One possible interpretation involves recognizing two separate, interleaved patterns. Let's divide the sequence into two subsequences:
- Subsequence 1: 2, 4... This subsequence appears to be based on multiplication by 2. The next number would logically be 8.
- Subsequence 2: 5, 15... This subsequence appears to be based on multiplication by 3. The next number would logically be 45.
Following this alternating pattern, the sequence could continue as 2, 5, 4, 15, 8, 45, 16, 135, and so on. This solution highlights the importance of considering multiple perspectives when analyzing numerical sequences. It demonstrates that seemingly random numbers can often be explained by underlying, intertwined patterns.
Method 2: Operations Between Consecutive Numbers
Another approach involves analyzing the operations performed between consecutive numbers. Let's examine the relationships:
- 2 to 5: Adding 3 (2 + 3 = 5)
- 5 to 4: Subtracting 1 (5 - 1 = 4)
- 4 to 15: Adding 11 (4 + 11 = 15)
The differences between these operations (3, -1, 11) don't initially reveal a pattern. However, let's explore a different perspective. Consider a pattern that combines addition and multiplication:
- 2 to 5: (2 * 2) + 1 = 5
- 5 to 4: (5/5) = 1 (This step doesn't clearly fit the pattern and needs further investigation)
- 4 to 15: (4 * 3) + 3 = 15
Here, we see a pattern emerge of multiplying by a number then adding an amount. However, the operation between 5 and 4 breaks the pattern, suggesting this method might be incomplete or require a refinement of the rules.
Method 3: Introducing a Hidden Function
Perhaps the sequence is governed by a more complex mathematical function. This approach moves beyond simple arithmetic operations and introduces the possibility of a function that maps one number in the sequence to the next. We could postulate a function, f(x), where:
- f(2) = 5
- f(5) = 4
- f(4) = 15
Finding a single function that satisfies all three conditions might prove challenging. However, we could explore piecewise functions or functions with parameters that could be adjusted to fit the data.
Method 4: Considering Context and External Factors
Sometimes, the solution to a number sequence puzzle lies outside the purely mathematical realm. The sequence might be part of a larger problem with additional context that helps unveil the hidden pattern. For example:
- Real-world data: The numbers might represent measurements, quantities, or events in a specific scenario.
- Coding or encryption: The sequence could be a code or part of an encryption algorithm.
- A game or puzzle: It might be a component of a larger game or puzzle with additional clues.
Without additional context, this approach is difficult to apply definitively to the sequence 2, 5, 4, 15.
The Importance of Exploring Multiple Solutions
The 2, 5, 4, 15 sequence illustrates the fact that there often isn’t one single “right” answer when dealing with number sequences. Different mathematical approaches can lead to plausible explanations. The key is to explore multiple perspectives and to be open to the possibility of complex or unconventional patterns. This process itself is valuable for enhancing critical thinking and problem-solving abilities.
Expanding the Scope: Related Concepts and Further Exploration
Understanding number sequences like 2, 5, 4, 15 is a stepping stone to more advanced mathematical concepts:
- Fibonacci Sequence: A classic example of a recursive sequence where each number is the sum of the two preceding ones (1, 1, 2, 3, 5, 8...).
- Arithmetic and Geometric Progressions: Sequences where the difference (arithmetic) or ratio (geometric) between consecutive terms remains constant.
- Recurrence Relations: Mathematical equations that define the terms of a sequence based on previous terms.
- Generating Functions: Powerful tools for analyzing and manipulating sequences.
Exploring these concepts will deepen your understanding of pattern recognition and provide a more robust toolkit for approaching similar mathematical puzzles.
Frequently Asked Questions (FAQ)
Q: Is there a single definitive answer to the sequence 2, 5, 4, 15?
A: No. As shown above, several interpretations and solutions are possible, depending on the assumptions made and the methods employed. The absence of additional context allows for multiple plausible explanations.
Q: How can I improve my skills in solving number sequence puzzles?
A: Practice is crucial. Start with simpler sequences and gradually increase the complexity. Develop a systematic approach involving differences, ratios, squares, cubes, and exploring potential patterns. Be open to unconventional solutions.
Q: What mathematical concepts are most relevant to solving these types of problems?
A: A strong understanding of basic arithmetic operations, algebra, and an intuitive grasp of pattern recognition are essential. Knowledge of more advanced topics like recurrence relations and generating functions can prove helpful for more complex sequences.
Q: Are there any online resources available to learn more about number sequences?
A: Yes, numerous online resources, including educational websites, mathematical forums, and online courses, provide information and practice problems related to number sequences and pattern recognition.
Conclusion: The Value of Creative Problem-Solving
The seemingly simple sequence 2, 5, 4, 15 serves as a powerful illustration of the importance of creative problem-solving and exploring multiple perspectives. While there may not be a single definitive answer, the process of investigating various solutions enhances critical thinking skills and provides a gateway to deeper understanding of mathematical concepts. The challenge lies not only in finding a solution but also in the development of a systematic and adaptable approach to tackling such problems. The journey of exploring this sequence underscores the rewarding nature of mathematical inquiry and the beauty of uncovering hidden patterns within seemingly random data. By embracing this approach, you’ll not only improve your mathematical abilities but also foster a more flexible and creative mindset applicable to various aspects of life.
Latest Posts
Latest Posts
-
68 5 Inches In Ft
Sep 20, 2025
-
64 Divided By 2
Sep 20, 2025
-
196 Kg To Lbs
Sep 20, 2025
-
40 Km To Knots
Sep 20, 2025
-
10 Of A Million
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 2 5 4 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.