64 Divided By 2
renascent
Sep 20, 2025 · 6 min read
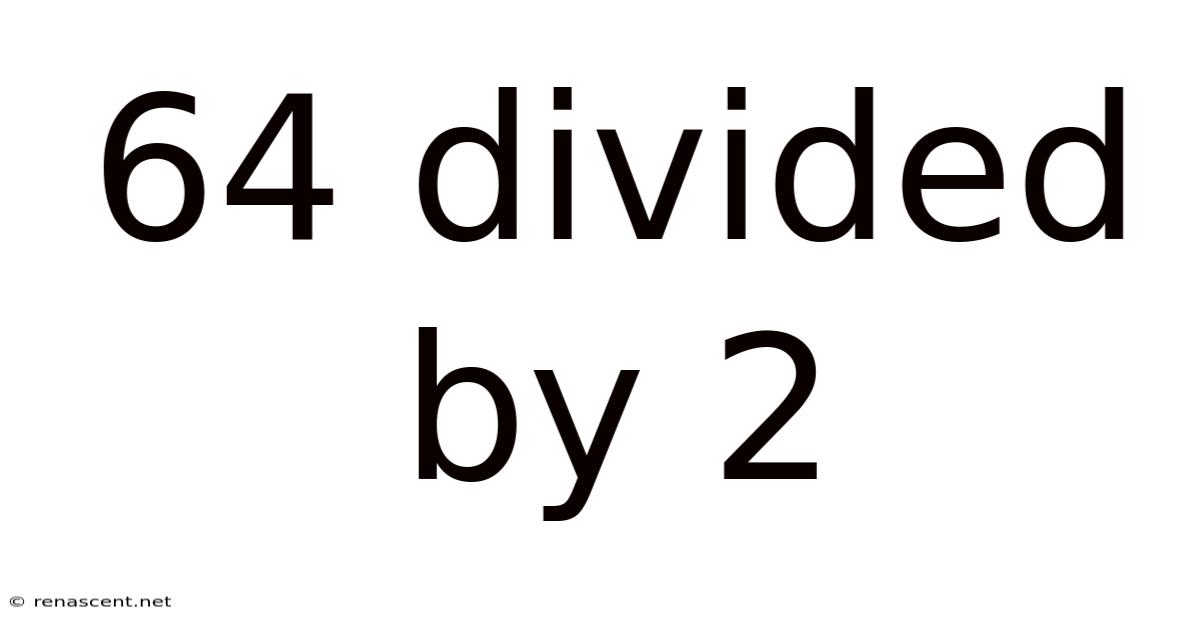
Table of Contents
64 Divided by 2: A Deep Dive into Simple Division and its Applications
This article explores the seemingly simple arithmetic problem of 64 divided by 2, delving far beyond the basic answer. We'll examine the process of division, its underlying principles, different methods for solving it, real-world applications, and even connect it to more advanced mathematical concepts. Understanding this seemingly basic operation is crucial for building a solid foundation in mathematics and problem-solving skills. This comprehensive guide is designed for learners of all levels, from elementary school students to those looking to refresh their fundamental arithmetic skills.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. In the context of 64 divided by 2 (often written as 64 ÷ 2 or 64/2), we're asking: "How many times does 2 fit into 64?" The answer, as we'll demonstrate extensively, is 32. But understanding why this is the answer is just as important as knowing the answer itself.
Method 1: Long Division
Long division is a formal method used to divide larger numbers. While 64 divided by 2 might seem too simple for this method, it serves as an excellent introduction to the process.
-
Set up the problem: Write 64 inside a division symbol (like a long parenthesis), with 2 outside.
2 | 64 -
Divide the tens: How many times does 2 go into 6? It goes in 3 times (3 x 2 = 6). Write 3 above the 6.
3 2 | 64 -
Multiply and subtract: Multiply the quotient (3) by the divisor (2): 3 x 2 = 6. Subtract this from the dividend (6): 6 - 6 = 0.
3 2 | 64 -6 -- 0 -
Bring down the ones: Bring down the next digit (4).
3 2 | 64 -6 -- 04 -
Divide the ones: How many times does 2 go into 4? It goes in 2 times (2 x 2 = 4). Write 2 above the 4.
32 2 | 64 -6 -- 04 -
Multiply and subtract: Multiply the quotient (2) by the divisor (2): 2 x 2 = 4. Subtract this from the remaining dividend (4): 4 - 4 = 0.
32 2 | 64 -6 -- 04 -4 -- 0
Therefore, 64 divided by 2 equals 32.
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the divisor (2) from the dividend (64) until you reach 0. The number of times you subtract represents the quotient.
64 - 2 = 62 62 - 2 = 60 60 - 2 = 58 ...and so on.
While effective for smaller numbers, this method becomes tedious for larger divisions. However, it visually reinforces the concept of division as repeated subtraction.
Method 3: Halving
Since we are dividing by 2, we can simply halve the number 64. This is a quick and intuitive method for dividing by 2. Half of 64 is 32.
Method 4: Using Multiplication (Inverse Operation)
Division and multiplication are inverse operations. This means that if you multiply the quotient by the divisor, you get the dividend. To find the answer to 64 ÷ 2, we can ask: "What number multiplied by 2 equals 64?" The answer, of course, is 32. This method is particularly useful for checking your answer after using another division method.
Real-World Applications
The simple division of 64 by 2 has numerous real-world applications:
- Sharing Equally: If you have 64 candies and want to share them equally between 2 friends, each friend gets 32 candies.
- Measurement Conversions: Converting units often involves division. For example, if you know a distance is 64 inches and you need to convert it to feet (1 foot = 12 inches), you would divide 64 by 12. While not directly 64/2, it demonstrates the practical application of division.
- Calculating Averages: Finding the average of two numbers sometimes requires division. For instance, if you scored 64 and 64 on two tests, the average score is (64+64)/2 = 64. Again, not directly 64/2 but illustrates the context.
- Ratio and Proportion: Dividing 64 by 2 can be part of solving ratio and proportion problems. For example, if a recipe calls for 64 grams of flour for 2 servings, you would divide 64 by 2 to find out how many grams of flour are needed per serving.
- Data Analysis: Division is fundamental in statistical analysis for tasks like calculating rates, frequencies, and proportions.
Connecting to Advanced Concepts
While seemingly basic, 64 divided by 2 forms a foundation for more complex mathematical concepts:
- Binary Numbers: The binary number system, the foundation of modern computing, uses only two digits (0 and 1). Understanding division by 2 is crucial for converting decimal numbers (like 64) into binary.
- Fractions and Decimals: 64/2 can be represented as a fraction (64/2 = 32/1 = 32) or a decimal (32.0). This highlights the connection between different number representations.
- Algebra: Division is a key operation in solving algebraic equations. For example, the equation 2x = 64 can be solved by dividing both sides by 2, resulting in x = 32.
- Calculus: Division plays a role in various calculus concepts, including derivatives and integrals, although in much more complex scenarios.
Frequently Asked Questions (FAQ)
- What is the remainder when 64 is divided by 2? There is no remainder because 64 is evenly divisible by 2.
- Can I use a calculator to solve 64 divided by 2? Absolutely! Calculators are useful tools for performing quick calculations.
- Why is division important? Division is essential for solving a wide range of problems across various fields, from everyday tasks to advanced scientific calculations. It helps us understand relationships between quantities and solve problems involving sharing, scaling, and proportions.
- Are there other ways to calculate 64 divided by 2? Yes, you could use mental math techniques, such as recognizing that 64 is an even number and easily divisible by 2. You could also break it down: 60/2 + 4/2 = 30 + 2 = 32.
Conclusion: The Significance of Simplicity
The seemingly simple calculation of 64 divided by 2 provides a gateway to understanding fundamental mathematical principles and their wide-ranging applications. Mastering this basic operation is not just about getting the right answer (32), but about developing a deeper understanding of the process itself, its underlying logic, and its relevance to more complex mathematical concepts and real-world problem-solving. By exploring different methods and understanding the underlying principles, you build a strong foundation for future mathematical endeavors. The simplicity of this calculation belies its importance in nurturing mathematical thinking and problem-solving skills. It's a stepping stone to more advanced mathematics, and a reminder that even the most fundamental concepts hold profound significance.
Latest Posts
Latest Posts
-
9000 Seconds To Minutes
Sep 20, 2025
-
600 Divided By 4
Sep 20, 2025
-
405 Minutes To Hours
Sep 20, 2025
-
136 Pounds To Kilos
Sep 20, 2025
-
Oth Nathan And Lucas
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 64 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.