2/8 As A Decimal
renascent
Sep 16, 2025 · 5 min read
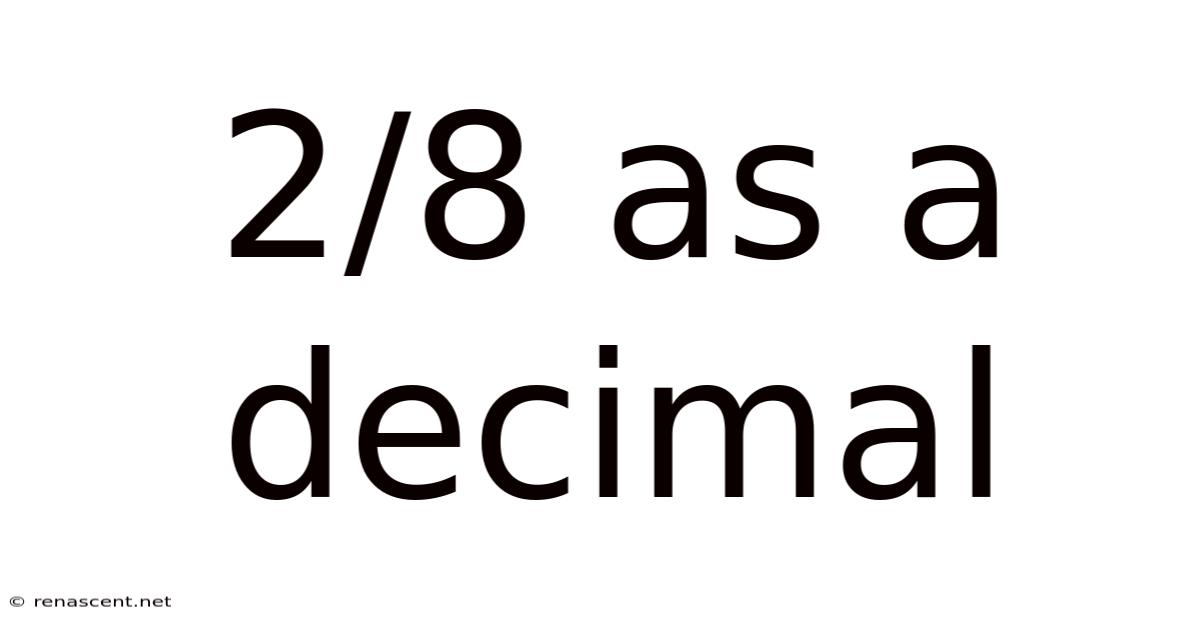
Table of Contents
Unveiling the Decimal Mystery: A Deep Dive into 2/8
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the fraction 2/8 into its decimal form, providing a step-by-step process, explaining the underlying principles, and offering insightful examples to solidify your understanding. We'll go beyond a simple answer, delving into the broader concepts of fractions, decimals, and their interrelationship, making this a valuable resource for students and anyone looking to improve their numeracy skills.
Introduction: Fractions, Decimals, and Their Relationship
Before diving into the specifics of 2/8, let's establish a firm grasp of the basics. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts, and the numerator indicates how many of those parts are being considered.
A decimal, on the other hand, represents a number based on the powers of 10. Each digit to the right of the decimal point represents a decreasing power of 10 (tenths, hundredths, thousandths, and so on). Fractions and decimals are essentially two different ways of expressing the same value. Converting between them is a crucial skill in various mathematical applications.
Method 1: Simplifying the Fraction Before Conversion
The fraction 2/8 can be simplified before converting it to a decimal. Simplification involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 2 and 8 is 2.
Dividing both the numerator and denominator by 2, we get:
2 ÷ 2 / 8 ÷ 2 = 1/4
Now, converting 1/4 to a decimal is much simpler.
Method 2: Direct Division
The most straightforward method to convert a fraction to a decimal is through division. The fraction 2/8 represents the division of 2 by 8. Performing this division gives us:
2 ÷ 8 = 0.25
Therefore, 2/8 is equal to 0.25.
Method 3: Understanding Decimal Place Value
Let's break down the decimal 0.25 to understand its place value. The digit 2 is in the tenths place, representing 2/10. The digit 5 is in the hundredths place, representing 5/100. Adding these together, we get:
2/10 + 5/100 = 20/100 + 5/100 = 25/100
This fraction, 25/100, can be simplified by dividing both the numerator and the denominator by 25, resulting in 1/4, which we've already established is equivalent to 0.25. This reinforces the equivalence of 2/8 and 0.25.
Visual Representation: Understanding the Concept
Imagine a pizza cut into 8 equal slices. The fraction 2/8 represents 2 out of those 8 slices. If you take those 2 slices, you have a portion of the whole pizza. This portion is equivalent to 0.25, or 25% of the entire pizza. Visualizing fractions in this way can help build an intuitive understanding of their decimal equivalents.
Expanding on the Concept: Different Fractions, Similar Approach
Let's apply the same principles to convert other fractions to decimals. Consider the fraction 3/5:
- Direct Division: 3 ÷ 5 = 0.6
- Finding an Equivalent Fraction with a Denominator of a Power of 10: We can multiply both the numerator and denominator by 2 to get 6/10, which is equal to 0.6.
This illustrates the versatility of the methods. You can choose the method most comfortable and efficient for a given fraction.
Dealing with Terminating and Repeating Decimals
Not all fractions convert to neat, terminating decimals like 0.25. Some fractions result in repeating decimals. For example, 1/3 converts to 0.3333..., where the 3 repeats infinitely. Understanding this distinction is crucial in various mathematical contexts. 2/8, however, conveniently results in a terminating decimal.
Practical Applications: Where Decimal Equivalents Matter
The ability to convert fractions to decimals is vital in numerous real-world scenarios:
- Financial calculations: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals.
- Measurement and engineering: Precise measurements frequently require the use of decimals.
- Data analysis: Representing data in decimal form is crucial for statistical analysis and interpretation.
- Computer programming: Many programming tasks necessitate the conversion between fractions and decimals.
Mastering this skill enhances problem-solving abilities in various fields.
Frequently Asked Questions (FAQ)
Q: Is there only one way to convert 2/8 to a decimal?
A: No, as demonstrated, there are several methods. Simplifying the fraction first, direct division, and understanding decimal place value all lead to the same result. Choosing the method depends on personal preference and the complexity of the fraction.
Q: Why is simplifying the fraction beneficial?
A: Simplifying makes the division process easier and less prone to errors. Working with smaller numbers simplifies calculations.
Q: What if the fraction results in a repeating decimal?
A: Repeating decimals can be expressed using a bar notation (e.g., 0.3̅3̅) to indicate the repeating digits. In some contexts, you might round the decimal to a specific number of decimal places.
Q: Can all fractions be converted to decimals?
A: Yes, every fraction can be converted to a decimal through division. The result might be a terminating or a repeating decimal.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals is a core mathematical skill with wide-ranging applications. This guide has comprehensively explored the conversion of 2/8 to its decimal equivalent (0.25), outlining multiple methods and emphasizing the underlying principles. Understanding fractions, decimals, and their interrelationship empowers you to tackle more complex mathematical challenges with confidence. By practicing these methods and exploring various fractions, you can solidify your understanding and build a strong foundation in numeracy. Remember, consistent practice is key to mastering this essential skill. The ability to seamlessly transition between fractions and decimals is a significant step towards achieving mathematical fluency.
Latest Posts
Latest Posts
-
Ac Manifold Gauge Set
Sep 16, 2025
-
2 3as A Percentage
Sep 16, 2025
-
38 8977 N 77 0365 W
Sep 16, 2025
-
27x11 4 Bicycle Tires
Sep 16, 2025
-
1 5 Cm In Mm
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.