2 Square Root X
renascent
Sep 24, 2025 · 6 min read
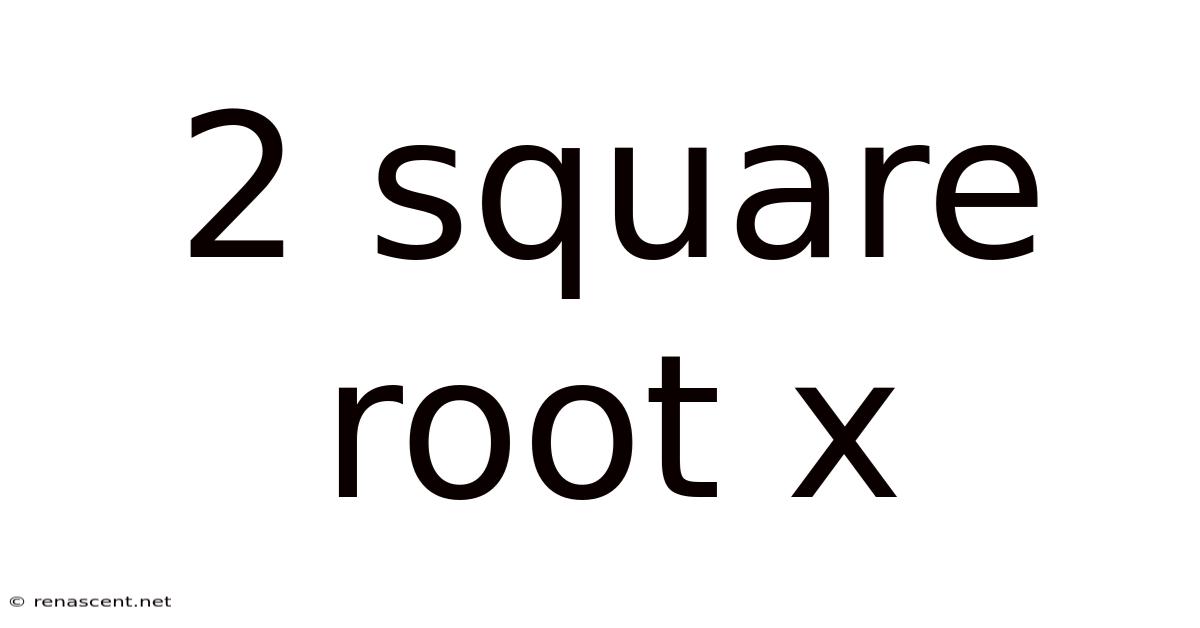
Table of Contents
Decoding the Mystery: A Deep Dive into 2√x
Understanding the mathematical expression "2√x" might seem straightforward at first glance, but a deeper exploration reveals a fascinating interplay of concepts within algebra, calculus, and even geometry. This article will serve as a comprehensive guide, demystifying 2√x, exploring its properties, applications, and implications. We'll move beyond simple calculations and delve into the underlying mathematical principles, ensuring a thorough understanding for readers of all levels.
Introduction: Understanding the Fundamentals
The expression "2√x" represents a number, derived by performing two distinct mathematical operations:
-
Square Root (√x): This operation finds a number that, when multiplied by itself, equals x. For example, √9 = 3 because 3 * 3 = 9. It's crucial to remember that the square root of a number can be positive or negative, though conventionally, the principal square root (the positive value) is used unless otherwise specified.
-
Multiplication by 2: This simply means multiplying the result of the square root operation by 2.
Therefore, 2√x means "twice the square root of x." The value of this expression depends entirely on the value of x. If x is a perfect square (like 9, 16, 25), the calculation is straightforward. If x is not a perfect square, the result will be an irrational number – a number that cannot be expressed as a simple fraction.
Exploring Different Values of x
Let's examine how the expression behaves with different values of x:
- x = 0: 2√0 = 2 * 0 = 0
- x = 1: 2√1 = 2 * 1 = 2
- x = 4: 2√4 = 2 * 2 = 4
- x = 9: 2√9 = 2 * 3 = 6
- x = 16: 2√16 = 2 * 4 = 8
- x = 25: 2√25 = 2 * 5 = 10
- x = 2: 2√2 ≈ 2 * 1.414 = 2.828 (an irrational number)
- x = -1: 2√-1 = 2i (where 'i' is the imaginary unit, √-1)
This simple exploration highlights the diverse outcomes depending on whether 'x' is a perfect square, a non-perfect square, or even a negative number, introducing the concept of complex numbers.
Graphical Representation and Domain
The expression 2√x can be effectively visualized through a graph. The graph of y = 2√x is a curve that starts at the origin (0,0) and increases steadily as x increases. This demonstrates that the function is only defined for non-negative values of x (x ≥ 0). The negative square root is typically excluded from the basic graph but is a valid mathematical consideration. This restricted domain is a direct consequence of the square root operation, as the square root of a negative number is not a real number.
Applications of 2√x in Various Fields
The simplicity of 2√x belies its importance across several branches of mathematics and applied sciences:
-
Geometry: The expression frequently appears in geometric calculations involving areas and lengths. For instance, the diagonal of a square with side length 'x' is given by x√2. Multiplying this by 2 would give you twice the diagonal length.
-
Physics: Many physical phenomena involve square root relationships. For example, the velocity of a wave might be proportional to the square root of a certain parameter. Multiplying by 2 would then double the calculated velocity.
-
Engineering: Calculations of stress, strain, and other mechanical properties often involve square roots. Scaling these results by a factor of 2 would have significant implications in structural design and material science.
-
Finance: In some financial models, growth or decay rates may be expressed with square root functions, often requiring multiplication by a constant factor for accurate prediction.
-
Statistics: In statistical analysis, especially when dealing with distributions and standard deviations, the square root operation frequently occurs, and scaling those results is often necessary.
Calculus and its implications on 2√x
The expression 2√x lends itself well to calculus operations.
-
Differentiation: The derivative of 2√x (or 2x<sup>1/2</sup>) with respect to x is found using the power rule of differentiation: d(2x<sup>1/2</sup>)/dx = x<sup>-1/2</sup> = 1/√x. This derivative represents the instantaneous rate of change of the function 2√x at any given point.
-
Integration: The indefinite integral of 2√x is found using the power rule of integration: ∫2√x dx = (4/3)x<sup>3/2</sup> + C (where C is the constant of integration). This integral represents the area under the curve of y = 2√x.
The ability to differentiate and integrate 2√x makes it useful in solving problems related to optimization, area calculation, and rates of change in various scientific and engineering applications.
Expanding Understanding: Beyond the Basics
Let's further extend our comprehension by looking at more complex variations and related concepts.
-
Transformations: Consider the function y = 2√(x + a) + b. This introduces horizontal and vertical shifts to the basic function y = 2√x. The value 'a' shifts the graph horizontally, while 'b' shifts it vertically. Understanding these transformations is key to interpreting variations of the expression.
-
Inequalities: Solving inequalities involving 2√x requires careful consideration of the domain and the behavior of the square root function. For instance, solving 2√x > 4 requires isolating √x and considering the domain restrictions.
-
Equations: Solving equations involving 2√x often requires squaring both sides of the equation to eliminate the square root, remembering to check for extraneous solutions introduced by the squaring process.
Frequently Asked Questions (FAQ)
-
Q: What is the domain of 2√x?
A: The domain of 2√x is all non-negative real numbers, x ≥ 0. The square root of a negative number is not a real number.
-
Q: Is 2√x always a positive number?
A: Yes, for real values of x, 2√x will always be either zero or a positive number. This is because the principal square root is always non-negative.
-
Q: How do I solve an equation containing 2√x?
A: Isolating the square root term is the first step. Then, square both sides of the equation to eliminate the square root. Remember to check your solution by substituting it back into the original equation to ensure it is valid and not extraneous (a solution that arises during the solving process but does not satisfy the original equation).
-
Q: What is the difference between 2√x and √(2x)?
A: While they might look similar, they are distinct expressions. 2√x means twice the square root of x, while √(2x) means the square root of twice x. Their numerical values will differ, except when x = 0.
-
Q: Can 2√x be negative?
A: If we consider the negative square root, then yes, 2√x can be negative (if x is positive). However, conventionally and in most contexts, only the principal (positive) square root is used.
Conclusion: A Deeper Appreciation of 2√x
This exploration of 2√x has gone beyond simple calculation to uncover its rich mathematical properties and diverse applications. From its graphical representation to its use in calculus and beyond, the expression demonstrates the fundamental importance of seemingly simple mathematical concepts. Understanding its behavior, domain, and implications provides a solid foundation for tackling more complex mathematical problems in various fields. By grasping the nuances of 2√x, we enhance our overall understanding of algebra, calculus, and their practical applications in the world around us. This journey highlights the power of seemingly simple mathematical expressions and their far-reaching influence. It underscores the importance of consistent learning and exploring the depths of mathematical concepts to fully appreciate their power and utility.
Latest Posts
Latest Posts
-
Dynamic Vs Static Equilibrium
Sep 24, 2025
-
75 Percent Of 60
Sep 24, 2025
-
102 Celsius To Fahrenheit
Sep 24, 2025
-
157 Pounds In Kilograms
Sep 24, 2025
-
Certificates Of Deposit Australia
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2 Square Root X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.