75 Percent Of 60
renascent
Sep 24, 2025 · 5 min read
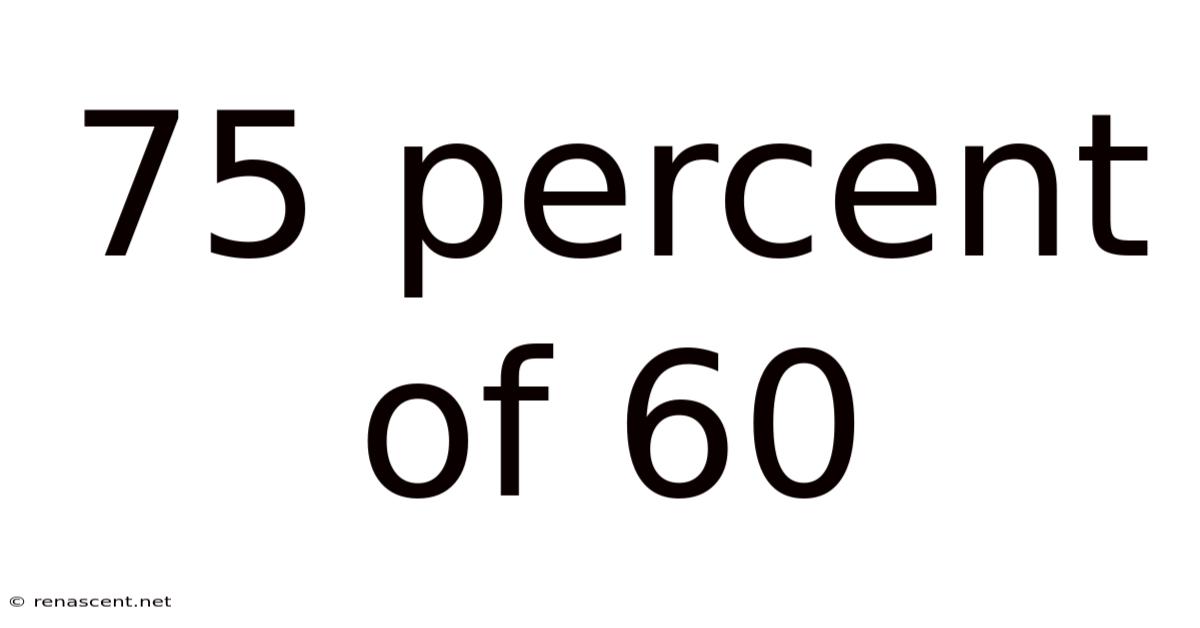
Table of Contents
Decoding 75% of 60: A Comprehensive Guide to Percentages and Applications
Finding 75% of 60 might seem like a simple arithmetic problem, but understanding the underlying concepts unlocks a world of practical applications in various fields. This comprehensive guide will not only show you how to calculate 75% of 60 but will also delve into the broader understanding of percentages, their diverse applications, and some common misconceptions. This detailed explanation will equip you with the skills to tackle similar percentage problems with confidence.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "out of one hundred" ( per cent). Therefore, 75% means 75 out of 100, which can be written as the fraction 75/100 or the decimal 0.75. Understanding this fundamental relationship is key to solving percentage problems.
Method 1: Converting to a Fraction
The most straightforward approach to finding 75% of 60 involves converting the percentage to a fraction. As mentioned above, 75% is equivalent to 75/100. To find 75% of 60, we multiply 60 by the fraction 75/100:
60 x (75/100) = (60 x 75) / 100 = 4500 / 100 = 45
Therefore, 75% of 60 is 45.
This method is particularly useful for mental calculations, especially when dealing with easily simplified fractions. For example, 75/100 simplifies to 3/4, making the calculation even quicker:
60 x (3/4) = (60 x 3) / 4 = 180 / 4 = 45
Method 2: Converting to a Decimal
Another common method involves converting the percentage to a decimal. To do this, we divide the percentage by 100. 75% divided by 100 is 0.75. Then, we multiply 60 by 0.75:
60 x 0.75 = 45
This method is efficient when using calculators, as it avoids dealing with fractions. It's also very useful when working with more complex percentages or when dealing with percentage increase or decrease calculations.
Method 3: Using Proportions
The concept of proportions offers a more formal and adaptable method for solving percentage problems. We can set up a proportion:
x / 60 = 75 / 100
Where x represents the unknown value (75% of 60). To solve for x, we cross-multiply:
100x = 60 x 75
100x = 4500
x = 4500 / 100
x = 45
This method highlights the relationship between the percentage, the whole (60), and the part (45). It's a powerful tool that can be applied to a wide array of percentage problems, even those involving unknown percentages or wholes.
Real-World Applications of Percentages
Understanding percentages is crucial in numerous real-world scenarios:
-
Finance: Calculating interest on loans, savings accounts, and investments relies heavily on percentages. Understanding interest rates and compound interest requires a solid grasp of percentage calculations. For example, if you invest $60 and earn a 75% return, you would have $105. This knowledge is vital for making informed financial decisions.
-
Sales and Discounts: Sales and discounts are often expressed as percentages. Calculating the final price after a discount requires determining the percentage reduction and applying it to the original price. For example, a 75% discount on a $60 item would reduce the price to $15 (60 - (60 * 0.75) = 15).
-
Statistics and Data Analysis: Percentages are frequently used to represent data and express proportions. Understanding percentages is fundamental to interpreting data presented in graphs, charts, and reports. For example, if 75% of surveyed students prefer online learning, this indicates a strong preference for online learning.
-
Science and Engineering: Percentages play a significant role in expressing concentrations, efficiencies, and error margins in scientific and engineering calculations. For instance, expressing the concentration of a solution or the efficiency of a machine often involves percentages.
-
Everyday Life: Calculating tips in restaurants, understanding sales tax, or determining the percentage of a task completed all involve applying the principles of percentage calculations.
Addressing Common Misconceptions
Several common misconceptions surround percentage calculations:
-
Adding percentages directly: A common mistake is to add percentages directly without considering the base value. For example, a 25% increase followed by a 25% decrease does not result in the original value. The base value changes after each percentage adjustment.
-
Misinterpreting percentage changes: Percentage increases and decreases are relative to the initial value. A 10% increase on $100 is different from a 10% increase on $1000.
Frequently Asked Questions (FAQ)
Q: How do I calculate a different percentage of 60?
A: Follow the same methods outlined above, substituting the desired percentage for 75%. For example, to find 20% of 60, you would calculate 60 x (20/100) or 60 x 0.20, which equals 12.
Q: What if the percentage is greater than 100%?
A: If the percentage is greater than 100%, the result will be larger than the original number. For example, 150% of 60 is 60 x (150/100) or 60 x 1.50 = 90. This represents an increase of 50% over the original value.
Q: Can I use a calculator for these calculations?
A: Absolutely! Calculators are particularly helpful for more complex percentage calculations, and they significantly speed up the process.
Q: Are there other ways to solve percentage problems?
A: Yes, there are advanced techniques and formulas, particularly useful in algebra and calculus, but the methods described here are fundamental and broadly applicable.
Conclusion
Calculating 75% of 60, while seemingly simple, serves as a gateway to understanding the broader concept of percentages and their widespread applications. Mastering percentage calculations enhances problem-solving skills across various disciplines, from finance and statistics to everyday life decisions. By understanding the different methods—converting to fractions, decimals, or using proportions—you equip yourself with the tools to tackle a wide range of percentage-related problems with confidence and accuracy. Remember the core principle: a percentage is simply a fraction of 100. With this understanding, the seemingly daunting world of percentages becomes much more manageable and even enjoyable to explore.
Latest Posts
Latest Posts
-
Eastern Hills Basketball Association
Sep 24, 2025
-
Disadvantages Of Electron Microscope
Sep 24, 2025
-
5 Of 10 Million
Sep 24, 2025
-
4 Out Of 16
Sep 24, 2025
-
Boiling Point Of Silver
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 75 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.