20/3 As A Decimal
renascent
Sep 25, 2025 · 6 min read
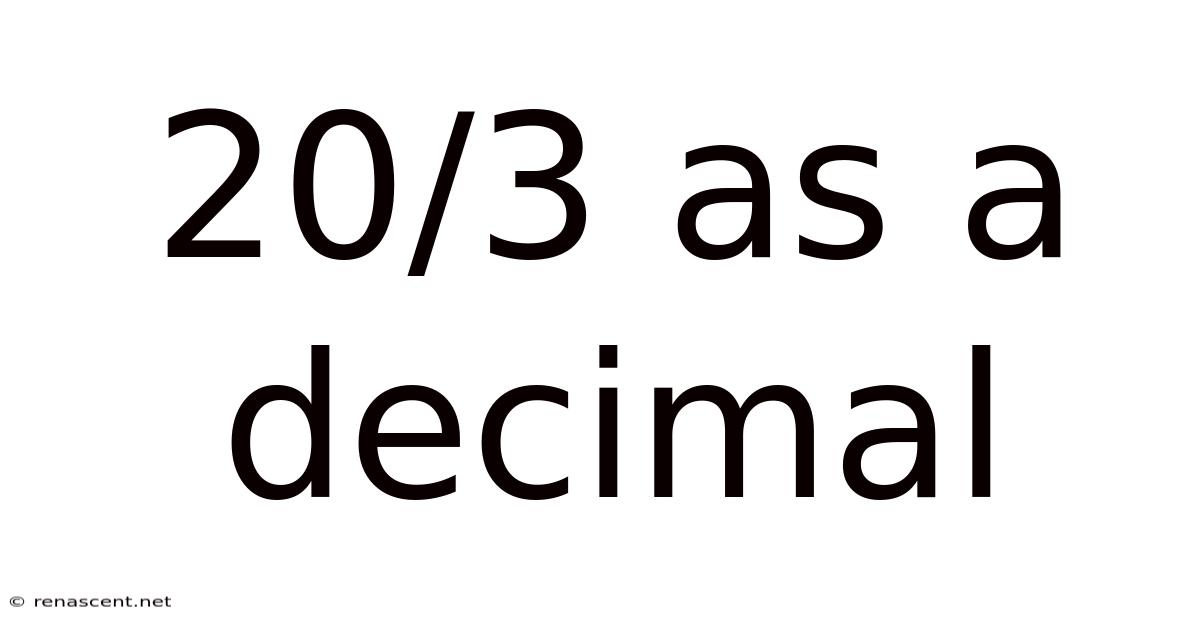
Table of Contents
Decoding 20/3: A Deep Dive into Decimal Conversion and its Applications
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the fraction 20/3 into its decimal form, delving into the methods involved, the resulting decimal's properties, and its practical applications in various fields. We'll cover the basics for beginners, and also explore more advanced concepts for those seeking a deeper understanding. Learn how to confidently convert fractions to decimals and appreciate the power of this mathematical transformation.
Introduction to Fraction-to-Decimal Conversion
Before diving into the specifics of 20/3, let's review the general process of converting a fraction to a decimal. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). To convert a fraction to a decimal, we essentially perform a division: we divide the numerator by the denominator.
For example, the fraction 1/2 can be converted to a decimal by dividing 1 by 2, resulting in 0.5. Similarly, 3/4 becomes 0.75 (3 divided by 4). However, some fractions, like 20/3, produce decimals that are not as straightforward.
Converting 20/3 to a Decimal: The Long Division Method
The most common method for converting a fraction like 20/3 to a decimal is long division. This method involves systematically dividing the numerator (20) by the denominator (3).
-
Set up the division: Write 20 as the dividend (inside the long division symbol) and 3 as the divisor (outside).
-
Divide: 3 goes into 20 six times (3 x 6 = 18). Write the 6 above the 20.
-
Subtract: Subtract 18 from 20, leaving a remainder of 2.
-
Add a decimal point and a zero: Since we have a remainder, add a decimal point to the quotient (the number above the division symbol) and a zero to the remainder. This allows us to continue the division process.
-
Bring down the zero: Bring down the zero next to the remainder 2, making it 20.
-
Repeat: Now divide 20 by 3 again. 3 goes into 20 six times (3 x 6 = 18). Write the 6 after the decimal point in the quotient.
-
Subtract again: Subtract 18 from 20, resulting in a remainder of 2.
-
Repeating Decimal: Notice that the remainder is 2 again. This means the division will continue infinitely, with the digit 6 repeating indefinitely.
Therefore, 20/3 as a decimal is 6.6666..., often written as 6.6̅ (the bar over the 6 indicates that it repeats infinitely). This is an example of a repeating decimal or recurring decimal.
Understanding Repeating Decimals
Repeating decimals are decimals where one or more digits repeat infinitely. They arise when the division process in fraction-to-decimal conversion doesn't terminate. Instead of ending with a remainder of 0, the remainder repeats a sequence, leading to a repeating pattern in the decimal representation.
It's important to understand that repeating decimals are perfectly valid numbers. They represent precise values, even though their decimal representation extends infinitely. Mathematical tools exist to perform calculations and manipulations with repeating decimals accurately.
Alternative Methods for Conversion
While long division is the most common method, other approaches can also be used to convert 20/3 to a decimal. These include using a calculator (which will usually show a truncated or rounded version of the repeating decimal) and employing techniques based on understanding the relationship between fractions and decimals.
Practical Applications of 20/3 and its Decimal Equivalent
The fraction 20/3 and its decimal equivalent, 6.6̅, appear in various contexts within mathematics and its applications:
-
Measurement and Engineering: In engineering and construction, measurements might involve fractions and require conversion to decimals for calculations. Imagine calculating the length of a beam where a dimension is expressed as 20/3 meters; converting this to approximately 6.67 meters is crucial for precise measurements.
-
Finance and Accounting: Calculations involving shares, profits, and losses often involve fractions. Converting these fractions to decimals simplifies financial calculations and reporting.
-
Data Analysis and Statistics: Data sets often contain fractional values. Converting these fractions to decimals is necessary for statistical analysis and interpretation. For example, if the average number of items sold per day is 20/3, converting it to a decimal helps understand the daily sales trend more clearly.
-
Computer Programming: Computer programs frequently handle both integers and floating-point numbers (decimals). Converting a fraction to a decimal is essential for programming algorithms involving fractions or ratios.
-
Everyday Life: While less frequent than in technical fields, situations arise where converting 20/3 to a decimal is useful. For example, splitting a bill of 20 units amongst 3 people requires calculating 20/3 = 6.67 units per person.
Rounding Repeating Decimals
Since repeating decimals extend infinitely, we often need to round them to a specific number of decimal places for practical applications. Rounding involves approximating the value to a certain level of precision. For instance, 6.6̅ can be rounded to:
- 6.7 (rounded to one decimal place)
- 6.67 (rounded to two decimal places)
- 6.667 (rounded to three decimal places)
The level of precision required depends on the context. In engineering applications, a higher level of precision might be necessary, while in everyday calculations, rounding to one or two decimal places might suffice.
FAQs about Decimal Conversion
Q1: Why does 20/3 result in a repeating decimal?
A1: A fraction results in a repeating decimal when the denominator contains prime factors other than 2 and 5. The denominator of 20/3 is 3, a prime factor not equal to 2 or 5, leading to a repeating decimal.
Q2: Is there a way to express 20/3 as a non-repeating decimal?
A2: No, 20/3 cannot be expressed as a non-repeating decimal. Its decimal representation will always be 6.6̅.
Q3: How accurate is rounding a repeating decimal?
A3: The accuracy of rounding a repeating decimal depends on the number of decimal places retained. The more decimal places, the more accurate the approximation, but it's still an approximation, not the exact value.
Q4: Can all fractions be converted to decimals?
A4: Yes, all fractions can be converted to decimals. Some will result in terminating decimals (decimals with a finite number of digits), while others will result in repeating decimals.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals is a crucial skill applicable across various fields. Understanding the process, particularly with fractions like 20/3 which result in repeating decimals, empowers you to handle mathematical problems with greater confidence and accuracy. Remember that while repeating decimals seem complex, they represent precise values and can be handled effectively with appropriate methods, such as long division, calculators, and rounding techniques, depending on the level of precision needed for a specific application. The mastery of this conversion enhances your understanding of numbers and their diverse representations, solidifying your foundational mathematical skills.
Latest Posts
Latest Posts
-
3 55 Kg To Pounds
Sep 25, 2025
-
163 Pounds To Kg
Sep 25, 2025
-
32 8 Ft To Meters
Sep 25, 2025
-
Pink Blue Mix Color
Sep 25, 2025
-
Back To Back Stemplot
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 20/3 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.