20/35 As A Percent
renascent
Sep 24, 2025 · 5 min read
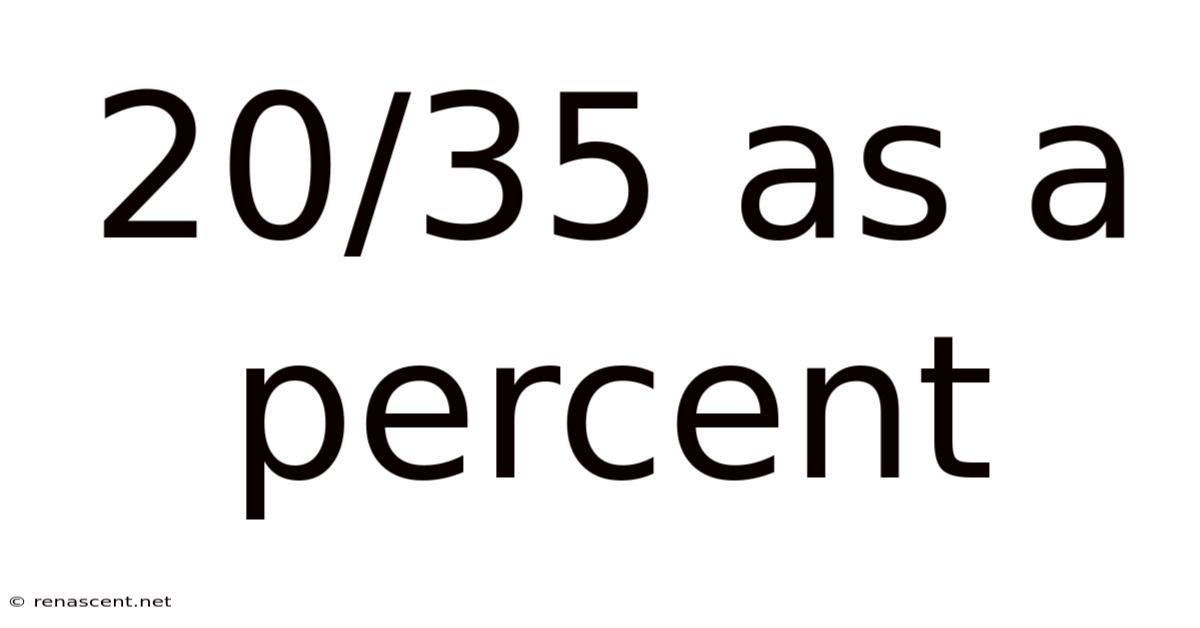
Table of Contents
20/35 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from everyday budgeting to advanced scientific calculations. This comprehensive guide will delve into the process of converting the fraction 20/35 into a percentage, providing a step-by-step explanation, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll also examine the broader context of fraction-to-percentage conversions and their practical significance.
Understanding Fractions and Percentages
Before diving into the specific conversion of 20/35, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, in the fraction 20/35, 20 is the numerator and 35 is the denominator. This signifies that we have 20 parts out of a total of 35 parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts out of 100 constitute a given portion. For instance, 50% signifies 50 parts out of 100, which is equivalent to one-half (1/2). Percentages are widely used because they provide a standardized and easily understandable way to express proportions.
Converting 20/35 to a Percentage: A Step-by-Step Approach
The conversion of a fraction to a percentage involves two primary steps:
Step 1: Convert the fraction to a decimal.
To do this, we divide the numerator (20) by the denominator (35):
20 ÷ 35 = 0.57142857...
The result is a decimal number. Note that this decimal may be recurring (like in this case), meaning the digits repeat infinitely. For practical purposes, we often round the decimal to a desired number of decimal places.
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.57142857... × 100 ≈ 57.14%
Therefore, 20/35 is approximately equal to 57.14%. The approximation arises from rounding the decimal value. Depending on the context, you may choose to round to a different number of decimal places (e.g., 57.1%, 57%).
Simplifying the Fraction Before Conversion
Before performing the division, it's often beneficial to simplify the fraction if possible. This simplifies the calculation and reduces the risk of errors. Both 20 and 35 are divisible by 5:
20 ÷ 5 = 4 35 ÷ 5 = 7
So, 20/35 simplifies to 4/7. Now, we can convert 4/7 to a decimal and then a percentage:
4 ÷ 7 ≈ 0.5714
0.5714 × 100 ≈ 57.14%
This yields the same result, but the calculation is simpler using the simplified fraction.
Mathematical Principles Behind the Conversion
The conversion from a fraction to a percentage relies on the fundamental concept of proportions. A percentage is simply a fraction with a denominator of 100. Therefore, converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100. This can be achieved by multiplying both the numerator and the denominator of the original fraction by a factor that results in a denominator of 100.
However, this method isn't always practical, especially when the denominator isn't a simple factor of 100. The more efficient approach, as demonstrated above, involves converting the fraction to a decimal first, which effectively performs the proportional scaling implicitly. Multiplying the decimal by 100 then directly gives the percentage.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Financial calculations: Determining interest rates, calculating discounts, analyzing profit margins, and understanding financial statements all involve working with percentages.
-
Statistics and data analysis: Percentages are used extensively to represent proportions within datasets, facilitating comparisons and interpretations of data.
-
Scientific measurements and experiments: Expressing experimental results as percentages helps to standardize and easily compare findings.
-
Everyday life: Calculating tips, understanding sales tax, and determining proportions in recipes all utilize percentage calculations.
Frequently Asked Questions (FAQs)
-
Q: What if the decimal representation of the fraction is non-terminating and non-repeating?
*A: In such cases, rounding to a suitable number of decimal places is necessary for practical applications. The level of precision required depends on the context.
-
Q: Is there a quicker way to convert fractions to percentages?
*A: While the method outlined above is generally reliable and easy to understand, some simple fractions can be quickly converted mentally. For example, 1/2 is 50%, 1/4 is 25%, and 3/4 is 75%.
-
Q: Can I convert a mixed number (e.g., 2 1/2) to a percentage?
*A: Yes, first convert the mixed number into an improper fraction (in this case, 5/2), then follow the steps outlined above to convert the improper fraction to a percentage. 5/2 = 2.5, and 2.5 * 100 = 250%.
-
Q: What are the potential errors to avoid when converting fractions to percentages?
*A: Common errors include incorrect division of the numerator by the denominator, mistakes in multiplying the decimal by 100, and improper rounding. Always double-check your calculations.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with numerous real-world applications. The process involves converting the fraction to a decimal by dividing the numerator by the denominator and then multiplying the decimal by 100 to obtain the percentage. Simplifying the fraction before conversion can often streamline the calculation. Understanding the underlying mathematical principles ensures a deeper comprehension of the conversion process and its significance. Mastering this skill empowers individuals to confidently tackle various numerical challenges across diverse fields. Remember to always double-check your calculations and consider the level of precision needed based on the context of your problem.
Latest Posts
Latest Posts
-
Indigenous Games For Kids
Sep 24, 2025
-
What Are Automatic Stabilisers
Sep 24, 2025
-
750 Ml To Liters
Sep 24, 2025
-
Dynamic Vs Static Equilibrium
Sep 24, 2025
-
75 Percent Of 60
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 20/35 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.