20 Divided By 17
renascent
Sep 19, 2025 · 5 min read
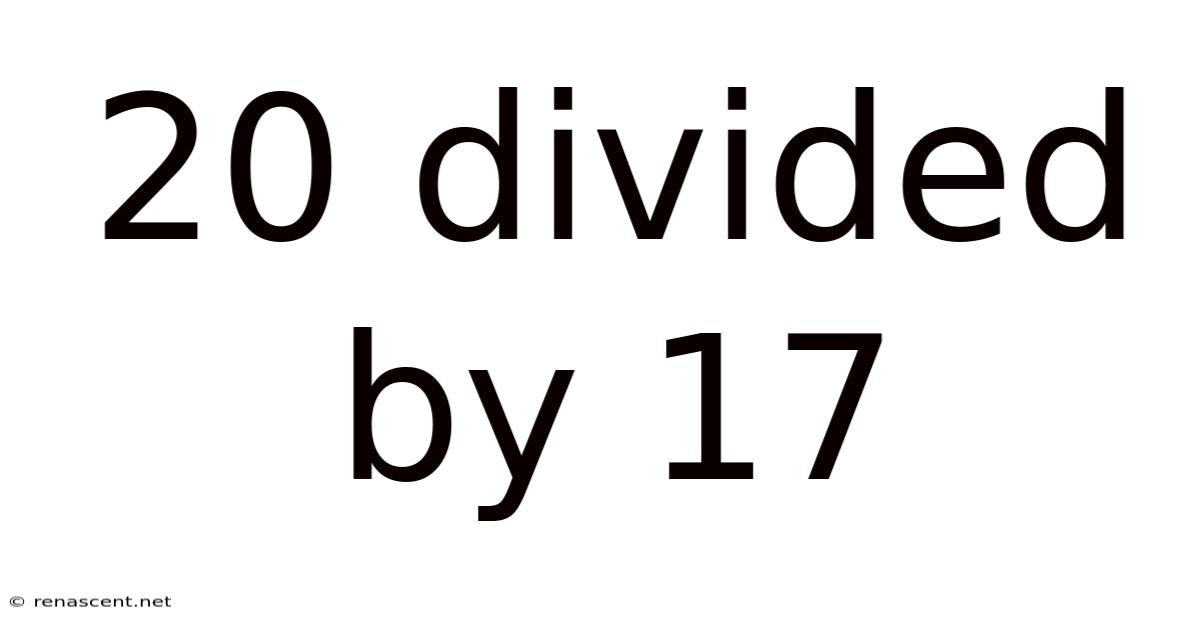
Table of Contents
Exploring the Division: 20 Divided by 17
Dividing 20 by 17 might seem like a simple arithmetic problem, a quick calculation for many. But beneath the surface of this seemingly straightforward equation lies a world of mathematical concepts that are fundamental to understanding numbers and their relationships. This article will delve deep into the division of 20 by 17, exploring its result, its implications in different mathematical contexts, and its applications in real-world scenarios. We will unravel the mystery behind this seemingly simple calculation, revealing the rich mathematical tapestry it represents.
Understanding the Basics: Division and its Components
Before we dive into the specifics of 20 divided by 17, let's revisit the fundamental concepts of division. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity (the dividend) into equal parts, with the number of parts specified by another quantity (the divisor). The result of this division is called the quotient. There might also be a remainder if the dividend is not perfectly divisible by the divisor.
In our case, 20 is the dividend and 17 is the divisor. We are looking for the number of times 17 fits into 20, and any leftover amount.
Calculating 20 Divided by 17: The Quotient and Remainder
Performing the division:
20 ÷ 17 = 1 with a remainder of 3
This means that 17 fits into 20 only once. After subtracting 17 from 20, we are left with a remainder of 3. This can be expressed in several ways:
- As a whole number with a remainder: 1 R 3
- As a mixed number: 1 3/17 (This represents one whole and three seventeenths)
- As a decimal: Approximately 1.1765 (This is a non-terminating, repeating decimal, as we will explore later).
Different Representations: Exploring Decimal and Fractional Forms
The decimal representation of 20/17 is a recurring decimal, meaning the digits after the decimal point repeat infinitely. This is because 17 is not a factor of 10 or any power of 10. Performing long division will reveal the repeating sequence:
1.1764705882352941...
This sequence continues infinitely without a terminating digit. This type of decimal is called a repeating decimal or recurring decimal. The repeating block is "1764705882352941".
The fractional form, 1 3/17, provides an exact representation of the result, avoiding the limitations of decimal approximation. It clearly shows the whole number part (1) and the fractional part (3/17), which represents the remainder.
The Significance of Remainders in Division
The remainder (3, in this case) holds significance in various mathematical applications. For instance, in problems involving modular arithmetic (often used in cryptography and computer science), the remainder is the key piece of information. Modulo operation (represented by the symbol %) finds the remainder after a division. For example, 20 % 17 = 3.
Applying the Division: Real-World Examples
While 20 divided by 17 might not seem immediately applicable to everyday life, it represents a fundamental mathematical operation that underlies many practical scenarios. Consider these examples:
- Distributing items: Imagine you have 20 candies to distribute equally among 17 children. Each child gets one candy, and you have 3 candies left over.
- Resource allocation: If you have 20 meters of fabric and need 17 meters for a project, you'll have 3 meters left for another project.
- Unit conversions: In situations involving conversion between units with uneven relationships, you might encounter remainders, mirroring the concept in 20/17.
- Programming and Algorithms: Remainders are crucial in various computer algorithms, such as those used for hashing, data structures, and simulations.
Delving Deeper: Exploring Continued Fractions
The result of 20/17 can also be expressed as a continued fraction, offering another unique perspective on the division. A continued fraction is an expression that represents a number as a sum of a whole number and the reciprocal of another number, which itself is a sum of a whole number and a reciprocal, and so on. While deriving the continued fraction for 20/17 is more advanced, it demonstrates the multifaceted nature of representing numbers.
Long Division: A Step-by-Step Approach
Let's break down the long division process for 20 divided by 17:
- Set up: Write 20 inside the long division symbol and 17 outside.
- Divide: How many times does 17 go into 20? Only once (1). Write the 1 above the 20.
- Multiply: Multiply the quotient (1) by the divisor (17): 1 x 17 = 17.
- Subtract: Subtract the result (17) from the dividend (20): 20 - 17 = 3.
- Remainder: The result (3) is the remainder.
Therefore, 20 ÷ 17 = 1 with a remainder of 3.
Frequently Asked Questions (FAQ)
- Q: What is the exact decimal value of 20/17? A: There is no exact decimal value, as it is a non-terminating, repeating decimal.
- Q: Can 20/17 be simplified? A: No, 20 and 17 share no common factors other than 1, so the fraction 20/17 is already in its simplest form.
- Q: What are some real-world applications beyond the examples provided? A: Remainders are vital in scheduling, time management, resource allocation in various industries, and many algorithms in computer science.
- Q: How does this relate to other mathematical concepts? A: This division problem connects to concepts like modular arithmetic, continued fractions, number theory, and decimal representation of numbers.
Conclusion: Beyond a Simple Calculation
The seemingly simple division of 20 by 17 opens a window into a wide range of mathematical concepts and practical applications. From the representation of the result as a mixed number, decimal, or continued fraction to its significance in modular arithmetic and real-world problem-solving, this seemingly simple calculation reveals the depth and interconnectedness within the world of mathematics. Understanding this simple division provides a strong foundation for tackling more complex mathematical problems and for appreciating the power and elegance of mathematical principles in everyday life. It emphasizes that even simple calculations hold far-reaching implications and contribute to a deeper understanding of the mathematical universe.
Latest Posts
Latest Posts
-
1128 Minutes To Hours
Sep 19, 2025
-
5 3 Lbs In Kg
Sep 19, 2025
-
54 Months In Years
Sep 19, 2025
-
Romeo And Juliet Essay
Sep 19, 2025
-
10 Percent Of 1000
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 20 Divided By 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.