200 Divided By 30
renascent
Sep 20, 2025 · 6 min read
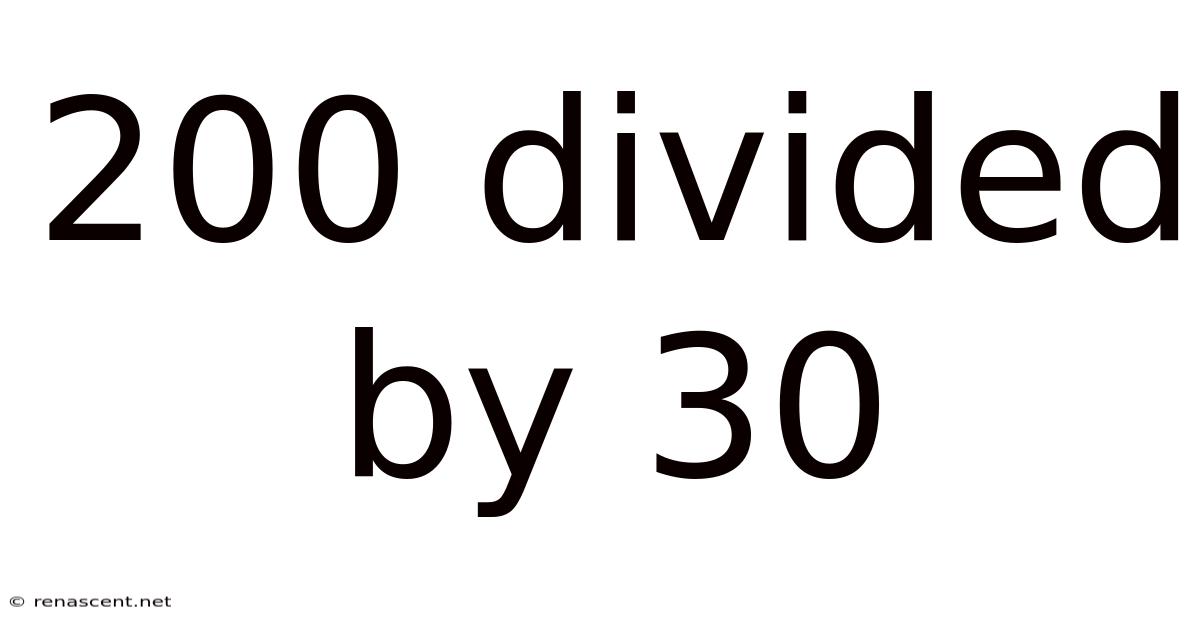
Table of Contents
200 Divided by 30: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 200 divided by 30, delving far beyond the basic answer. We'll uncover the underlying principles of division, explore various methods for solving this problem, examine its practical applications, and discuss related mathematical concepts. Understanding this seemingly simple division problem provides a strong foundation for more complex mathematical concepts. This guide is perfect for students needing a refresher, or anyone looking to improve their understanding of arithmetic and its real-world uses.
Introduction: Understanding Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially represents the process of splitting a quantity into equal parts. In the context of 200 divided by 30 (written as 200 ÷ 30 or 200/30), we're asking: "How many times does 30 fit into 200?"
The answer isn't a whole number; division often results in a quotient (the whole number result) and a remainder (the amount left over). This leads us to explore different ways of representing the result.
Methods for Solving 200 ÷ 30
Several methods can be used to solve this division problem:
1. Long Division: This traditional method provides a step-by-step process for solving division problems, particularly useful for larger numbers.
- We start by dividing 20 (the tens digit of 200) by 30. 30 doesn't go into 20, so we move to the next digit.
- We now consider 200 as a whole. How many times does 30 fit into 200? We can estimate. 30 x 6 = 180, and 30 x 7 = 210. Since 210 is greater than 200, 6 is our quotient.
- We subtract 180 (6 x 30) from 200, leaving a remainder of 20.
- Therefore, 200 ÷ 30 = 6 with a remainder of 20.
2. Decimal Division: Instead of a remainder, we can express the result as a decimal.
- We perform long division as before, but instead of stopping at the remainder, we add a decimal point and a zero to the dividend (200).
- This becomes 200.0. We continue the division process, bringing down the zero.
- 30 goes into 200 six times (180), leaving 20. We bring down the zero, making it 200.
- 30 goes into 200 six times again (180), leaving 20. This process repeats, resulting in a recurring decimal.
- Therefore, 200 ÷ 30 ≈ 6.666... (the 6 repeats infinitely). We often round this to a certain number of decimal places, for example, 6.67.
3. Fraction Representation: The result can be elegantly expressed as a fraction.
- The result of 200 ÷ 30 is simply the fraction 200/30.
- This fraction can be simplified by finding the greatest common divisor (GCD) of 200 and 30, which is 10.
- Dividing both the numerator and denominator by 10, we get 20/3.
- This is an improper fraction (numerator is larger than the denominator) and can be converted into a mixed number: 6 and 2/3. This shows the quotient (6) and the remainder (2) in a concise form.
Understanding the Remainder
The remainder (20 in this case) represents the portion of the dividend (200) that is not evenly divisible by the divisor (30). It's crucial to understand the context of the problem to interpret the remainder meaningfully.
For instance, if we're dividing 200 candies among 30 children, each child gets 6 candies, and there are 20 candies left over. These remaining candies could be distributed in different ways (e.g., given to a teacher, saved for later, etc.). The context determines how to handle the remainder.
Real-World Applications
The division of 200 by 30 has many practical applications across different fields:
- Resource Allocation: Distributing resources such as budget, materials, or time among groups. For example, dividing $200 among 30 people for a team event.
- Averaging: Calculating average values. Suppose 30 students scored a total of 200 points on a test; the average score is 200/30 ≈ 6.67 points.
- Scaling: Adjusting recipes or plans. A recipe for 30 servings requires 200 grams of flour; how much flour is needed for 1 serving? 200/30 ≈ 6.67 grams.
- Unit Conversion: Converting units of measurement. Imagine needing to convert 200 centimeters into groups of 30 centimeters each.
- Probability and Statistics: In statistical calculations involving proportions or frequencies.
Deeper Mathematical Concepts
This seemingly simple division problem touches upon several important mathematical concepts:
- Divisibility Rules: While there's no specific divisibility rule for 30, understanding divisibility rules for 2, 3, 5, and 10 helps simplify calculations.
- Prime Factorization: Breaking down numbers into their prime factors (200 = 2³ x 5² and 30 = 2 x 3 x 5) can simplify fraction reduction.
- Greatest Common Divisor (GCD): Finding the GCD allows for simplification of fractions, making them easier to understand and work with.
- Least Common Multiple (LCM): The LCM is useful when adding or subtracting fractions.
- Decimal Representation and Recurring Decimals: Understanding how fractions can be represented as decimals, and the nature of recurring decimals, is fundamental to number theory.
- Modular Arithmetic: The remainder in a division problem is central to modular arithmetic, used in cryptography and other advanced mathematical fields.
Frequently Asked Questions (FAQ)
-
Q: What is the exact answer to 200 divided by 30?
- A: The exact answer is 6 with a remainder of 20, or 20/3 as a fraction, or approximately 6.666... as a decimal.
-
Q: How do I handle the remainder in a real-world problem?
- A: The treatment of the remainder depends entirely on the context. Sometimes rounding up or down is appropriate, while other times the remainder represents a leftover quantity that needs separate consideration.
-
Q: Why is the decimal result recurring?
- A: The decimal result (6.666...) is recurring because the fraction 20/3 cannot be expressed as a terminating decimal. This is because the denominator (3) contains prime factors other than 2 and 5.
-
Q: Are there other ways to represent the answer besides decimals and fractions?
- A: Yes, the answer could also be represented visually using diagrams or models, such as dividing 200 objects into groups of 30.
Conclusion: Beyond the Basics
While the basic answer to 200 divided by 30 is seemingly simple, exploring the problem through different methods and relating it to broader mathematical concepts reveals a wealth of knowledge. From understanding long division and decimal representation to grasping the significance of remainders and applying these concepts to real-world scenarios, this seemingly simple calculation provides a springboard for understanding more complex mathematical ideas. The key takeaway is that even fundamental arithmetic operations have depth and practical relevance far beyond the immediate answer. Remember that mathematical understanding is built upon a foundation of these seemingly basic concepts, so mastering them is crucial for advancement in more advanced areas.
Latest Posts
Latest Posts
-
70 Divided By 15
Sep 20, 2025
-
Decomposers Of The Desert
Sep 20, 2025
-
0 55 As A Fraction
Sep 20, 2025
-
44 Kg In Stones
Sep 20, 2025
-
609 Divided By 21
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 200 Divided By 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.