70 Divided By 15
renascent
Sep 20, 2025 · 5 min read
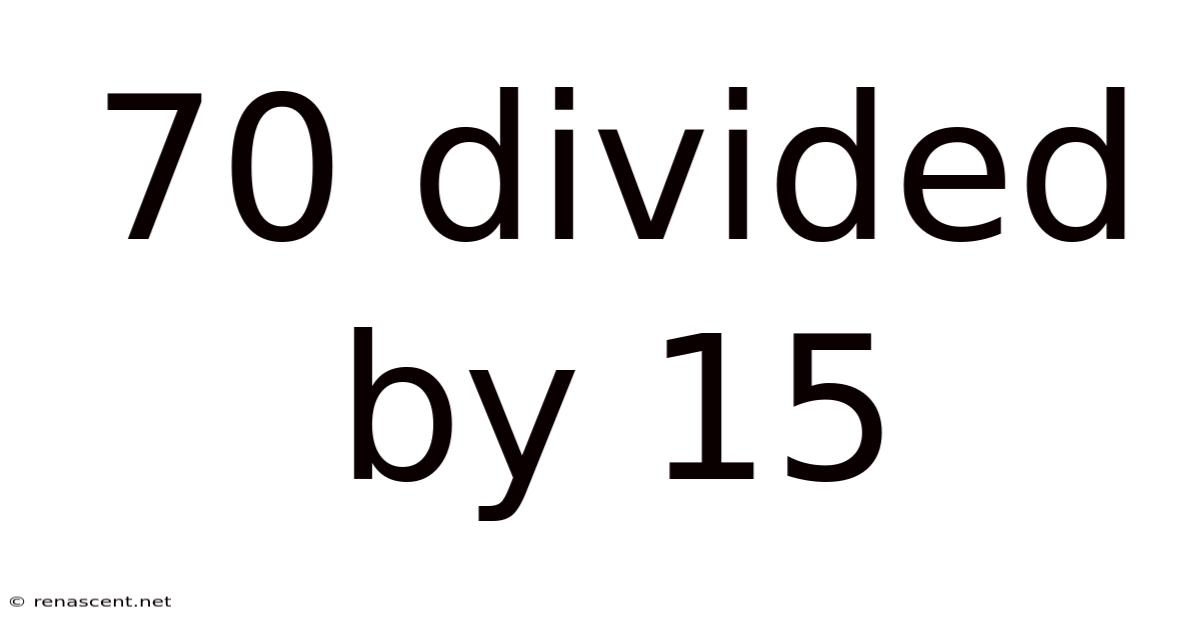
Table of Contents
70 Divided by 15: A Deep Dive into Division and its Applications
Dividing 70 by 15 might seem like a simple arithmetic problem, but it offers a fascinating entry point into understanding the broader concepts of division, fractions, decimals, and their real-world applications. This article will not only provide the solution but also explore the various methods for solving this problem and delve into the underlying mathematical principles. We'll also touch upon practical examples showcasing the relevance of division in everyday life.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. In the context of 70 divided by 15 (written as 70 ÷ 15 or 70/15), we're asking: "How many times does 15 fit into 70?"
Methods for Solving 70 ÷ 15
There are several approaches to solve this division problem:
- Long Division: This is a traditional method, especially useful for larger numbers.
4
15 | 70
-60
10
The result is 4 with a remainder of 10. This means 15 goes into 70 four times, with 10 left over.
- Fraction Representation: We can express 70 ÷ 15 as the fraction 70/15. This fraction can be simplified by finding the greatest common divisor (GCD) of 70 and 15, which is 5. Dividing both the numerator and the denominator by 5 gives us:
70/15 = (70 ÷ 5) / (15 ÷ 5) = 14/3
This simplified fraction represents the exact answer.
- Decimal Representation: To express the answer as a decimal, we can perform long division further:
4.666...
3 | 14.000
-12
20
-18
20
-18
2...
The result is 4.666..., which is a repeating decimal. This is because 14/3 is a rational number with a denominator that is not a power of 10.
Interpreting the Results
Each method provides a slightly different perspective on the answer:
-
4 with a remainder of 10: This is useful when dealing with discrete objects. Imagine you have 70 apples and want to put them into bags of 15. You can fill 4 bags completely, and you'll have 10 apples left over.
-
14/3: This is the exact mathematical representation. It's a precise answer, useful in calculations where approximations are undesirable.
-
4.666...: This is a decimal approximation, convenient for everyday calculations or when dealing with quantities that can be subdivided (e.g., 70 liters of liquid divided into containers of 15 liters each). The repeating decimal indicates that the division is not exact.
Understanding Remainders and Their Significance
The remainder in the long division (10) holds significant meaning. It represents the portion of the dividend (70) that is left over after the divisor (15) has been applied as many times as possible without exceeding the dividend. The remainder’s interpretation depends on the context of the problem. In some cases, it might be discarded (e.g., rounding down the number of bags needed). In other instances, it needs to be considered (e.g., you need an extra bag for the remaining apples).
Real-World Applications of Division
Division is a fundamental mathematical operation that finds application across a wide range of fields and everyday situations:
-
Sharing and Distribution: Dividing resources fairly among individuals or groups (e.g., sharing cookies, splitting a bill, distributing workload).
-
Measurement and Conversion: Converting units of measurement (e.g., converting kilometers to miles, meters to feet).
-
Rate and Ratio Problems: Calculating speeds, unit prices, or proportions (e.g., miles per hour, cost per item, parts per million).
-
Finance and Budgeting: Dividing income to allocate funds for different expenses (e.g., calculating monthly installments, determining profit margins).
-
Geometry and Area Calculations: Calculating area of shapes based on dimensions (e.g., finding the area of a rectangle using length and width).
Advanced Concepts: Fractions and Decimals
The problem of 70 ÷ 15 seamlessly integrates concepts of fractions and decimals. The simplified fraction 14/3 highlights the relationship between division and fractions. Any division problem can be represented as a fraction, with the dividend as the numerator and the divisor as the denominator. Conversely, any fraction can be interpreted as a division problem.
Decimals, on the other hand, provide an alternative way to represent fractions, particularly useful when dealing with approximations and continuous quantities. The repeating decimal 4.666... is a testament to the fact that some fractions cannot be expressed exactly as finite decimals.
Practical Examples
Let's consider some real-world scenarios where understanding 70 ÷ 15 becomes essential:
-
Baking: If you have 70 grams of flour and need 15 grams for each cookie, you can make 4 cookies with 10 grams of flour left over.
-
Packaging: You have 70 candies to pack into bags of 15 candies each. You can fill 4 bags completely, leaving 10 candies for a smaller bag or to be added to the next batch.
-
Manufacturing: A machine produces 70 units per hour, and each unit takes 15 minutes to assemble. The machine can complete 4 units per hour (60 minutes/ 15 minutes per unit = 4 units).
-
Resource Allocation: A team of 15 people needs to complete a project in 70 hours. Each team member is allocated approximately 4.67 hours (70 hours / 15 people ≈ 4.67 hours/person).
Frequently Asked Questions (FAQ)
-
What is the exact answer to 70 divided by 15? The exact answer is 14/3 or 4 with a remainder of 10.
-
Why is the decimal answer a repeating decimal? Because the fraction 14/3 is a rational number whose denominator (3) is not a power of 10.
-
How do I choose between using the fraction, decimal, or remainder-based answer? The best approach depends on the context of the problem. Fractions provide precision, decimals offer convenience for approximations, and remainders are useful for dealing with discrete, indivisible quantities.
-
Can I use a calculator to solve this? Yes, a calculator will give you the decimal approximation (4.666...).
Conclusion
Solving 70 divided by 15, seemingly a simple calculation, opens up a vast realm of mathematical concepts and their real-world applications. Understanding the different methods of solving this problem – long division, fraction representation, and decimal representation – provides a strong foundation for tackling more complex division problems and strengthens our comprehension of fractions, decimals, and remainders. The ability to interpret results in various contexts empowers problem-solving skills in diverse situations, from simple everyday tasks to more intricate scientific or engineering calculations. The key takeaway is that understanding the 'why' behind the 'how' is just as important as obtaining the numerical answer itself.
Latest Posts
Latest Posts
-
15 3 Cm To Inches
Sep 20, 2025
-
Katniss Everdeen Fire Dress
Sep 20, 2025
-
Inch Of Gold Usa
Sep 20, 2025
-
Spiritual Meaning Of Sneezes
Sep 20, 2025
-
75 In A Decimal
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 70 Divided By 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.