21/40 As A Percentage
renascent
Sep 14, 2025 · 5 min read
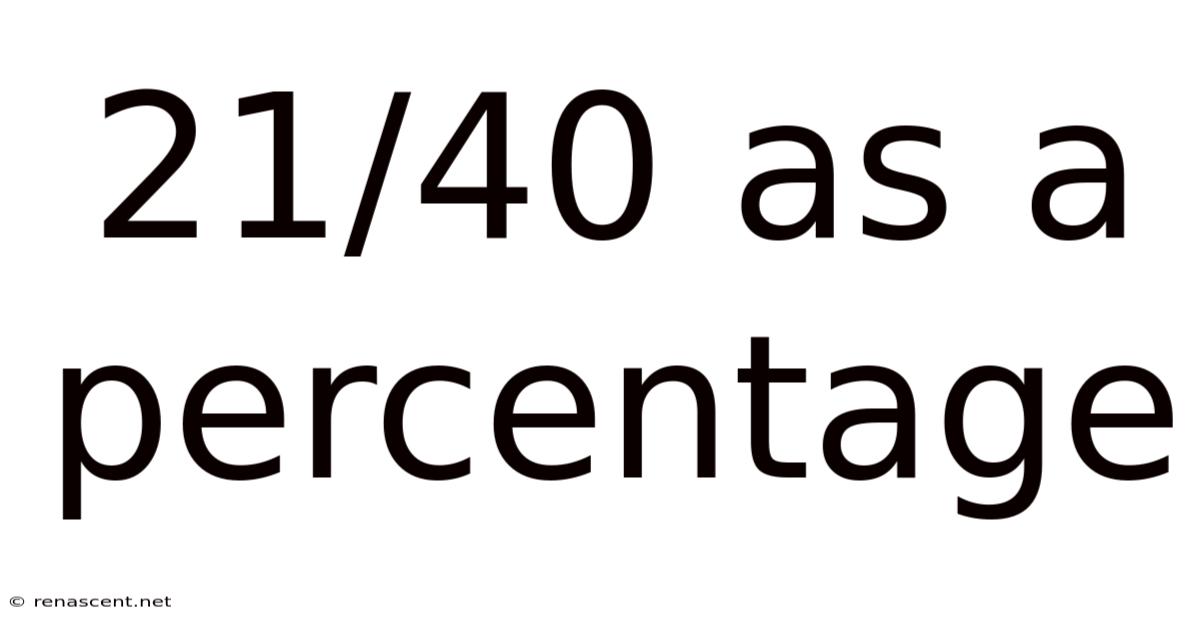
Table of Contents
21/40 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This article delves deep into converting the fraction 21/40 into a percentage, explaining the process step-by-step, providing context, and exploring related concepts. We'll uncover the underlying principles, tackle common misconceptions, and equip you with the knowledge to confidently handle similar conversions. This comprehensive guide ensures you not only understand how to convert 21/40 to a percentage but also why the method works.
Introduction: Fractions, Decimals, and Percentages – A Unified System
Before we jump into the conversion of 21/40, let's establish a clear understanding of the interconnectedness of fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fractions: Express a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 21/40 represents 21 parts out of a total of 40 parts.
-
Decimals: Represent parts of a whole using the base-10 system. Decimals use a point (.) to separate the whole number from the fractional part.
-
Percentages: Express parts of a whole as a fraction of 100. The percentage symbol (%) signifies "per hundred."
These three systems are interchangeable. Understanding this interoperability is key to mastering mathematical concepts.
Converting 21/40 to a Percentage: A Step-by-Step Guide
There are two primary methods for converting the fraction 21/40 into a percentage:
Method 1: Converting the Fraction to a Decimal First
This method involves a two-step process:
-
Convert the fraction to a decimal: To convert 21/40 to a decimal, we divide the numerator (21) by the denominator (40):
21 ÷ 40 = 0.525
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.525 x 100 = 52.5%
Therefore, 21/40 is equal to 52.5%.
Method 2: Direct Conversion using Proportions
This method leverages the definition of a percentage as a fraction out of 100. We set up a proportion:
21/40 = x/100
To solve for 'x' (the percentage), we cross-multiply:
40x = 2100
x = 2100 ÷ 40
x = 52.5
Therefore, 21/40 is equal to 52.5%.
Understanding the Underlying Mathematical Principles
Both methods rely on the fundamental principle of equivalent fractions. A fraction remains unchanged if both the numerator and the denominator are multiplied or divided by the same non-zero number. In Method 1, we implicitly convert the fraction to an equivalent fraction with a denominator of 100. In Method 2, we explicitly use proportions to find the equivalent fraction with a denominator of 100.
Practical Applications: Where This Conversion is Useful
The ability to convert fractions to percentages has numerous practical applications:
-
Calculating grades: If you answered 21 out of 40 questions correctly on a test, your score is 52.5%.
-
Financial calculations: Understanding percentages is essential for calculating interest rates, discounts, and profit margins. For example, if a product costs $40 and you receive a discount equivalent to 21/40 of the price, you save 52.5%.
-
Data analysis and statistics: Percentages are widely used to represent proportions in data analysis and statistics. For instance, in a survey of 40 people, if 21 responded positively, the positive response rate is 52.5%.
-
Everyday life: Percentages are used frequently in everyday situations, from calculating tips in restaurants to understanding sales discounts in stores.
Common Misconceptions and How to Avoid Them
A common mistake is forgetting to multiply the decimal by 100 when converting from a decimal to a percentage. Always remember that a percentage is a fraction out of 100. Another common error involves incorrectly setting up the proportion when using the direct conversion method. Ensure the fraction you're converting and the percentage fraction (x/100) are equivalent.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
Yes, you can convert any fraction to a percentage using the methods described above.
Q2: What if the resulting percentage is a repeating decimal?
If the division results in a repeating decimal, you can round the percentage to a certain number of decimal places (e.g., 52.5%). The level of precision required depends on the context.
Q3: Are there other ways to convert fractions to percentages?
While the methods described are the most straightforward, other techniques involve using calculators or software with built-in conversion functions.
Q4: Why is it important to understand percentage calculations?
Understanding percentage calculations is crucial for comprehending data, making informed decisions in various aspects of life, and excelling in fields like finance, statistics, and science.
Q5: How can I improve my skills in fraction to percentage conversion?
Practice is key! Work through various examples, and try converting different fractions to percentages using both methods. Familiarize yourself with the concept of equivalent fractions and the principles of proportions.
Conclusion: Mastering the Conversion of 21/40 to a Percentage and Beyond
Converting 21/40 to a percentage, which equals 52.5%, is a simple yet fundamental skill in mathematics. Understanding the underlying principles – the interconnectedness of fractions, decimals, and percentages, and the concept of equivalent fractions – is vital for efficient and accurate calculations. By mastering this conversion, you gain a powerful tool applicable in numerous contexts, from academic settings to real-world problem-solving. Remember to practice regularly, and don't hesitate to revisit the steps and explanations provided in this article to solidify your understanding. The ability to confidently navigate fraction-to-percentage conversions empowers you to approach mathematical challenges with increased efficiency and accuracy. This skill forms a strong foundation for further exploration of mathematical concepts and their diverse applications in the world around us.
Latest Posts
Latest Posts
-
1 1 2 Halved
Sep 14, 2025
-
2 Of 300 000
Sep 14, 2025
-
0 6 Divided By 4
Sep 14, 2025
-
155 Km In Mph
Sep 14, 2025
-
60 5 Kg To Pounds
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 21/40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.