25 Percent Of 20
renascent
Sep 15, 2025 · 5 min read
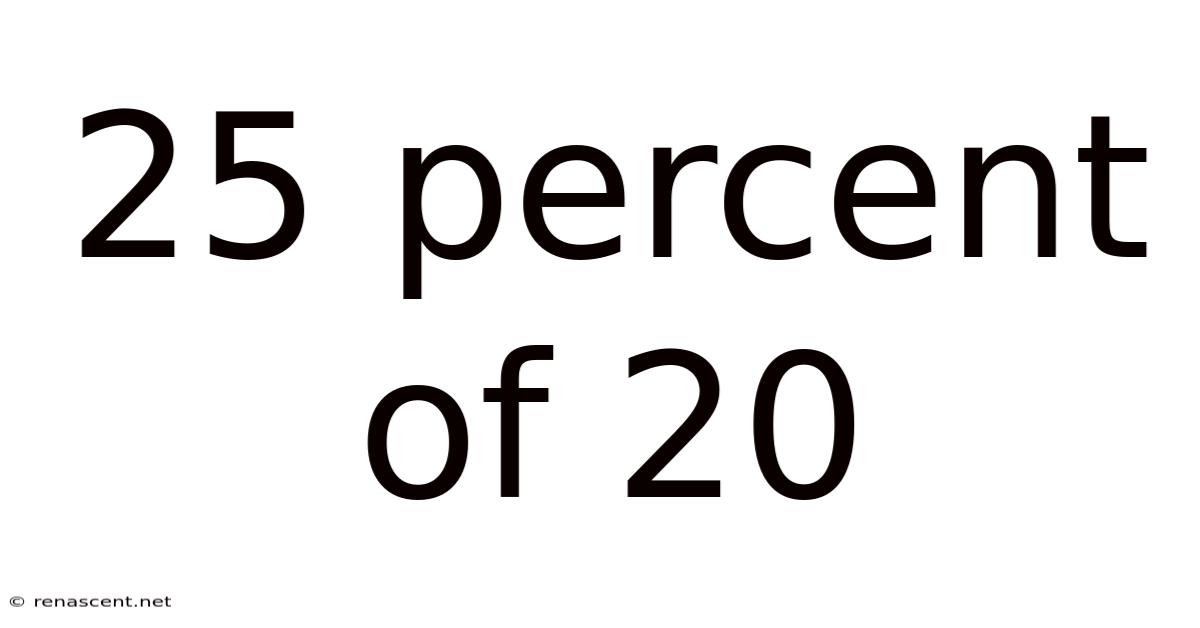
Table of Contents
Decoding 25 Percent of 20: A Comprehensive Guide to Percentages
Finding 25 percent of 20 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding the underlying principles of percentages is crucial for navigating various aspects of daily life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article will delve deep into the calculation of 25% of 20, exploring different methods, their applications, and the broader context of percentage calculations. We'll also address frequently asked questions and explore real-world scenarios where this seemingly basic calculation plays a significant role.
Understanding Percentages: The Foundation
Before we jump into calculating 25% of 20, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 25% can be written as 25/100, or its simplified fraction, 1/4. This means 25% represents 25 parts out of a total of 100 equal parts.
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method for calculating percentages. We convert the percentage to its decimal equivalent and then multiply it by the number.
Steps:
-
Convert the percentage to a decimal: To convert 25% to a decimal, divide it by 100. This gives us 25/100 = 0.25.
-
Multiply the decimal by the number: Multiply the decimal (0.25) by the number we're interested in, which is 20. So, 0.25 * 20 = 5.
Therefore, 25% of 20 is 5.
Method 2: Using Fractions
This method utilizes the fractional representation of the percentage. It offers a deeper understanding of the underlying mathematical concepts.
Steps:
-
Express the percentage as a fraction: As mentioned earlier, 25% can be expressed as the fraction 25/100, which simplifies to 1/4.
-
Multiply the fraction by the number: Multiply the fraction (1/4) by the number 20: (1/4) * 20 = 20/4 = 5.
Again, we arrive at the answer: 25% of 20 is 5.
Method 3: Proportion Method
This method utilizes the concept of proportions to solve percentage problems. It's particularly useful for more complex percentage calculations.
Steps:
-
Set up a proportion: We can set up a proportion as follows: 25/100 = x/20, where 'x' represents the unknown value (25% of 20).
-
Cross-multiply: Cross-multiply to solve for x: 25 * 20 = 100 * x. This simplifies to 500 = 100x.
-
Solve for x: Divide both sides by 100: x = 500/100 = 5.
Once more, the result is: 25% of 20 is 5.
Real-World Applications: Where Percentages Matter
The seemingly simple calculation of 25% of 20 has numerous practical applications in everyday life. Here are a few examples:
-
Discounts: Imagine a store offering a 25% discount on an item priced at $20. Using our calculation, the discount amount would be $5, and the final price would be $15 ($20 - $5).
-
Taxes: If a sales tax is 25% and the pre-tax price of an item is $20, the tax amount would be $5, bringing the total price to $25 ($20 + $5).
-
Tips: Calculating a 25% tip on a $20 meal is also straightforward. The tip amount would be $5.
-
Grade Calculations: In educational settings, percentages are frequently used to represent grades. If a student scores 25% on a 20-point quiz, they earned 5 points.
-
Financial Analysis: Percentage changes are fundamental in analyzing financial data. For instance, understanding the percentage increase or decrease in profits, sales, or investments relies heavily on these calculations.
-
Statistical Analysis: Percentages are extensively used in statistical data representation to illustrate proportions, trends, and probabilities. Understanding percentages is crucial for interpreting graphs, charts, and statistical reports accurately.
Beyond the Basics: Expanding Your Percentage Skills
While understanding how to calculate 25% of 20 is a foundational step, mastering percentages requires exploring more complex scenarios:
-
Calculating percentages of larger numbers: The same principles apply when dealing with larger numbers. For example, finding 25% of 200 involves the same steps, resulting in an answer of 50.
-
Calculating percentages of numbers with decimals: The methods remain consistent even when working with decimal numbers. For instance, finding 25% of 20.50 involves multiplying 0.25 by 20.50, which equals 5.125.
-
Finding the original number from a percentage: This involves working backward. For example, if 25% of a number is 5, we can find the original number by dividing 5 by 0.25 (or multiplying by 4), which yields 20.
-
Calculating percentage change: This involves determining the percentage increase or decrease between two values. The formula for percentage change is: [(New Value - Old Value) / Old Value] * 100.
-
Compound interest calculations: Compound interest involves earning interest on both the principal amount and accumulated interest. Mastering percentage calculations is crucial for understanding and calculating compound interest accurately.
Frequently Asked Questions (FAQ)
Q1: What are some common mistakes people make when calculating percentages?
A1: Common mistakes include:
- Incorrect decimal conversion: Mistaking 25% for 0.25 or 2.5.
- Incorrect order of operations: Forgetting the order of operations (PEMDAS/BODMAS) when dealing with more complex calculations.
- Misunderstanding percentage change calculations: Incorrectly applying the formula for percentage change.
Q2: Are there any online tools or calculators for calculating percentages?
A2: Yes, many online percentage calculators are readily available. These calculators can be helpful for double-checking calculations or for more complex percentage problems. However, understanding the underlying principles is essential for problem-solving and critical thinking.
Q3: How can I improve my understanding of percentages?
A3: Practice is key. Try working through various percentage problems of increasing difficulty. Visual aids like charts and diagrams can also help understand the concepts. Finally, seeking help from tutors or teachers can clarify any confusion.
Q4: Why are percentages important in everyday life?
A4: Percentages are used extensively in various contexts, including finance, shopping, budgeting, data analysis, and more. Understanding percentages helps you make informed decisions in various aspects of your life.
Conclusion: Mastering the Power of Percentages
While calculating 25% of 20 might seem like a basic task, it serves as a gateway to understanding the broader world of percentages. This seemingly simple calculation underpins various aspects of our daily lives, from financial planning to understanding statistical data. By mastering the different methods of calculating percentages and practicing regularly, you equip yourself with a valuable skill applicable across diverse fields. Remember, the ability to calculate percentages efficiently and accurately is a crucial life skill that will benefit you in numerous ways. So, keep practicing, keep exploring, and unlock the power of percentages!
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.