2x 3 2 Expand
renascent
Sep 17, 2025 · 5 min read
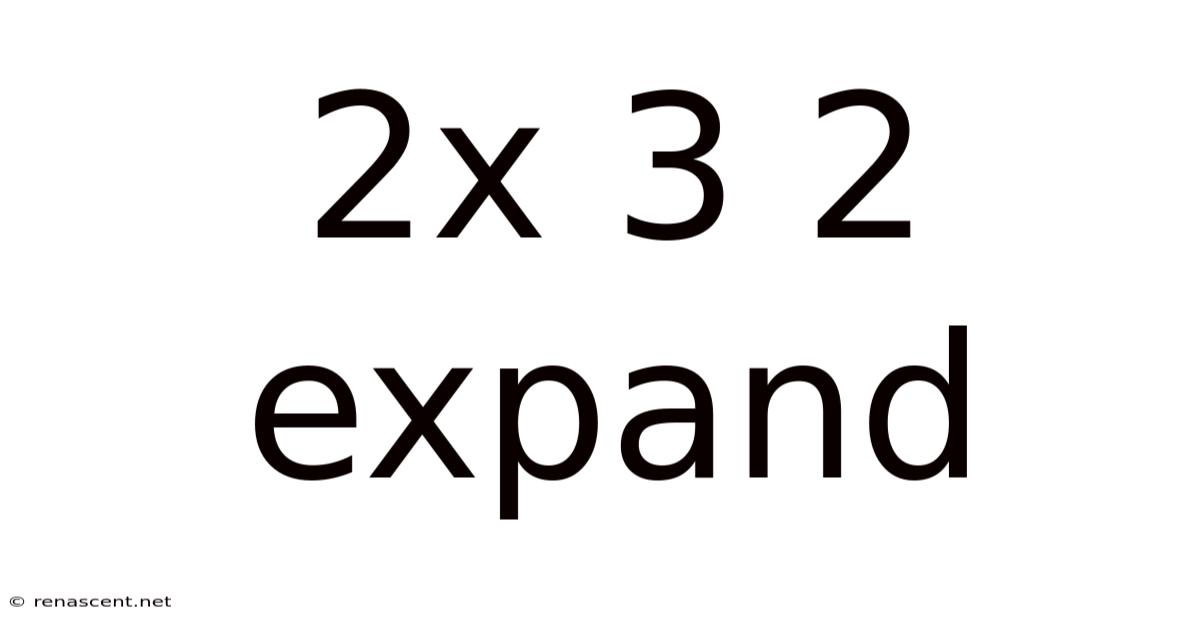
Table of Contents
Decoding the Enigma: A Deep Dive into 2x3^2 Expansion
This article explores the mathematical expression "2 x 3^2," breaking down its components, explaining its solution, and extending the concept to encompass broader mathematical principles. Understanding this seemingly simple equation opens doors to a deeper appreciation of exponents, order of operations, and the fundamental building blocks of algebra. We'll delve into the intricacies of the calculation, explore common misconceptions, and provide practical examples to solidify your understanding.
Understanding the Components
Before tackling the expansion of 2 x 3^2, let's dissect its individual components:
-
2: This is a simple integer, representing the number two. It's a coefficient in this expression, meaning it's a multiplicative factor.
-
x: This is the multiplication symbol, indicating the operation we need to perform between the coefficient (2) and the exponential term (3^2).
-
3^2: This is an exponential expression. Let's break it down further:
- 3: This is the base, the number being multiplied.
- ^2: This is the exponent or power, indicating how many times the base is multiplied by itself. In this case, it's 2, meaning 3 x 3.
The Order of Operations: PEMDAS/BODMAS
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), dictates the sequence in which mathematical operations should be performed. This is crucial to arriving at the correct answer. In 2 x 3^2, exponents take precedence over multiplication.
Expanding 2 x 3^2: Step-by-Step Solution
-
Exponents First: We begin by calculating 3^2. This means 3 multiplied by itself: 3 x 3 = 9.
-
Multiplication: Now that we've simplified the exponential term, we perform the multiplication: 2 x 9 = 18.
Therefore, the expansion of 2 x 3^2 is 18.
Beyond the Basics: Expanding the Concept
While the expansion of 2 x 3^2 is straightforward, understanding the underlying principles allows us to tackle more complex expressions. Let's explore some related concepts:
-
Different Bases and Exponents: The same principles apply to expressions with different bases and exponents. For instance, 5 x 2^3 would be solved as follows:
- Exponent: 2^3 = 2 x 2 x 2 = 8
- Multiplication: 5 x 8 = 40
-
Multiple Operations: Expressions can involve multiple operations and require careful application of PEMDAS/BODMAS. Consider: 4 + 2 x 5^2 – 10.
- Exponent: 5^2 = 25
- Multiplication: 2 x 25 = 50
- Addition and Subtraction: 4 + 50 – 10 = 44
-
Negative Exponents: Negative exponents denote reciprocals. For example, 3^-2 = 1/(3^2) = 1/9.
-
Fractional Exponents: Fractional exponents represent roots. For instance, 9^(1/2) is the square root of 9, which is 3. Similarly, 8^(1/3) is the cube root of 8, which is 2.
-
Combining Exponents: When multiplying terms with the same base, we add the exponents. For example, 3^2 x 3^3 = 3^(2+3) = 3^5 = 243. When dividing terms with the same base, we subtract the exponents. For example, 3^5 / 3^2 = 3^(5-2) = 3^3 = 27.
Common Misconceptions and Pitfalls
A frequent mistake is performing the multiplication before the exponentiation. Remember, following PEMDAS/BODMAS is essential to obtain the correct result. Incorrectly calculating 2 x 3^2 as (2 x 3)^2 = 6^2 = 36 is a common error.
Another pitfall arises when dealing with more complex expressions containing parentheses or brackets. Always perform operations within parentheses first, before applying the remaining order of operations.
Practical Applications
Understanding exponents and the order of operations is fundamental to various fields, including:
-
Science: Calculating exponential growth (like population growth or radioactive decay), determining the area or volume of objects with exponential dimensions, and many other scientific calculations.
-
Engineering: Designing structures, calculating forces, and analyzing dynamic systems often require manipulating exponential expressions.
-
Finance: Calculating compound interest, projecting investments, and assessing financial growth rely heavily on exponential functions.
-
Computer Science: Algorithms and data structures frequently utilize exponential operations. Understanding these concepts is essential for designing efficient and scalable software.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 2 x 3^2 and (2 x 3)^2?
- A: The difference lies in the order of operations. 2 x 3^2 calculates the exponent first (3^2 = 9), then performs the multiplication (2 x 9 = 18). (2 x 3)^2 calculates the expression within the parentheses first (2 x 3 = 6), then squares the result (6^2 = 36). These expressions yield different results.
-
Q: Can I use a calculator to solve this?
- A: Yes, most scientific calculators will correctly handle the order of operations. However, understanding the underlying principles is crucial, especially when tackling more complex problems.
-
Q: What happens if the exponent is 0?
- A: Any non-zero number raised to the power of 0 is equal to 1. For example, 3^0 = 1.
-
Q: What if the exponent is a negative number?
- A: A negative exponent means the reciprocal of the base raised to the positive exponent. For example, 3^-2 = 1/3^2 = 1/9.
Conclusion
Expanding 2 x 3^2 might seem trivial at first glance. However, understanding its solution reveals a fundamental understanding of exponents and the crucial role of the order of operations in mathematics. This seemingly simple expression serves as a gateway to more advanced mathematical concepts, highlighting the importance of mastering foundational principles to confidently navigate the complexities of higher-level mathematics and its applications in various fields. By grasping these concepts, you're not just solving an equation, you're building a solid foundation for future mathematical explorations. Remember the power of PEMDAS/BODMAS and the underlying principles of exponents – they are your key to unlocking a deeper understanding of the mathematical world.
Latest Posts
Latest Posts
-
Rock Cycle Flow Chart
Sep 17, 2025
-
132 Fahrenheit To Celsius
Sep 17, 2025
-
14 Ounce To Ml
Sep 17, 2025
-
156 Lb To Kg
Sep 17, 2025
-
Best Photo Printer Australia
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2x 3 2 Expand . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.