3 4 Of 105
renascent
Sep 21, 2025 · 5 min read
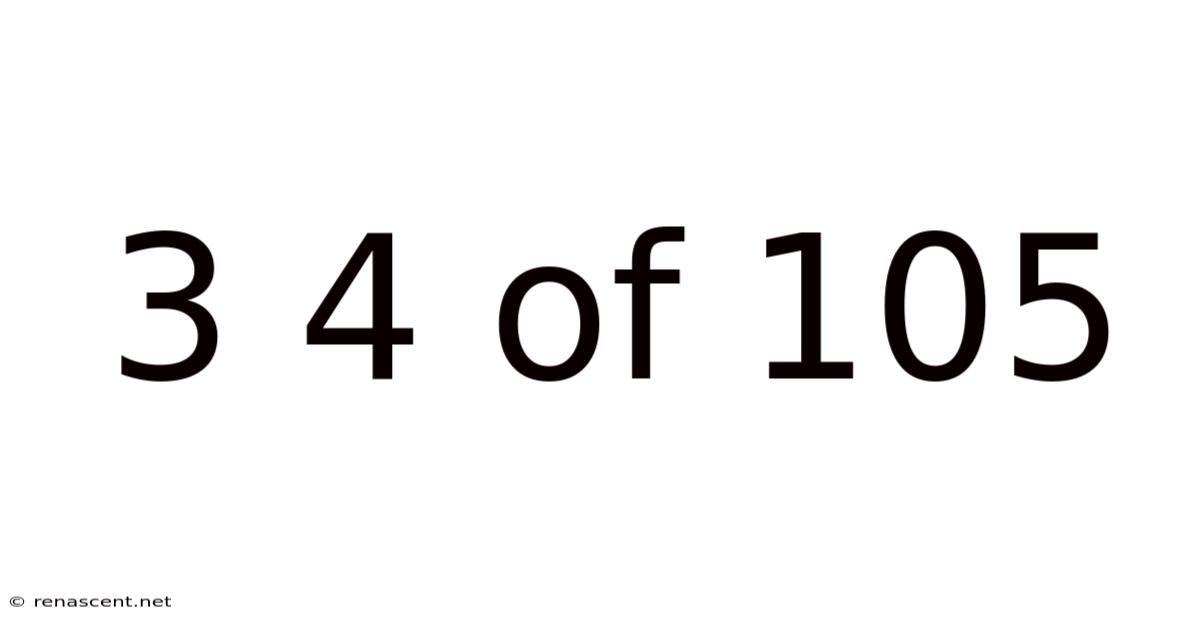
Table of Contents
Decoding 3/4 of 105: A Deep Dive into Fractions, Percentages, and Problem-Solving
Understanding fractions and percentages is a cornerstone of mathematical literacy. This seemingly simple question, "What is 3/4 of 105?", opens a door to exploring various approaches to solving similar problems and solidifying our understanding of fundamental mathematical concepts. This article will not only answer the question but will also provide a detailed explanation of the underlying principles, explore different solution methods, and delve into the practical applications of such calculations. We'll also address frequently asked questions and offer tips for tackling more complex problems involving fractions and percentages.
Understanding the Problem: 3/4 of 105
The phrase "3/4 of 105" translates directly into a mathematical expression: (3/4) * 105. This indicates we need to find three-quarters of the number 105. This seemingly simple problem allows us to explore several valuable mathematical concepts, including:
- Fractions: Understanding the concept of fractions – a part of a whole. In this case, 3/4 represents three parts out of a total of four equal parts.
- Multiplication of Fractions and Whole Numbers: The core of the problem involves multiplying a fraction by a whole number.
- Simplification and Reduction: We can simplify the calculation to make it easier to solve.
- Percentage Equivalents: We can express the fraction 3/4 as a percentage and apply that percentage to 105.
Method 1: Direct Multiplication
The most straightforward method is to directly multiply the fraction by the whole number:
(3/4) * 105 = (3 * 105) / 4
First, multiply the numerator (3) by the whole number (105):
3 * 105 = 315
Then, divide the result by the denominator (4):
315 / 4 = 78.75
Therefore, 3/4 of 105 is 78.75.
Method 2: Simplification Before Multiplication
We can simplify the calculation by reducing the fraction before performing the multiplication. Since 105 is divisible by 5, and 4 is not, we can simplify the calculation only if we express 105 as a fraction:
(3/4) * (105/1) = (3 * 105) / (4 * 1)
This leads us to the same calculation as before: 315/4 = 78.75
Method 3: Converting to Percentage
Another approach involves converting the fraction 3/4 into a percentage. To do this, we divide the numerator by the denominator and multiply by 100:
(3/4) * 100 = 75%
Now, we can find 75% of 105:
(75/100) * 105 = 0.75 * 105 = 78.75
This method demonstrates the interchangeable nature of fractions and percentages.
Method 4: Finding a Quarter, Then Multiplying by Three
We can break down the problem into smaller, more manageable steps. First, find one-quarter (1/4) of 105:
105 / 4 = 26.25
Then, multiply this result by three to find three-quarters (3/4):
26.25 * 3 = 78.75
This method is particularly useful when dealing with larger numbers or fractions that are easily divisible.
The Importance of Understanding the Underlying Concepts
The simplicity of the problem "3/4 of 105" belies the richness of the mathematical concepts involved. Mastering these concepts is crucial for:
- Everyday Calculations: From calculating discounts to determining portions of recipes, understanding fractions and percentages is essential in daily life.
- Advanced Mathematics: Fractions form the foundation for more complex mathematical concepts like algebra, calculus, and statistics.
- Problem-Solving Skills: Solving this problem, using different methods, enhances our problem-solving abilities and allows us to approach similar challenges from various perspectives.
Practical Applications: Real-world Scenarios
The principles demonstrated in solving "3/4 of 105" have widespread applications:
- Financial Calculations: Calculating interest, discounts, tax, and profit margins all involve working with fractions and percentages. For instance, if a store offers a 25% discount on an item costing $105, the discount amount is calculated as (25/100) * 105 = $26.25.
- Measurement and Conversion: Converting units of measurement often involves using fractions and percentages. Imagine calculating the area of a room that is 3/4 of a meter wide and 2 meters long.
- Data Analysis: In statistics and data analysis, understanding percentages helps to interpret data and draw conclusions.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Absolutely! Calculators are powerful tools for performing these calculations quickly and accurately. However, it's beneficial to understand the underlying mathematical principles before relying solely on a calculator.
Q: What if the fraction was more complex, like 17/25 of 105?
A: The same principles apply. You would multiply the numerator (17) by 105 and then divide by the denominator (25). You could also convert 17/25 into a decimal or percentage first.
Q: Why are there multiple methods to solve this problem?
A: Different methods cater to varying preferences and levels of understanding. Some methods are more efficient than others depending on the specific numbers involved. Understanding multiple methods deepens your mathematical understanding and flexibility.
Q: Are there any online tools or resources to help with fraction and percentage calculations?
A: While I cannot provide links to external websites, many free online resources, calculators, and educational websites offer assistance with fraction and percentage problems.
Conclusion: Mastering Fractions and Percentages
This seemingly simple problem of finding 3/4 of 105 provides a valuable opportunity to explore and reinforce the fundamental concepts of fractions and percentages. Mastering these concepts is crucial for navigating everyday situations and building a strong foundation for more advanced mathematical concepts. By employing different solution methods and understanding the underlying principles, you'll not only answer the question but also gain a deeper appreciation for the power and versatility of mathematical problem-solving. Remember, practice makes perfect! The more you work with fractions and percentages, the more comfortable and confident you'll become. So, keep practicing, keep exploring, and keep building your mathematical skills!
Latest Posts
Latest Posts
-
Quotes About John Proctor
Sep 21, 2025
-
4 Of 100 000
Sep 21, 2025
-
4 X 5 3
Sep 21, 2025
-
19 24 X 100
Sep 21, 2025
-
Open Source Software Drawbacks
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Of 105 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.