3 4 X 45
renascent
Sep 22, 2025 · 5 min read
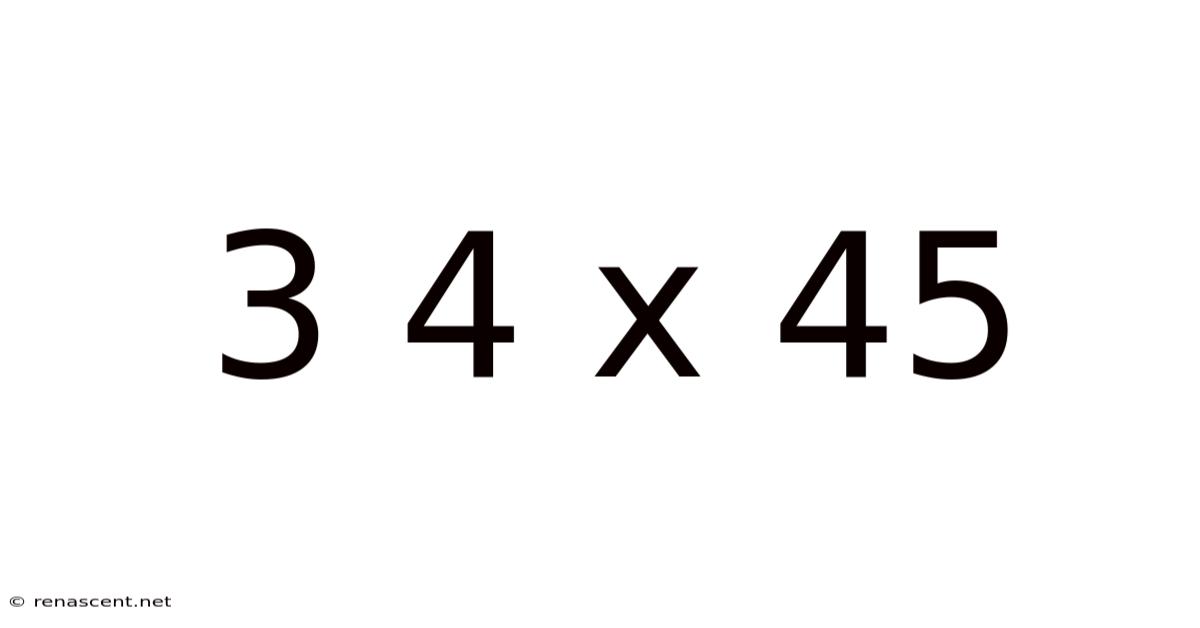
Table of Contents
Decoding 3 x 4 x 45: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "3 x 4 x 45," delving far beyond the basic calculation to uncover the underlying principles of multiplication, its practical applications in various fields, and its role in developing crucial problem-solving skills. We will examine different approaches to solving this problem, explore related mathematical concepts, and consider the broader implications of understanding multiplicative relationships. Understanding 3 x 4 x 45 is not just about finding the answer; it's about understanding the why behind the calculation and its relevance in the real world.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is a simplified form of repeated addition. The expression "3 x 4 x 45" can be interpreted as:
-
3 groups of (4 groups of 45): This highlights the hierarchical nature of multiplication, where we are dealing with nested sets. We first calculate 4 groups of 45, and then we take 3 groups of that result.
-
Repeated addition: We could express this as 45 + 45 + 45 + 45 (four times), and then add that result to itself three times. While tedious, this approach demonstrates the fundamental connection between addition and multiplication.
This fundamental understanding forms the bedrock for more complex mathematical operations and problem-solving.
Calculating 3 x 4 x 45: Step-by-Step Approaches
There are several ways to approach this calculation, each illustrating different aspects of mathematical flexibility:
Method 1: Sequential Multiplication
This is the most straightforward approach:
- Multiply 3 and 4: 3 x 4 = 12
- Multiply the result by 45: 12 x 45 = 540
Therefore, 3 x 4 x 45 = 540
Method 2: Commutative Property
The commutative property of multiplication states that the order of numbers does not affect the result. We can rearrange the numbers for easier calculation:
- Multiply 3 and 45: 3 x 45 = 135
- Multiply the result by 4: 135 x 4 = 540
This method leverages the commutative property to simplify the calculation by multiplying smaller numbers first.
Method 3: Distributive Property
The distributive property allows us to break down multiplication into smaller, more manageable parts:
- Rewrite 45 as 40 + 5: This allows us to use the distributive property to simplify the calculation.
- Apply the distributive property: (3 x 4) x (40 + 5) = (12 x 40) + (12 x 5) = 480 + 60 = 540
This method demonstrates the power of breaking down complex problems into simpler components.
Beyond the Calculation: Exploring Related Concepts
Solving 3 x 4 x 45 opens doors to exploring several crucial mathematical concepts:
-
Factors and Multiples: The numbers 3, 4, and 45 are factors of 540. Conversely, 540 is a multiple of 3, 4, and 45. Understanding factors and multiples is essential for simplifying fractions, finding common denominators, and solving algebraic equations.
-
Prime Factorization: Breaking down a number into its prime factors (numbers divisible only by 1 and themselves) provides a deeper understanding of its multiplicative structure. The prime factorization of 540 is 2² x 3³ x 5. This representation reveals the building blocks of the number, offering insights into its divisibility and relationships with other numbers.
-
Order of Operations (PEMDAS/BODMAS): While this example doesn't involve other operations, understanding the order of operations is critical for solving more complex expressions involving parentheses, exponents, multiplication, division, addition, and subtraction. The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) dictates the sequence of operations.
-
Algebraic Expressions: The concept of variables can be introduced. Imagine the expression "x * y * z," where x=3, y=4, and z=45. This transition from numerical calculation to algebraic representation prepares the foundation for more advanced mathematical concepts.
Real-World Applications: Where Multiplication Matters
The seemingly simple calculation of 3 x 4 x 45 has significant real-world applications across diverse fields:
-
Business and Finance: Calculating total costs, profits, or inventory values frequently involves multiplication. Imagine calculating the total cost of 3 boxes, each containing 4 packages of 45 items.
-
Engineering and Construction: Calculating areas, volumes, and material quantities in construction projects involves multiplication extensively. Determining the amount of concrete needed for a foundation, for instance, would necessitate multiplication.
-
Science and Research: Data analysis, statistical calculations, and scientific modeling often rely on multiplication. Calculating concentrations, dilutions, or experimental results frequently involves multiplicative relationships.
-
Everyday Life: From calculating the total cost of groceries to determining the number of tiles needed for a floor, multiplication permeates our daily lives.
Frequently Asked Questions (FAQ)
Q: What if I made a mistake in the calculation?
A: Double-check your work. Use a calculator or try a different method to verify your answer. Understanding the underlying principles allows you to identify and correct errors more effectively.
Q: Are there other ways to solve this problem?
A: Yes, there are many. You could use mental math techniques, a calculator, or even a spreadsheet program. Exploring various methods enhances your mathematical understanding and flexibility.
Q: Why is understanding multiplication so important?
A: Multiplication is a fundamental building block of mathematics. It underpins more advanced concepts, and its applications are vast and crucial in various fields. It's a crucial life skill.
Q: How can I improve my multiplication skills?
A: Practice regularly! Use flashcards, play multiplication games, and work through various problem sets. Understanding the underlying concepts, rather than rote memorization, is key to mastering multiplication.
Conclusion: Mastering Multiplication, Mastering Problem-Solving
The seemingly straightforward calculation "3 x 4 x 45" serves as a gateway to a deeper understanding of multiplication, its underlying principles, and its wide-ranging applications. Beyond simply obtaining the answer (540), this exercise emphasizes the importance of:
-
Understanding the fundamentals: Recognizing multiplication as repeated addition provides a solid foundation.
-
Exploring various approaches: Utilizing different methods enhances flexibility and problem-solving skills.
-
Connecting concepts: Relating multiplication to factors, multiples, prime factorization, and order of operations strengthens mathematical understanding.
-
Recognizing real-world applications: Understanding the practical relevance of multiplication in diverse fields underscores its importance.
Mastering multiplication is not just about memorizing multiplication tables; it's about developing a deeper conceptual understanding and applying it effectively to solve various problems. This journey of understanding 3 x 4 x 45 is a testament to the power of basic mathematics and its crucial role in navigating the complexities of the world around us.
Latest Posts
Latest Posts
-
Barium Hydroxide Ammonium Thiocyanate
Sep 22, 2025
-
8000 Hours To Days
Sep 22, 2025
-
24 Divided By 3
Sep 22, 2025
-
Latitude Of Darwin Australia
Sep 22, 2025
-
Example Of A Wedge
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3 4 X 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.