3 Divided By 29
renascent
Sep 16, 2025 · 6 min read
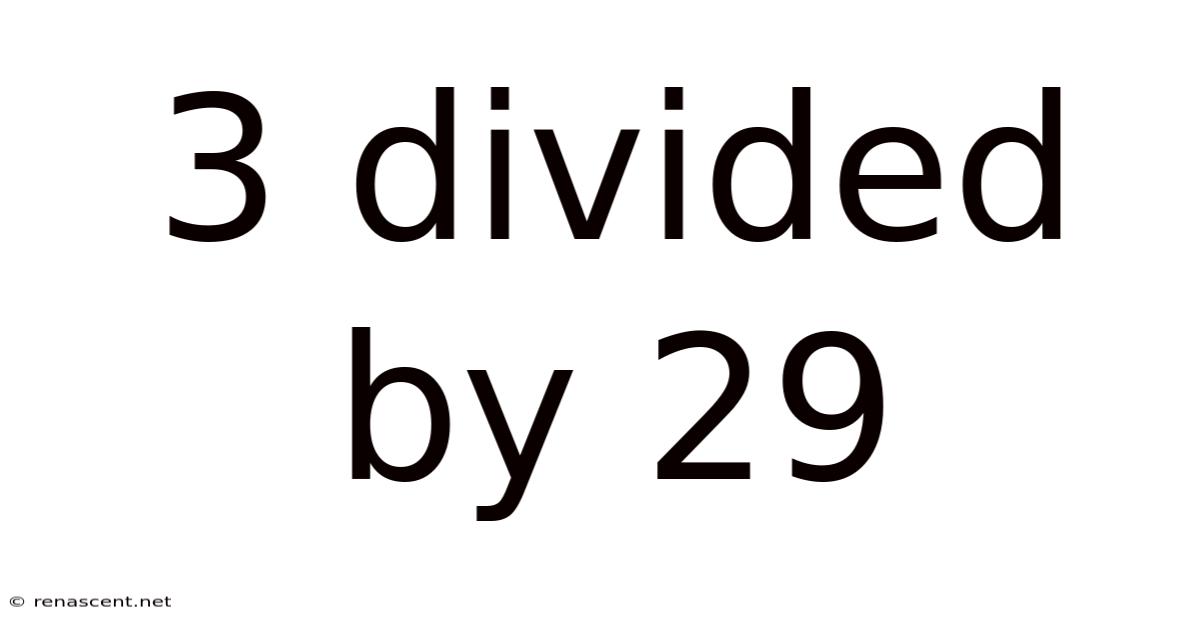
Table of Contents
Unveiling the Mystery: A Deep Dive into 3 Divided by 29
The seemingly simple question, "What is 3 divided by 29?", opens a door to a fascinating exploration of division, decimals, fractions, and even the nature of infinite numbers. While a quick calculation might provide a numerical answer, a deeper understanding reveals the rich mathematical concepts underlying this seemingly straightforward problem. This article will guide you through the process of solving 3 divided by 29, explaining the various methods and exploring the broader mathematical implications.
Introduction: Understanding Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the case of 3 divided by 29 (written as 3 ÷ 29 or 3/29), we are asking: "How many times does 29 fit into 3?" Since 29 is larger than 3, the answer will be a number less than 1, specifically a fraction or decimal.
Method 1: Long Division
The traditional method for solving this is long division. While seemingly tedious, it provides a clear step-by-step approach to understanding the process.
-
Set up the problem: Write 3 as the dividend and 29 as the divisor. You'll notice immediately that 29 doesn't go into 3 at all.
-
Add a decimal point and zeros: To continue the division, add a decimal point to the dividend (3) and add zeros as needed. This allows you to continue the division process. Now you have 3.0000...
-
Perform the long division: Begin the division process as you would with whole numbers. 29 does not go into 3, so you move to 30. 29 goes into 30 once (29 x 1 = 29). Subtract 29 from 30, leaving 1. Bring down the next zero to get 10.
-
Continue the process: 29 does not go into 10, so you bring down another zero to make 100. 29 goes into 100 three times (29 x 3 = 87). Subtract 87 from 100, leaving 13.
-
Repeat until desired accuracy: This process can be repeated indefinitely, as the division will result in a non-terminating decimal. Each step refines the accuracy of the answer. You will continue to get remainders, resulting in an infinite decimal expansion.
Therefore, 3 divided by 29 using long division provides an approximation, dependent on the number of decimal places you carry out the calculation. For example, carrying it out to four decimal places would yield approximately 0.1034.
Method 2: Using a Calculator
The easiest way to solve 3 divided by 29 is with a calculator. Simply input "3 ÷ 29" and the calculator will provide a decimal approximation. The result will be a non-terminating, repeating decimal. The accuracy of the result depends on the calculator's capabilities. Most calculators will display the result to a limited number of decimal places.
Method 3: Expressing the Result as a Fraction
The most precise way to represent the result is as a fraction: 3/29. This fraction is already in its simplest form, as 3 and 29 share no common factors other than 1. This fraction represents the exact value, unlike any decimal approximation, which is inherently an approximation.
Understanding the Decimal Representation: Non-Terminating, Repeating Decimals
The result of 3 ÷ 29 is a non-terminating, repeating decimal. This means the decimal representation goes on forever without ending and eventually repeats a sequence of digits. This is a characteristic of many fractions where the denominator (in this case, 29) has prime factors other than 2 and 5. The repeating sequence can be quite long; finding the exact repeating pattern can be a mathematical challenge, often involving techniques from number theory.
The Mathematical Significance: Rational Numbers and Infinite Series
The fraction 3/29 represents a rational number. Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero. This contrasts with irrational numbers, such as π (pi) or √2 (the square root of 2), which cannot be expressed as such a fraction and have infinite, non-repeating decimal expansions. Understanding this distinction is crucial in higher-level mathematics.
The decimal expansion of 3/29 can also be understood as an infinite series:
0.10344827586...
This series never ends but approaches the exact value of 3/29. The study of infinite series is a major branch of mathematics with applications in calculus, analysis, and numerous other fields.
Practical Applications: Beyond the Classroom
While this might seem like a purely academic exercise, the concept of dividing numbers, including instances resulting in decimal or fractional answers, has wide-ranging applications in various fields:
-
Engineering and Physics: Precise calculations are essential, and understanding decimal approximations and their limitations is crucial for accurate results.
-
Finance: Calculating interest, proportions, and shares often involves division and results in decimal values.
-
Computer Science: Understanding decimal representation is fundamental for representing numbers in computer systems and for programming calculations involving floating-point numbers.
-
Data Analysis: Dividing data sets into proportions and calculating averages often results in decimal values.
Frequently Asked Questions (FAQ)
-
Q: Is there a shortcut to calculate 3/29? A: No easy shortcut exists beyond using a calculator or approximating the result.
-
Q: Why does the decimal expansion repeat? A: The repeating nature of the decimal is due to the properties of the fraction and the prime factorization of the denominator (29).
-
Q: How many decimal places are needed for an accurate answer? A: It depends on the application. For most practical purposes, a few decimal places offer sufficient accuracy. However, for scientific or engineering purposes, a higher level of precision might be necessary.
-
Q: Can I use a different method to find the decimal representation? A: While long division is a fundamental method, you can use iterative methods or computer programs to calculate the decimal representation to a higher degree of accuracy.
Conclusion: More Than Just a Calculation
The seemingly simple problem of 3 divided by 29 offers a rich and rewarding exploration into the world of mathematics. It unveils the beauty of fractions, the intricacies of decimal representation, and the underlying principles of rational numbers and infinite series. While a calculator provides a quick numerical answer, the process of understanding the underlying mathematical concepts is far more valuable, opening doors to deeper comprehension and appreciation of the mathematical world around us. From simple calculations to complex scientific models, the principles demonstrated by this single division problem form the bedrock of numerous applications across diverse fields. The journey from a simple question to a profound understanding of mathematical principles is what makes this a truly enriching exercise.
Latest Posts
Latest Posts
-
200 Km Into Miles
Sep 17, 2025
-
4 25 Square Root
Sep 17, 2025
-
Funeral Oration By Pericles
Sep 17, 2025
-
Area Of A Park
Sep 17, 2025
-
110 Km In Miles
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 Divided By 29 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.