30 Percent Of 45
renascent
Sep 16, 2025 · 5 min read
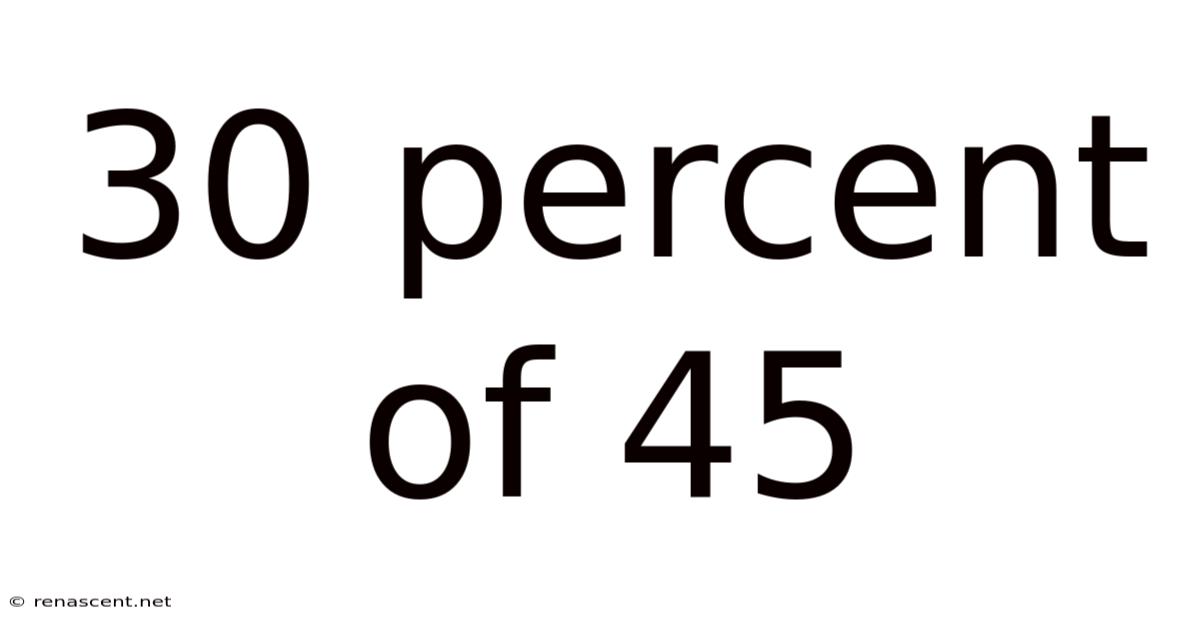
Table of Contents
Unveiling the Mystery: Calculating 30% of 45 and Beyond
Finding 30% of 45 might seem like a simple calculation, a quick task for a calculator. However, understanding the underlying principles of percentages and exploring different methods of calculation opens up a world of mathematical understanding that extends far beyond this seemingly basic problem. This article will delve into various ways to solve this problem, explaining the concepts involved, and providing a deeper understanding of percentages and their applications in everyday life. This will equip you not only to calculate 30% of 45 but also to tackle any percentage calculation with confidence.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 30% means 30 out of 100, or 30/100, which can be simplified to 3/10. This understanding forms the bedrock of all percentage calculations. When we ask "What is 30% of 45?", we are essentially asking "What is 30/100 * 45?".
Method 1: The Direct Calculation
This is the most straightforward method. We directly translate the problem into a mathematical equation:
30% of 45 = (30/100) * 45
This simplifies to:
0.3 * 45 = 13.5
Therefore, 30% of 45 is 13.5.
Method 2: Breaking it Down
Sometimes, breaking down a percentage calculation into smaller, more manageable parts can be helpful, especially for mental calculations. We can express 30% as 10% + 10% + 10%. Let's find 10% of 45 first:
10% of 45 = (10/100) * 45 = 4.5
Since 30% is three times 10%, we simply multiply this result by 3:
3 * 4.5 = 13.5
This confirms our previous result: 30% of 45 is 13.5.
Method 3: Using Decimal Equivalents
This method leverages the fact that percentages can easily be converted into decimal numbers. We know that 30% is equivalent to 0.30 (or simply 0.3). Therefore, the calculation becomes:
0.3 * 45 = 13.5
This is a quick and efficient method, especially when using a calculator.
Method 4: Proportion Method
This method utilizes the concept of proportions. We set up a proportion where we relate the part (x) to the whole (45) and the percentage (30) to 100:
x/45 = 30/100
To solve for x, we cross-multiply:
100x = 30 * 45
100x = 1350
x = 1350 / 100
x = 13.5
This method highlights the relationship between the percentage and the actual value, reinforcing the concept of proportions.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations isn't just about solving math problems; it's a crucial skill with widespread real-world applications. Here are a few examples:
-
Sales and Discounts: Retail stores frequently offer discounts expressed as percentages. If a shirt costs $45 and is on sale for 30% off, you would calculate 30% of $45 to determine the discount amount ($13.50), then subtract that from the original price to find the sale price ($31.50).
-
Taxes: Sales taxes are usually expressed as a percentage of the purchase price. Calculating the tax amount requires finding a percentage of the total cost.
-
Tips and Gratuities: When dining out, calculating a tip is a percentage calculation. A 20% tip on a $45 bill is a common practice.
-
Financial Calculations: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding percentage calculations is essential for managing personal finances effectively.
-
Statistics and Data Analysis: Percentages are widely used to represent data in reports, charts, and graphs, making it easier to visualize and interpret information. For example, a survey might reveal that 30% of respondents prefer a certain product.
-
Grade Calculations: In education, grades are often expressed as percentages. Understanding percentage calculations helps students determine their overall scores and academic standing.
Expanding the Understanding: Beyond 30% of 45
While we've focused on finding 30% of 45, the principles we've discussed apply to any percentage calculation. Let's consider a few variations:
-
Finding other percentages of 45: To find any percentage (say, 15%) of 45, we would simply substitute that percentage (15/100 or 0.15) into our equation.
-
Finding a percentage of different numbers: The same methods can be applied to find a percentage of any number. For instance, finding 30% of 70 would involve calculating (30/100) * 70 = 21.
-
Working backward: We can also use percentage calculations to find the original value if we know a percentage and its corresponding amount. For instance, if 30% of a number is 13.5, we can find the original number by dividing 13.5 by 0.3, which gives us 45.
Frequently Asked Questions (FAQs)
Q: What is the easiest method to calculate percentages?
A: The easiest method depends on your preference and the tools available. Using decimal equivalents (Method 3) is generally quick and efficient, particularly with a calculator. The breakdown method (Method 2) can be helpful for mental calculations.
Q: Why is understanding percentages important?
A: Understanding percentages is crucial for everyday life, from managing personal finances to interpreting data and making informed decisions in various contexts.
Q: Are there any online tools or calculators available to help with percentage calculations?
A: Yes, many online calculators and tools are available to assist with percentage calculations. However, understanding the underlying principles is essential to avoid reliance on technology alone and to grasp the concepts fully.
Q: Can I use a different fraction to represent 30%?
A: Yes, absolutely. 30% is equivalent to 30/100, which can be simplified to 3/10, 6/20, 15/50, and many other equivalent fractions. The choice of fraction will not affect the final result.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 30% of 45, while seemingly simple, provides a gateway to a deeper understanding of percentages and their widespread applications. By mastering different calculation methods, you'll equip yourself with a valuable skill that extends far beyond solving simple math problems. From navigating everyday finances to interpreting data, the ability to understand and apply percentages is a valuable asset that will contribute to your success in many areas of life. Remember, the journey of learning is continuous; embracing the challenges and exploring different approaches will lead to a more profound and practical understanding of mathematics and its relevance in the world around us.
Latest Posts
Latest Posts
-
125 Kilograms To Pounds
Sep 16, 2025
-
Rear Vision Mirror Accessories
Sep 16, 2025
-
450 Yards To Meters
Sep 16, 2025
-
160 Min In Hours
Sep 16, 2025
-
Christmas Present With Tag
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 30 Percent Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.