34/50 As A Percentage
renascent
Sep 17, 2025 · 5 min read
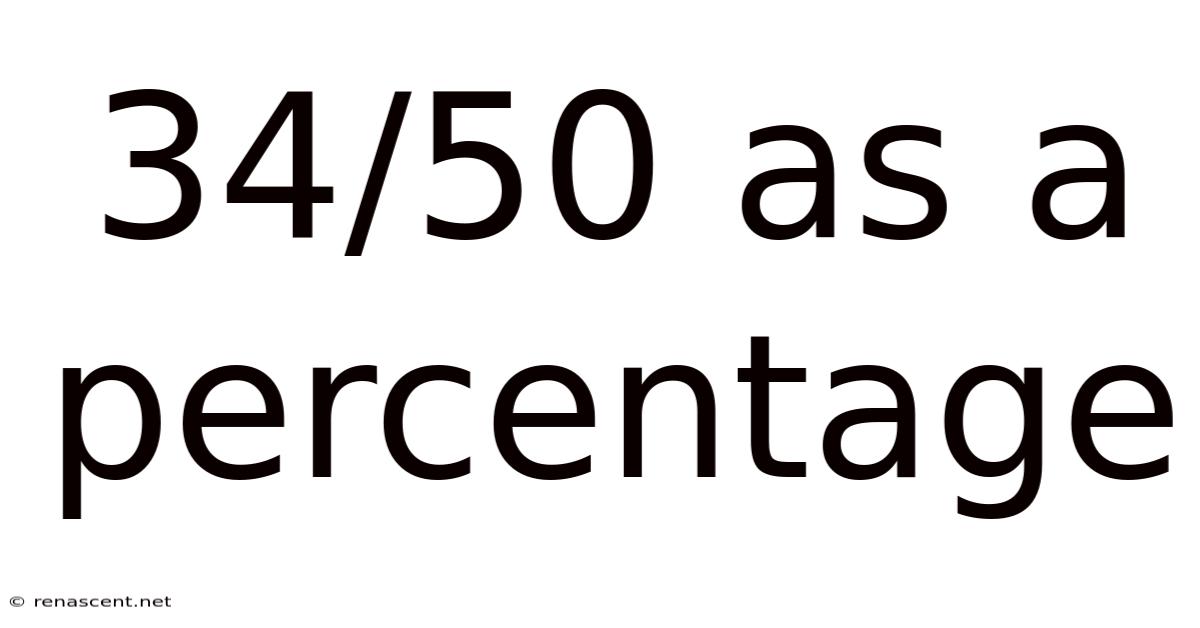
Table of Contents
34/50 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific calculations. This article provides a comprehensive guide on how to convert the fraction 34/50 into a percentage, explaining the process step-by-step and delving into the underlying mathematical concepts. We will also explore various practical applications and address frequently asked questions to solidify your understanding. This guide is perfect for students, professionals, or anyone looking to improve their numerical literacy.
Introduction: Understanding Fractions and Percentages
Before diving into the conversion of 34/50, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 34/50, 34 is the numerator, and 50 is the denominator. This means 34 out of 50 parts of a whole.
A percentage, on the other hand, is a way of expressing a fraction or a proportion as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Converting fractions to percentages involves finding the equivalent fraction with a denominator of 100. This allows us to express the fraction as a number followed by the "%" symbol.
Method 1: Direct Conversion using Decimal
The most straightforward method to convert 34/50 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (34) by the denominator (50).
34 ÷ 50 = 0.68
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
0.68 × 100 = 68%
Therefore, 34/50 is equal to 68%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method demonstrates the core concept of percentages – expressing a proportion as a value out of 100.
-
Find a common factor: Determine a number that can divide both the numerator and the denominator evenly. In this case, both 34 and 50 are divisible by 2.
-
Simplify the fraction: Divide both the numerator and the denominator by the common factor (2).
34 ÷ 2 = 17 50 ÷ 2 = 25
This simplifies the fraction to 17/25.
-
Convert to an equivalent fraction with a denominator of 100: To achieve a denominator of 100, we need to multiply both the numerator and denominator by a number that results in 100 in the denominator. Since 25 × 4 = 100, we multiply both parts of the fraction by 4:
17 × 4 = 68 25 × 4 = 100
This gives us the equivalent fraction 68/100.
-
Express as a percentage: Since a percentage is a fraction out of 100, 68/100 is directly equivalent to 68%.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage. We set up a proportion where x represents the percentage we want to find:
34/50 = x/100
To solve for x, we cross-multiply:
50x = 3400
Then, divide both sides by 50:
x = 3400 ÷ 50 = 68
Therefore, x = 68, meaning 34/50 is equal to 68%.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates. For example, if you receive a 68% discount on a product, it means you pay only 32% of the original price.
-
Statistics: Analyzing data, expressing probabilities, and interpreting survey results. If 34 out of 50 people surveyed prefer a particular brand, this represents a 68% preference rate.
-
Science: Expressing experimental results, calculating concentrations, and representing data in charts and graphs. A 68% yield in a chemical reaction indicates that 68% of the expected product was obtained.
-
Everyday Life: Calculating tips, understanding sales, and comparing prices. Knowing that 34/50 is 68% can help you quickly assess discounts or proportions in everyday situations.
Understanding the Significance of 68%
The result of 68% isn't just a numerical value; it represents a significant proportion. It's well above the halfway point (50%) indicating a substantial portion of the whole. In statistical contexts, 68% often holds particular meaning. For instance, in a normal distribution, approximately 68% of the data falls within one standard deviation of the mean. This percentage frequently appears in statistical analyses and interpretations.
Frequently Asked Questions (FAQs)
Q1: Can I convert any fraction to a percentage?
A1: Yes, any fraction can be converted to a percentage by dividing the numerator by the denominator and multiplying the result by 100.
Q2: What if the decimal resulting from the fraction division is long and non-terminating?
A2: In such cases, you can round the decimal to a desired number of decimal places before multiplying by 100. For instance, if you get a decimal like 0.68333..., you can round it to 0.68 or 0.683, depending on the required precision.
Q3: Are there any online tools or calculators to convert fractions to percentages?
A3: Yes, many online calculators are available that can perform this conversion instantly. However, understanding the underlying method is crucial for applying the concept effectively.
Q4: How can I convert a percentage back to a fraction?
A4: To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, to convert 68% back to a fraction, divide 68 by 100, resulting in 68/100, which simplifies to 17/25.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with widespread applications. This article explored three different methods for converting 34/50 to a percentage, emphasizing the underlying concepts and providing practical examples. By understanding these methods, you can confidently tackle similar conversions and apply this knowledge to various aspects of your life, from personal finance to scientific analysis. Remember that practice is key to mastering percentage conversions, so try applying these methods to different fractions and percentages to build your confidence and understanding.
Latest Posts
Latest Posts
-
1 4 Divided By 2
Sep 17, 2025
-
Elements In Ammonium Chloride
Sep 17, 2025
-
Chart Centigrade To Fahrenheit
Sep 17, 2025
-
75 Ml To Oz
Sep 17, 2025
-
Brake Rotor Measuring Tool
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 34/50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.