36 Divided By 3
renascent
Sep 17, 2025 · 6 min read
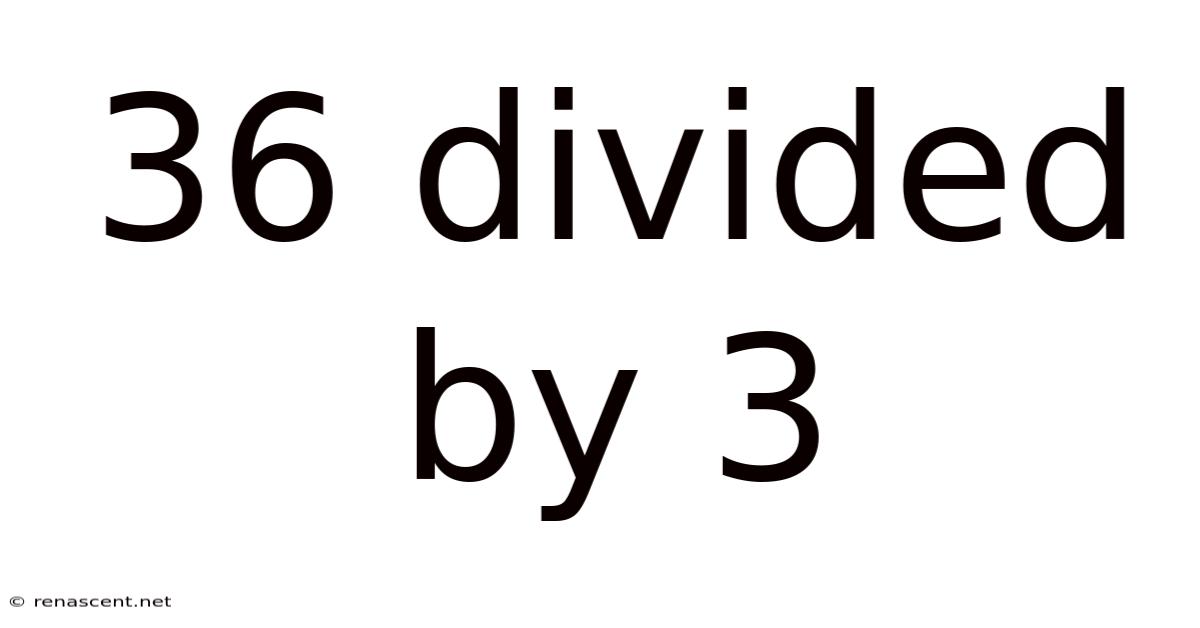
Table of Contents
36 Divided by 3: A Deep Dive into Division and Its Applications
Understanding division is a fundamental building block in mathematics, crucial for various applications from everyday life to complex scientific calculations. This article will explore the seemingly simple problem of 36 divided by 3, delving deep into the process, its underlying principles, and its significance in a broader mathematical context. We'll cover different methods of solving this problem, explore its real-world applications, and address frequently asked questions to solidify your understanding.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the problem 36 divided by 3 (often written as 36 ÷ 3, 36/3, or $\frac{36}{3}$), we are asking: "How many times does 3 fit into 36?" The answer, as we'll soon demonstrate through various methods, is 12. This simple calculation is the foundation for numerous more complex mathematical concepts and practical applications.
Methods for Solving 36 Divided by 3
There are several ways to solve 36 divided by 3, each offering a different perspective on the underlying concept of division.
-
Repeated Subtraction: This method involves subtracting the divisor (3) repeatedly from the dividend (36) until you reach zero. The number of times you subtract represents the quotient.
36 - 3 = 33 33 - 3 = 30 30 - 3 = 27 27 - 3 = 24 24 - 3 = 21 21 - 3 = 18 18 - 3 = 15 15 - 3 = 12 12 - 3 = 9 9 - 3 = 6 6 - 3 = 3 3 - 3 = 0
We subtracted 3 twelve times, therefore, 36 ÷ 3 = 12. This method is excellent for visualizing the division process, especially for beginners.
-
Long Division: Long division is a more formal algorithm used for larger numbers. While seemingly complex for this simple problem, understanding it is crucial for tackling more challenging divisions.
12 3 | 36 -3 -- 6 -6 -- 0- We begin by dividing 3 into 3 (the first digit of 36). 3 goes into 3 once (1). We write the 1 above the 3.
- Next, we multiply the quotient (1) by the divisor (3): 1 * 3 = 3. We write this below the 3.
- We subtract 3 from 3: 3 - 3 = 0.
- We bring down the next digit (6).
- We divide 3 into 6. 3 goes into 6 twice (2). We write the 2 above the 6.
- We multiply the quotient (2) by the divisor (3): 2 * 3 = 6. We write this below the 6.
- We subtract 6 from 6: 6 - 6 = 0. We have no remainder. Therefore, the answer is 12.
-
Multiplication: Division and multiplication are inverse operations. To solve 36 ÷ 3, we can ask: "What number multiplied by 3 equals 36?" The answer is 12 (because 12 x 3 = 36). This method is particularly helpful for mental arithmetic and understanding the relationship between division and multiplication.
-
Using a Number Line: A number line can visually represent the division process. Starting at 36, we repeatedly jump back by 3 until we reach 0. The number of jumps represents the quotient.
Real-World Applications of Division
The seemingly simple calculation of 36 divided by 3 has numerous practical applications in daily life:
-
Sharing Equally: Imagine you have 36 cookies to share equally among 3 friends. Dividing 36 by 3 tells you each friend gets 12 cookies.
-
Pricing and Budgeting: If 3 kilograms of apples cost $36, dividing 36 by 3 gives you the price per kilogram ($12).
-
Measurements and Conversions: Dividing quantities is essential for unit conversions. For example, if a journey is 36 kilometers and you travel at an average speed of 3 kilometers per hour, dividing 36 by 3 tells you the journey will take 12 hours.
-
Recipe Scaling: If a recipe calls for 3 cups of flour and you want to triple the recipe, multiplying the flour amount by 3 (3 x 3 = 9 cups) is the equivalent of dividing the original amount of flour in the tripled recipe by 3 to get the original amount.
-
Data Analysis: Division is fundamental in statistical analysis. Calculating averages, rates, and proportions frequently involves division.
Understanding Remainders: An Expansion of Division
While 36 divided by 3 results in a whole number (12), not all division problems yield such clean results. Some divisions leave a remainder – a portion of the dividend that cannot be evenly divided by the divisor.
Let's consider an example: 37 divided by 3.
Using long division:
12 R 1
3 | 37
-3
--
7
-6
--
1
Here, the quotient is 12, and the remainder is 1. This means 3 goes into 37 twelve times with one left over. Remainders are important in many contexts, highlighting situations where equal sharing isn't perfectly achievable.
The Significance of 36 and 3 in Number Theory
The numbers 36 and 3 have interesting properties within number theory:
-
36: 36 is a highly composite number (it has more divisors than any smaller positive integer). It's also a perfect square (6 x 6 = 36), and the sum of the first four even numbers (2 + 4 + 6 + 8 + 10 + 12 = 36).
-
3: 3 is a prime number, meaning it's only divisible by 1 and itself. Prime numbers are fundamental building blocks in number theory.
The relationship between 36 and 3 highlights the interplay between composite and prime numbers in division.
Frequently Asked Questions (FAQ)
-
What is the inverse operation of division? Multiplication is the inverse operation of division.
-
What if I divide by zero? Dividing by zero is undefined in mathematics. It's not possible to divide a number into zero equal parts.
-
How can I improve my division skills? Practice regularly with different types of division problems, starting with simpler problems and gradually increasing the difficulty. Use different methods to reinforce your understanding.
-
Are there calculators or online tools that can help with division? Yes, many calculators and online tools can perform division calculations, but understanding the underlying principles is crucial for effective problem-solving.
Conclusion: The Power of Division
The seemingly simple problem of 36 divided by 3 serves as a gateway to understanding the broader concept of division, its numerous applications, and its significance in mathematics. By exploring different methods of solving this problem, we have highlighted the connection between division and other arithmetic operations, its practical uses in everyday situations, and its role in more advanced mathematical concepts. Mastering division is not just about getting the right answer; it's about understanding the underlying principles and building a strong foundation for further mathematical exploration. The ability to break down complex problems into smaller, manageable parts, as division teaches us, is a valuable skill applicable far beyond the realm of mathematics.
Latest Posts
Latest Posts
-
85 Mins In Hours
Sep 17, 2025
-
Dichotomous Key For Animals
Sep 17, 2025
-
183 Cm To In
Sep 17, 2025
-
1 4 Divided By 2
Sep 17, 2025
-
Elements In Ammonium Chloride
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 36 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.