4 X 3 16
renascent
Sep 22, 2025 · 6 min read
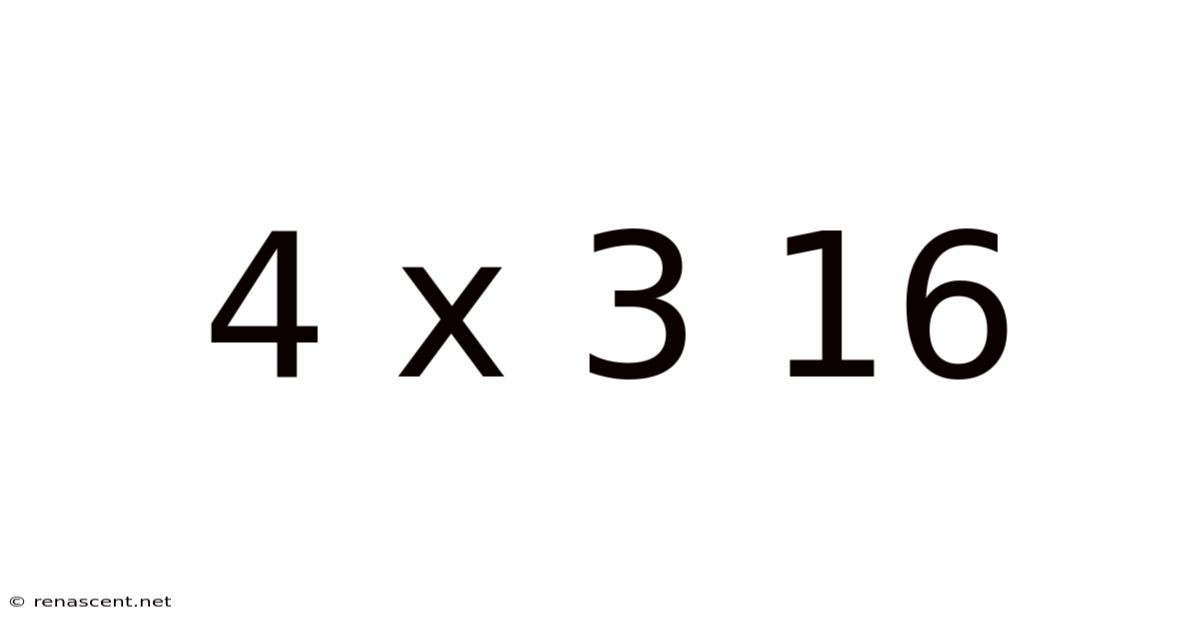
Table of Contents
Decoding 4 x 3 = 16: Exploring Non-Standard Mathematical Systems
The seemingly simple equation "4 x 3 = 16" immediately clashes with our ingrained understanding of basic arithmetic. In standard mathematics, 4 multiplied by 3 unequivocally equals 12. However, this seemingly incorrect equation opens a fascinating door to exploring alternative mathematical systems and the underlying logic that governs them. This article delves into the possibilities behind this non-standard result, examining different perspectives and revealing the rich tapestry of mathematical thought beyond the familiar. Understanding this seemingly erroneous equation allows us to appreciate the flexibility and creativity inherent within mathematics.
Introduction: Beyond Standard Arithmetic
Our initial reaction to "4 x 3 = 16" is likely disbelief. This is because we are conditioned to operate within the framework of standard base-10 arithmetic. In this system, multiplication represents repeated addition. Therefore, 4 x 3 means adding four three times (3 + 3 + 3 + 3 = 12). The statement "4 x 3 = 16" directly contradicts this fundamental principle.
However, the beauty of mathematics lies in its ability to adapt and evolve. Many mathematical systems exist beyond the standard arithmetic we learn in school. These systems may operate under different rules, axioms, and definitions, leading to results that appear counterintuitive within our familiar framework. The equation "4 x 3 = 16" can be explained within the context of such alternative systems.
Possible Explanations for 4 x 3 = 16
Several scenarios could potentially lead to the result 4 x 3 = 16. Let's explore some possibilities:
1. Non-Standard Number Systems:
-
Modular Arithmetic: Modular arithmetic operates within a specific modulus. This means that the results "wrap around" after reaching a certain value. For example, in modulo 5 arithmetic (mod 5), any number divisible by 5 becomes 0. While it's not possible to directly obtain 16 through simple modular arithmetic to get a result of 16 from 4 x 3, more complex modular systems combined with other operations could potentially generate such a result. However, this would require a carefully designed system of operations beyond simple multiplication.
-
Base-n Number Systems: We are accustomed to the base-10 number system (decimal). Other bases exist, such as binary (base-2), hexadecimal (base-16), and others. Changing the base of the numbers involved could theoretically manipulate the outcome. However, a simple change of base alone would not directly produce 16 from 4 x 3. A combination of base changes and redefined arithmetic operations might be necessary.
2. Redefined Arithmetic Operations:
-
Modified Multiplication: The core of the problem lies in the redefinition of the multiplication operation itself. Standard multiplication involves repeated addition. However, if we redefine multiplication to incorporate other operations or factors, we can potentially reach the result 16. For example, one could create a new operation denoted as "*" where a * b = (a + b) + (a x b). Using this, 4 * 3 = (4 + 3) + (4 x 3) = 7 + 12 = 19. This still doesn't produce 16, but this illustrates the concept of redefining operations to produce non-standard results. More complex, custom-defined operations could indeed result in 4 x 3 = 16.
-
Hidden Operations: The equation might be concealing additional operations. For instance, the equation might represent a sequence of operations disguised as a simple multiplication.
3. Contextual Interpretation:
-
Symbolic Representation: The equation could be a symbolic representation within a specific mathematical framework, where 'x' and '=' may not represent standard multiplication and equality. This interpretation moves beyond arithmetic and delves into abstract algebra and symbolic logic. The symbols could be defined within a system to yield the desired outcome.
-
Encoded Message: In a playful or puzzle context, "4 x 3 = 16" could be a coded message, where the equation itself isn't meant to be solved literally. The numbers or symbols could possess hidden meanings within the context of a larger riddle.
Constructing a System Where 4 x 3 = 16
Let's explore a hypothetical system where 4 x 3 = 16 is a valid statement. We'll need to redefine at least one of the components:
- Redefining Multiplication: Let's introduce a new operation, denoted as ⊕, such that a ⊕ b = (a + b) + (a * b) – 2 * (min(a, b)) where * represents standard multiplication and min(a,b) denotes the minimum value between 'a' and 'b'.
Let's test this:
4 ⊕ 3 = (4 + 3) + (4 * 3) – 2 * min(4,3) = 7 + 12 – 2 * 3 = 19 – 6 = 13. This is not 16.
Now, let's try another operation ⊗ where a ⊗ b = (a + b)^2 / (a + b -1)
4 ⊗ 3 = (4+3)^2 / (4+3-1) = 49/6 = 8.16...
Still, no result of 16.
To achieve 4 x 3 = 16, a more complex and potentially less intuitive operation would be needed. The difficulty here emphasizes the point that deriving "4 x 3 = 16" necessitates a radical departure from standard arithmetic.
The Importance of Defining Axioms and Rules
This exercise highlights the critical role of axioms and rules in defining any mathematical system. In standard arithmetic, the commutative, associative, and distributive properties govern operations. However, for "4 x 3 = 16" to hold true, a completely new set of axioms and rules would need to be defined. These rules would define how numbers interact under the operations of addition and multiplication within this novel system. Without explicitly stating these new rules, the equation remains illogical within the commonly accepted framework of mathematics.
Frequently Asked Questions (FAQ)
Q: Is there any real-world application where 4 x 3 = 16 could be valid?
A: In standard arithmetic, no. The equation is only valid within specifically designed mathematical systems. These systems might have theoretical uses within abstract algebra or advanced computer science. However, it is unlikely to find a direct, practical application in everyday calculations.
Q: Could this equation be used in a puzzle or riddle?
A: Yes, absolutely. The equation could be a clue in a puzzle that requires lateral thinking and understanding that a different set of rules is in play.
Q: Is it mathematically wrong to say 4 x 3 = 16?
A: It's not wrong within a carefully defined system. Within standard arithmetic, it's incorrect. However, the possibility of creating a system where this statement holds true underscores the richness and flexibility of mathematics.
Q: Why is it important to understand non-standard mathematical systems?
A: Understanding non-standard systems broadens our perspective on mathematics. It demonstrates that mathematics is not a rigid set of rules but a dynamic and evolving field where creativity and innovation are key. This helps develop critical thinking skills and opens possibilities for future breakthroughs in abstract mathematics and computing.
Conclusion: Expanding Mathematical Horizons
The exploration of "4 x 3 = 16" serves as a compelling reminder that the world of mathematics extends far beyond the familiar rules of elementary arithmetic. While this equation contradicts standard arithmetic, it opens exciting avenues for considering alternate mathematical frameworks. By constructing hypothetical systems where this statement could be valid, we gain a deeper appreciation for the flexible nature of mathematics and the importance of clearly defining axioms and operations. This journey into non-standard mathematics encourages critical thinking, problem-solving skills, and a richer understanding of the underlying principles that govern the world of numbers. The seemingly simple equation acts as a gateway to a much wider and more complex world of mathematical possibilities. It's a testament to the creativity and power of mathematical thought.
Latest Posts
Latest Posts
-
Decimal Of 3 8
Sep 22, 2025
-
Equation For Semicircle Graph
Sep 22, 2025
-
1 6k Usd To Aud
Sep 22, 2025
-
7 Elements Of Drama
Sep 22, 2025
-
Meaning Of Extensive Farming
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 4 X 3 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.