48 Divided By 5
renascent
Sep 22, 2025 · 6 min read
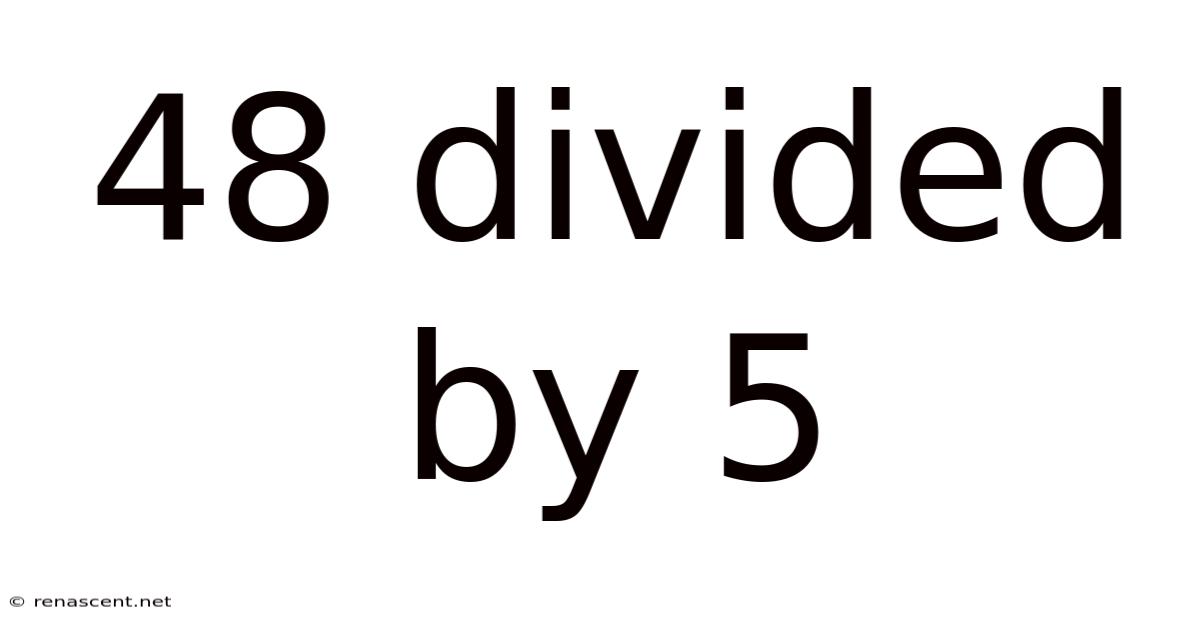
Table of Contents
Unveiling the Mystery: 48 Divided by 5 – A Deep Dive into Division
Dividing 48 by 5 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation provides a rich opportunity to explore fundamental mathematical concepts, delve into different methods of solving the problem, and understand the underlying principles of division. This article will go beyond a simple answer, offering a comprehensive exploration of 48 ÷ 5, catering to readers of all levels, from beginners grasping the basics of division to those seeking a deeper understanding of mathematical processes.
Understanding Division: The Basics
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a whole number (the dividend) into equal parts, with the number of parts determined by another number (the divisor). The result of the division is called the quotient. In our case, 48 is the dividend and 5 is the divisor. We want to find out how many times 5 fits into 48 and what remains.
Method 1: Long Division – The Classic Approach
Long division is a traditional and widely used method for performing division, especially with larger numbers. Let's break down how to solve 48 ÷ 5 using this method:
-
Set up the problem: Write the dividend (48) inside the long division symbol (⟌) and the divisor (5) outside.
5⟌48 -
Divide the tens digit: How many times does 5 go into 4? It doesn't go in at all, so we move to the next digit.
-
Divide the tens and units digits: How many times does 5 go into 48? It goes in 9 times (5 x 9 = 45). Write the 9 above the 8 (the units digit of the dividend).
9 5⟌48 -
Multiply and subtract: Multiply the quotient (9) by the divisor (5): 9 x 5 = 45. Write 45 below the 48 and subtract: 48 - 45 = 3.
9 5⟌48 45 -- 3 -
The Remainder: The 3 is the remainder. This signifies that after dividing 48 into groups of 5, we have 3 left over.
Therefore, 48 ÷ 5 = 9 with a remainder of 3. This can also be expressed as a mixed number: 9 3/5. The 9 represents the whole number of times 5 fits into 48, and the 3/5 represents the remaining fraction.
Method 2: Repeated Subtraction – A Visual Approach
Repeated subtraction offers a more visual and intuitive way to understand division, especially for beginners. It involves repeatedly subtracting the divisor from the dividend until the result is less than the divisor. Let's see how it works for 48 ÷ 5:
-
Start with the dividend: Begin with 48.
-
Repeatedly subtract the divisor: Subtract 5 repeatedly:
- 48 - 5 = 43
- 43 - 5 = 38
- 38 - 5 = 33
- 33 - 5 = 28
- 28 - 5 = 23
- 23 - 5 = 18
- 18 - 5 = 13
- 13 - 5 = 8
- 8 - 5 = 3
-
Count the subtractions: We subtracted 5 a total of 9 times.
-
The remainder: The final result, 3, is the remainder.
Again, we arrive at the same answer: 48 ÷ 5 = 9 with a remainder of 3 or 9 3/5.
Method 3: Using Decimals – Beyond Whole Numbers
While long division and repeated subtraction provide answers with remainders, we can also express the answer using decimals. This involves continuing the division process beyond the whole number quotient.
-
Add a decimal point and zeros: After obtaining the remainder 3, add a decimal point to the dividend (48) and add zeros as needed.
9. 5⟌48.00 45 -- 30 -
Continue the division: Now, divide 30 by 5. 5 goes into 30 six times (5 x 6 = 30).
9.6 5⟌48.00 45 -- 30 30 -- 0
Therefore, 48 ÷ 5 = 9.6. This decimal representation shows that 48 can be divided into 5 equal parts of 9.6 each.
The Significance of Remainders and Decimals
The remainder (3 in this case) has practical significance. It represents the portion that cannot be equally divided among the 5 groups. For example, if you have 48 candies and want to distribute them equally among 5 friends, each friend gets 9 candies, and you'll have 3 candies left over.
The decimal representation (9.6) provides a more precise answer, indicating the exact value of each equal part. This is useful in situations where fractions or remainders are impractical or undesirable. For instance, if you're dividing a length of 48 centimeters into 5 equal segments, each segment would be 9.6 centimeters long.
Exploring Further: Applications and Extensions
Understanding 48 ÷ 5 transcends simple arithmetic. The concepts illustrated here have broader applications:
-
Fractions and Decimals: This problem reinforces the relationship between fractions (3/5) and decimals (0.6).
-
Real-World Applications: Division is fundamental in various fields like engineering (calculating dimensions), finance (sharing costs), and computer science (data allocation).
-
Advanced Math: The concept of remainders is crucial in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Problem-solving: Breaking down a complex problem into smaller, manageable steps (as shown in the long division method) is a valuable problem-solving skill applicable beyond mathematics.
Frequently Asked Questions (FAQ)
-
Q: What is the most efficient method to divide 48 by 5?
A: The most efficient method depends on your comfort level and the context. For quick mental calculation, repeated subtraction can be helpful. For larger numbers or increased precision, long division is preferred. If a decimal answer is needed, the decimal long division method is the most accurate.
-
Q: What if the remainder is larger than the divisor?
A: If the remainder is larger than the divisor, it means there's an error in the division process. The quotient needs to be increased.
-
Q: Can I use a calculator to solve 48 ÷ 5?
A: Yes, calculators provide a quick and accurate solution. However, understanding the underlying methods is crucial for grasping the mathematical concepts involved.
-
Q: Why are there different ways to solve the same problem?
A: Different methods offer various perspectives and levels of understanding. Choosing the appropriate method depends on the situation, the available tools, and the desired level of precision.
Conclusion: Beyond the Numbers
Solving 48 ÷ 5 goes beyond simply getting the answer of 9 with a remainder of 3 or 9.6. The process provides an excellent platform to understand the core principles of division, explore different calculation methods, and appreciate the versatility of mathematical concepts. The ability to perform division and interpret the results is a fundamental skill with far-reaching applications in various fields. This deep dive into a seemingly simple problem demonstrates the richness and depth inherent in even the most basic mathematical operations, encouraging further exploration and a deeper appreciation of the beauty and power of mathematics. By understanding the different approaches and their implications, you'll not only be able to solve this particular problem but also confidently tackle more complex division problems in the future.
Latest Posts
Latest Posts
-
Meaning Of Extensive Farming
Sep 22, 2025
-
50 Digits Of Pi
Sep 22, 2025
-
Biotic Factors Of Grassland
Sep 22, 2025
-
1 3 Divided By 1
Sep 22, 2025
-
Disadvantages Of Selective Breeding
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 48 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.