1/3 Divided By 1
renascent
Sep 22, 2025 · 5 min read
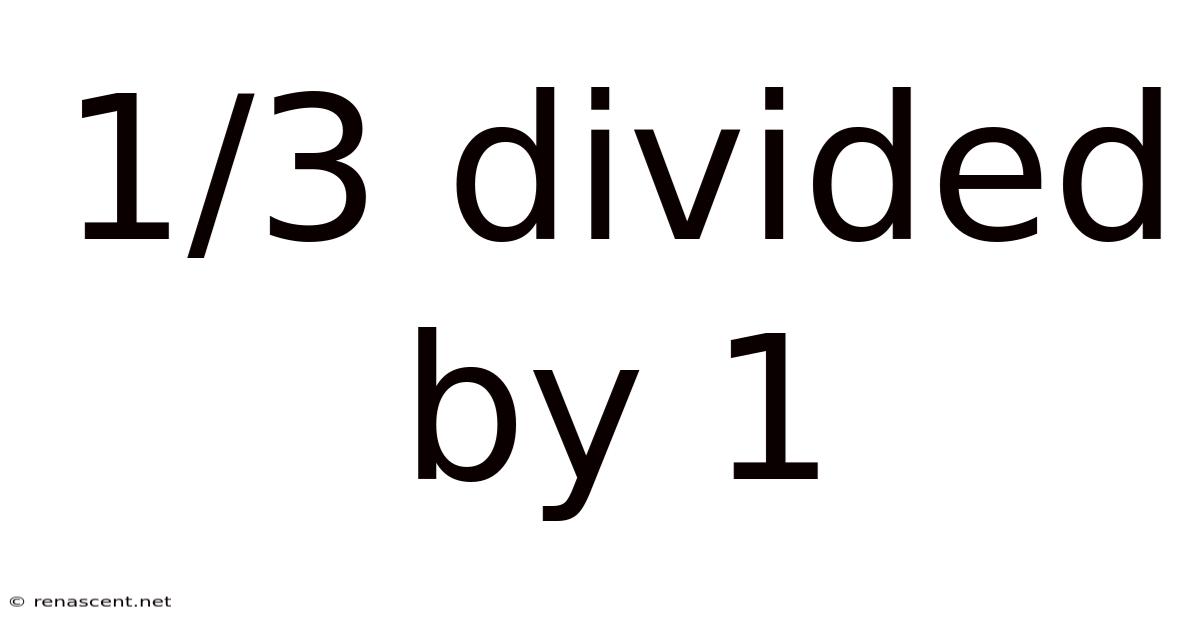
Table of Contents
Understanding 1/3 Divided by 1: A Comprehensive Guide
This article will explore the seemingly simple mathematical operation of dividing one-third (1/3) by one (1). While the answer might seem obvious at first glance, a deeper understanding reveals fundamental concepts in fractions and division that are crucial for mastering more complex mathematical problems. We'll break down the process step-by-step, explore the underlying principles, and address frequently asked questions. This guide is perfect for anyone looking to solidify their understanding of fractions and division, from elementary school students to adults brushing up on their math skills.
Understanding Fractions: The Building Blocks
Before diving into the division problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our case, 1/3 means we have one part out of a whole that's divided into three equal parts. Understanding this basic structure is critical for grasping fraction division.
Dividing Fractions: The Key Concepts
Dividing by 1 is a unique operation. Any number divided by 1 remains unchanged. This is because division essentially asks, "How many times does the divisor (the number you're dividing by) fit into the dividend (the number being divided)?" Since 1 fits into any number exactly that number of times, the result is always the same as the dividend.
This principle holds true for fractions as well. When we divide a fraction by 1, the fraction remains the same.
Step-by-Step Solution: 1/3 ÷ 1
Let's approach the problem 1/3 ÷ 1 systematically:
-
Identify the dividend and divisor: The dividend is 1/3, and the divisor is 1.
-
Apply the division principle: We're asking, "How many times does 1 fit into 1/3?" The answer is 1/3. One whole (1) fits into one-third (1/3) exactly one-third of a time.
-
Result: Therefore, 1/3 ÷ 1 = 1/3.
The fraction remains unchanged because dividing by 1 doesn't alter the quantity.
Illustrative Examples: Visualizing Fraction Division
Let's visualize this with a few real-world examples:
-
Imagine a pizza: You have one-third (1/3) of a pizza. If you divide that one-third into one equal portion, you still have one-third (1/3) of a pizza.
-
Think of a chocolate bar: You have one-third (1/3) of a chocolate bar. Dividing that one-third into one piece doesn't change the amount of chocolate you have; you still possess one-third (1/3).
These examples show that dividing a fraction (like 1/3) by 1 always results in the original fraction. This isn't a complex mathematical manipulation; it reflects the fundamental nature of division by one.
Expanding the Concept: Dividing Fractions by Other Numbers
While dividing by 1 simplifies the problem, understanding how to divide fractions by other numbers is essential. Here's a brief overview:
To divide a fraction by another fraction, we use the reciprocal method:
-
Find the reciprocal of the divisor: The reciprocal of a fraction is obtained by switching its numerator and denominator. For example, the reciprocal of 2/3 is 3/2.
-
Multiply the dividend by the reciprocal of the divisor: Instead of dividing by the fraction, multiply by its reciprocal.
Example: 1/3 ÷ 2/3 = 1/3 * 3/2 = 3/6 = 1/2
In this example, we multiplied 1/3 by the reciprocal of 2/3, which is 3/2. The result is 1/2. This method provides a consistent approach for dividing fractions.
The Importance of Understanding Division by 1
The seemingly trivial case of dividing by 1 actually highlights a crucial concept in mathematics: the identity property of division. This property states that any number divided by 1 remains the same. This seemingly simple rule forms a foundation for more complex mathematical operations and serves as a building block for deeper understanding.
Addressing Frequently Asked Questions (FAQs)
Q1: Why doesn't dividing 1/3 by 1 change the value?
A1: Dividing by 1 means you're essentially splitting the quantity into one equal part. Splitting something into one part leaves it unchanged. This is a fundamental property of division.
Q2: Is there a difference between dividing a fraction by 1 and multiplying a fraction by 1?
A2: Yes, there's a difference. Dividing by 1 leaves the fraction unchanged, while multiplying by 1 also leaves the fraction unchanged. However, division is the inverse operation of multiplication. While the results are the same in this specific case, the processes are distinct.
Q3: How can I explain this concept to a child?
A3: Use real-world objects. Imagine a chocolate bar divided into three pieces. If you have one piece (1/3), and you divide that one piece into just one portion, you still have one piece (1/3). You haven't changed the amount.
Q4: Can we apply the same principle to other numbers besides fractions?
A4: Absolutely! The principle that dividing any number by 1 results in the same number applies to all numbers, whether they are whole numbers, decimals, or fractions.
Conclusion: Mastering the Fundamentals
Dividing 1/3 by 1, while seemingly simple, unveils crucial concepts within fraction division and the broader mathematical landscape. Understanding the identity property of division and the process of dividing fractions by other numbers lays a solid foundation for tackling more complex problems. Mastering these fundamentals is key to developing a strong mathematical foundation and confidently approaching more advanced topics. By understanding the underlying principles and applying the steps outlined in this guide, you can approach any fraction division problem with greater confidence and clarity. Remember to visualize the problem, use real-world examples, and practice regularly to solidify your understanding. With consistent effort and a clear understanding of the core concepts, success in mathematics is within your reach.
Latest Posts
Latest Posts
-
Does Alcohol Kill Mold
Sep 22, 2025
-
Do Catfish Have Teeth
Sep 22, 2025
-
3500 Divided By 100
Sep 22, 2025
-
7 10 As A Decimal
Sep 22, 2025
-
6 20 As A Percentage
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1/3 Divided By 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.