4x X 2 4
renascent
Sep 21, 2025 · 5 min read
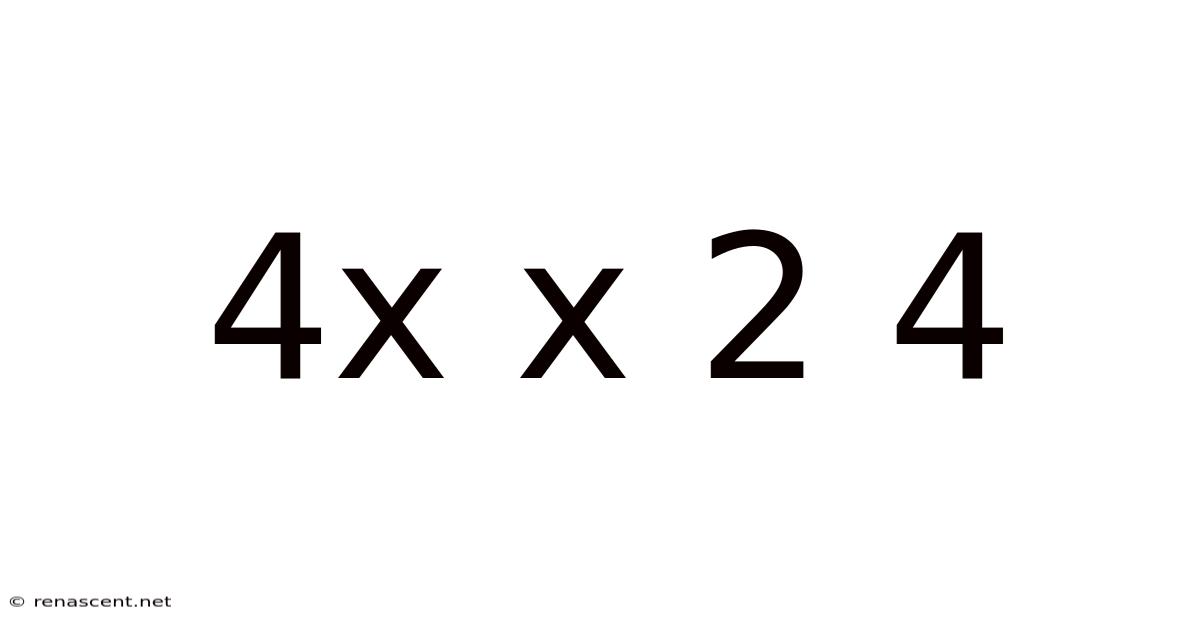
Table of Contents
Decoding 4x x 2^4: Exploring Exponential Growth and its Applications
This article delves into the mathematical expression "4x x 2^4," explaining its components, calculating its value, and exploring its relevance in various fields, including exponential growth, computer science, and finance. We'll break down the concept step-by-step, ensuring a clear understanding, regardless of your mathematical background. Understanding this seemingly simple equation provides a gateway to grasping more complex mathematical concepts and their real-world applications.
Introduction: Understanding the Components
The expression "4x x 2^4" involves several key mathematical elements:
-
4x: This represents a variable expression, where 'x' is an unknown value multiplied by 4. The value of this part of the equation is dependent on the value of 'x'.
-
x: This is a variable, representing an unknown number or quantity. It could be any real number (positive, negative, or zero).
-
2^4: This is an exponential expression. It means 2 multiplied by itself four times (2 x 2 x 2 x 2). This simplifies to 16.
-
x: The multiplication symbol signifies the operation of multiplication between the terms.
Calculating the Value: A Step-by-Step Approach
To calculate the value of "4x x 2^4," we first simplify the exponential term:
-
Simplify the exponent: 2^4 = 16
-
Substitute: Replace 2^4 with its simplified value of 16 in the original expression: 4x x 16
-
Simplify the multiplication: 4x x 16 = 64x
Therefore, the simplified form of the expression "4x x 2^4" is 64x. The final value depends entirely on the value assigned to the variable 'x'. For example:
- If x = 1, then 64x = 64
- If x = 2, then 64x = 128
- If x = 0, then 64x = 0
- If x = -1, then 64x = -64
Understanding Exponential Growth
The presence of 2^4 highlights the concept of exponential growth. Exponential growth occurs when a quantity increases by a fixed percentage over time. In this case, the base (2) represents the growth factor, and the exponent (4) represents the number of periods of growth.
Imagine a population of bacteria doubling every hour. If we start with 2 bacteria (x=2), after 4 hours (the exponent), the population would be calculated using a similar principle: 2 x 2^4 = 32 bacteria. The expression 4x x 2^4, while not directly modeling population growth in this exact scenario, exemplifies the fundamental mathematical principle behind exponential increases.
Applications in Various Fields
The principles illustrated by the expression 4x x 2^4 have widespread applications across diverse fields:
-
Computer Science: Binary systems, the foundation of computer operation, rely on powers of 2. Memory allocation, data transfer rates, and algorithm complexities frequently involve calculations similar to 2^4, representing the exponential growth in computational power or data size. The '4x' component might represent a factor like the number of processors or the efficiency of a particular algorithm.
-
Finance: Compound interest calculations utilize exponential growth. The expression could be adapted to model the growth of an investment where 'x' represents the initial investment, '4' a constant factor, and 2^4 the compounding effect over a certain period (4 periods). The larger the exponent, the more significant the impact of compounding.
-
Physics and Engineering: Exponential decay and growth are prevalent in various physical phenomena, like radioactive decay (half-life calculations), capacitor discharge, and population dynamics (in ecology). The expression, with appropriate adjustments, could be used to model these scenarios.
-
Biology: Bacterial growth, as mentioned earlier, is a prime example of exponential growth. Similarly, the spread of viruses or the growth of certain populations can be modeled using exponential functions.
Solving Equations with Exponential Terms
Understanding the expression 4x x 2^4 is a stepping stone towards solving more complex equations involving exponential terms. Consider the following example:
64x = 128
To solve for x, we would divide both sides of the equation by 64:
x = 128 / 64 = 2
This demonstrates how the simplified expression (64x) can be used in solving equations.
Expanding the Concept: More Complex Scenarios
We can extend this understanding to more complex scenarios involving multiple variables and exponents. For instance, consider the expression:
(2x + 5) x 3^3
Here, we'd first calculate 3^3 (27), then substitute and simplify the expression:
(2x + 5) x 27 = 54x + 135
This example shows how the basic principles of simplification and substitution, learned from analyzing 4x x 2^4, can be applied to more sophisticated mathematical expressions.
Frequently Asked Questions (FAQ)
-
What happens if 'x' is a negative number? If 'x' is negative, the result (64x) will also be negative. This is because a positive number multiplied by a negative number always yields a negative result.
-
Can we simplify 4x x 2^4 further if we don't know the value of 'x'? No, we cannot simplify it further without knowing the value of 'x'. 64x is the simplest form of the expression.
-
What are some real-world applications beyond those mentioned? Many fields use exponential functions; examples include chemical reactions (rate laws), heat transfer, and the spread of information or rumors (social sciences).
-
How does this relate to logarithmic functions? Logarithmic functions are the inverse of exponential functions. If we were given an equation like 64x = y, we could use a logarithm to solve for x if we knew the value of y.
Conclusion: A Foundation for Further Learning
The seemingly simple expression "4x x 2^4," through its simplification to 64x, provides a valuable introduction to several fundamental mathematical concepts, most notably exponential growth and its implications. Understanding this expression helps build a strong foundation for tackling more advanced mathematical problems in various fields. By breaking down the components, understanding the calculation process, and exploring its applications, we’ve not only solved the expression but also gained a deeper appreciation for the power of exponential relationships in the world around us. The key takeaway is the ability to simplify complex expressions into more manageable forms, revealing the underlying mathematical structure and enabling us to apply these principles to a wide array of real-world problems.
Latest Posts
Latest Posts
-
70ml To Grams Powder
Sep 21, 2025
-
90 Percent Of 27
Sep 21, 2025
-
98 7 F To C
Sep 21, 2025
-
Banana And Sprite Challenge
Sep 21, 2025
-
Hydrogen Bromide Lewis Structure
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 4x X 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.