90 Percent Of 27
renascent
Sep 21, 2025 · 5 min read
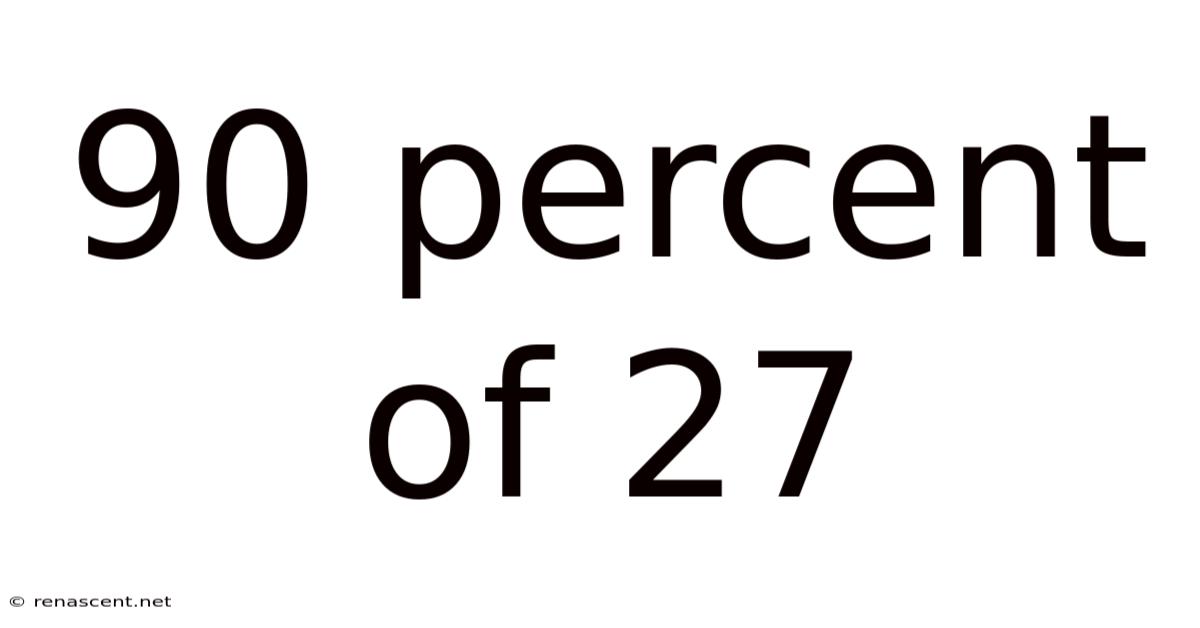
Table of Contents
Unveiling the Mystery: 90 Percent of 27 – A Deep Dive into Percentages and Their Applications
Finding 90% of 27 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to calculate percentages, and the underlying concepts, is crucial for numerous applications in everyday life, from calculating discounts and taxes to understanding financial statements and interpreting statistical data. This article will not only show you how to calculate 90% of 27 but also explore the broader implications of percentage calculations and their real-world relevance. We'll delve into the methods, the reasoning, and practical examples to solidify your understanding.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 90% can be written as 90/100, or as a decimal, 0.9. This simple conversion is the key to unlocking percentage calculations.
Method 1: Converting to a Decimal
This is arguably the most straightforward method for finding 90% of 27.
-
Convert the percentage to a decimal: Divide 90 by 100: 90 ÷ 100 = 0.9
-
Multiply the decimal by the number: Multiply 0.9 by 27: 0.9 x 27 = 24.3
Therefore, 90% of 27 is 24.3.
This method leverages the fundamental understanding of percentages as fractions of 100. By converting the percentage to its decimal equivalent, we directly translate the problem into a simple multiplication problem. This method is efficient and easily adaptable to calculating any percentage of any number.
Method 2: Using Fractions
This method offers a slightly different perspective, reinforcing the fractional nature of percentages.
-
Convert the percentage to a fraction: 90% can be written as 90/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 10. This simplifies to 9/10.
-
Multiply the fraction by the number: Multiply 9/10 by 27: (9/10) x 27 = 243/10
-
Convert the improper fraction to a decimal: Divide 243 by 10: 243 ÷ 10 = 24.3
Again, we arrive at the answer: 90% of 27 is 24.3.
This method highlights the interchangeability between percentages, decimals, and fractions, emphasizing the interconnectedness of these mathematical concepts. It's particularly useful when dealing with percentages that have simple fractional equivalents, allowing for easier mental calculations in certain scenarios.
Method 3: Proportion Method
This method is less direct but provides a clearer understanding of the underlying proportional relationship.
We can set up a proportion:
Let x represent 90% of 27.
90/100 = x/27
To solve for x, we cross-multiply:
90 * 27 = 100 * x
2430 = 100x
x = 2430 / 100
x = 24.3
Therefore, 90% of 27 is 24.3.
This method demonstrates the proportional relationship between the percentage and the resulting part of the whole. It's a powerful technique that can be applied to a wide range of proportional problems beyond simple percentage calculations.
Real-World Applications: Where Percentages Matter
The seemingly simple calculation of 90% of 27 finds its application in a vast array of real-world scenarios. Here are just a few examples:
-
Sales and Discounts: Imagine a store offering a 90% discount on an item originally priced at $27. Using our calculation, the discount amount would be $24.30, and the final price would be $27 - $24.30 = $2.70.
-
Taxes: If a 90% tax (a highly unusual scenario, but illustrative) were applied to a $27 purchase, the tax amount would be $24.30, resulting in a total cost of $51.30.
-
Statistics and Data Analysis: Percentages are fundamental to understanding and interpreting statistical data. For instance, if 90% of 27 participants in a survey responded positively to a question, it indicates a strong positive response rate.
-
Financial Statements: Financial reports heavily rely on percentage calculations to present data in a meaningful and comparable way. Profit margins, growth rates, and debt ratios are all expressed as percentages.
-
Grade Calculations: Many grading systems use percentages to represent a student's performance. If a student scores 90% on a 27-point test, their score would be 24.3 points.
These examples demonstrate that the ability to calculate percentages isn't just an academic exercise; it's a practical skill with far-reaching consequences across various domains.
Beyond the Basics: Expanding Your Percentage Knowledge
While calculating 90% of 27 is straightforward, a deeper understanding of percentages involves more than just simple calculations. This includes:
-
Understanding Percentage Change: This involves calculating the increase or decrease in a value as a percentage. For example, if a value increases from 20 to 27, the percentage change would be calculated as [(27-20)/20] * 100% = 35%.
-
Working with Compound Percentages: These involve calculating successive percentage changes. For instance, a 10% increase followed by a 20% increase does not equal a 30% increase.
-
Understanding Percentage Points: This is a crucial distinction. A change from 20% to 30% is a 10 percentage point increase, not a 50% increase.
Mastering these concepts expands the practical applications of percentages significantly.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator for this?
A: Absolutely! Calculators are efficient tools for performing these calculations, particularly when dealing with more complex percentages or larger numbers.
Q: What if the percentage isn't a whole number, such as 90.5%?
A: The same methods apply. Convert 90.5% to a decimal (0.905) and multiply by 27.
Q: Are there any online tools to calculate percentages?
A: Yes, numerous online percentage calculators are available. These can be helpful for quick calculations and verification.
Q: What if I need to find the percentage one number represents of another?
A: To find what percentage a number (say, 24.3) represents of another number (27), you would divide the first number by the second and multiply by 100: (24.3/27) * 100% = 90%.
Conclusion: Mastering Percentages for a Brighter Future
The ability to calculate percentages is an invaluable life skill. Understanding the underlying principles, whether using decimal conversion, the fraction method, or proportions, unlocks a world of applications far beyond simple arithmetic problems. From navigating everyday finances to understanding complex statistical analyses, proficiency in percentage calculations empowers you to make informed decisions and contribute effectively in numerous areas of life. So, the next time you encounter a percentage problem, remember the fundamental principles outlined in this article and approach it with confidence. You've already mastered 90% of 27 – now go conquer the world of percentages!
Latest Posts
Latest Posts
-
210 F To C
Sep 21, 2025
-
3 X 1 2
Sep 21, 2025
-
Absolute Or Gauge Pressure
Sep 21, 2025
-
Four Letter American States
Sep 21, 2025
-
Advantages Of A Franchise
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 90 Percent Of 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.