5/12 As A Decimal
renascent
Sep 22, 2025 · 5 min read
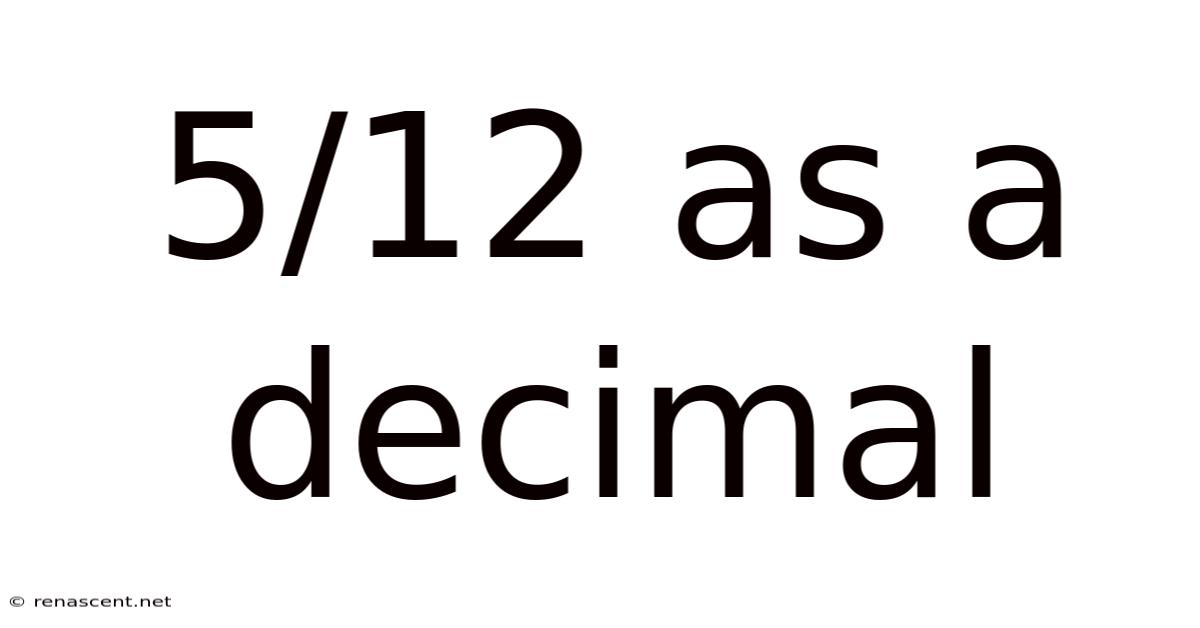
Table of Contents
Understanding 5/12 as a Decimal: A Comprehensive Guide
Fractions and decimals are fundamental concepts in mathematics, representing parts of a whole. Converting between these forms is a crucial skill, and this article will provide a thorough explanation of how to convert the fraction 5/12 into its decimal equivalent. We'll explore multiple methods, delve into the underlying mathematical principles, and address frequently asked questions. Understanding this process will strengthen your foundation in arithmetic and improve your problem-solving abilities.
Understanding Fractions and Decimals
Before we dive into the conversion, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, in the fraction 5/12, 5 is the numerator and 12 is the denominator. This means we're considering 5 out of 12 equal parts.
A decimal, on the other hand, represents a part of a whole using a base-10 system. The decimal point separates the whole number part from the fractional part. Each position to the right of the decimal point represents a power of 10: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (5) by the denominator (12).
-
Set up the long division: Write 5 as the dividend (inside the division symbol) and 12 as the divisor (outside the division symbol). Add a decimal point to the dividend (5) and add zeros as needed to continue the division.
____ 12|5.0000 -
Perform the division: 12 does not go into 5, so we add a zero and a decimal point to the quotient. 12 goes into 50 four times (12 x 4 = 48). Subtract 48 from 50, leaving a remainder of 2.
0.4 12|5.0000 48 2 -
Continue the process: Bring down the next zero (making it 20). 12 goes into 20 one time (12 x 1 = 12). Subtract 12 from 20, leaving a remainder of 8.
0.41 12|5.0000 48 20 12 8 -
Repeat: Bring down another zero (making it 80). 12 goes into 80 six times (12 x 6 = 72). Subtract 72 from 80, leaving a remainder of 8.
0.416 12|5.0000 48 20 12 80 72 8 -
Observe the pattern: Notice that we keep getting a remainder of 8. This indicates a repeating decimal. The digits "6" will repeat indefinitely.
Therefore, 5/12 as a decimal is 0.416666... This is often written as 0.416̅, with a bar over the repeating digit.
Method 2: Converting to an Equivalent Fraction with a Denominator of a Power of 10
While long division is reliable, this method isn't always practical, especially with complex fractions. Ideally, we would convert the denominator to a power of 10 (10, 100, 1000, etc.). Unfortunately, 12 cannot be easily converted to a power of 10 because its prime factorization is 2 x 2 x 3. There isn't a simple way to multiply 12 by an integer to get a power of 10. This method is less effective for 5/12.
Understanding Repeating Decimals
The decimal representation of 5/12 (0.416̅) is a repeating decimal. This means that the decimal representation has a sequence of digits that repeat infinitely. Understanding why this happens is important. It's because the denominator (12) contains prime factors other than 2 and 5 (it contains a 3). Fractions with denominators containing only prime factors of 2 and 5 always terminate (end) as decimals. Other fractions will result in repeating decimals.
Applications of Decimal Conversion
The ability to convert fractions to decimals is crucial in various applications:
- Financial Calculations: Dealing with percentages, interest rates, and monetary values often requires converting fractions to decimals.
- Scientific Measurements: Many scientific instruments provide readings in decimal form.
- Engineering and Construction: Precision in calculations is essential in these fields, often requiring converting fractions to decimals for accuracy.
- Data Analysis: Converting fractions to decimals facilitates data analysis and statistical calculations.
- Everyday Life: Converting fractions to decimals can make understanding proportions and ratios easier in everyday situations, like splitting a bill or measuring ingredients.
Frequently Asked Questions (FAQ)
-
Q: Can all fractions be converted to decimals?
A: Yes, all fractions can be converted to decimals. However, the resulting decimal may be terminating (ending) or repeating (non-terminating).
-
Q: What if I get a very long repeating decimal? How do I round it?
A: When dealing with long repeating decimals in practical applications, you'll often need to round the decimal to a specific number of decimal places. The standard rule is to round up if the next digit is 5 or greater, and round down if it's less than 5. For example, rounding 0.416666... to three decimal places gives 0.417.
-
Q: Is there a way to know before performing the long division if a fraction will result in a repeating decimal?
A: Yes. If the denominator of the fraction, when simplified, contains prime factors other than 2 and 5, the resulting decimal will be repeating.
-
Q: Are there any other methods for converting fractions to decimals besides long division?
A: While long division is the most common and generally applicable method, some fractions can be converted mentally or using calculators. Using a calculator is often the quickest method for practical purposes. However, understanding the long division method is crucial for grasping the underlying mathematical principles.
-
Q: Why is it important to learn how to convert fractions to decimals?
A: This skill is fundamental to understanding and working with numbers in various contexts. It bridges the gap between two different ways of representing parts of a whole, making calculations and interpretations more versatile and efficient.
Conclusion
Converting the fraction 5/12 to its decimal equivalent, 0.416̅, involves applying the principle of long division. This seemingly simple process reveals a deeper understanding of fractions, decimals, and the nature of repeating decimals. By mastering this conversion, you gain a stronger foundation in mathematical concepts and practical problem-solving abilities applicable across numerous fields. Remember to practice regularly to reinforce your understanding and build confidence in your mathematical skills. The ability to effortlessly convert fractions to decimals is a testament to a solid grasp of fundamental mathematical principles.
Latest Posts
Latest Posts
-
10 X 7 8
Sep 22, 2025
-
X 1 2 Expand
Sep 22, 2025
-
82 In To Ft
Sep 22, 2025
-
1 5 Gallon In Liters
Sep 22, 2025
-
68 8 Kg To Lbs
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5/12 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.