5 6 X 20
renascent
Sep 14, 2025 · 6 min read
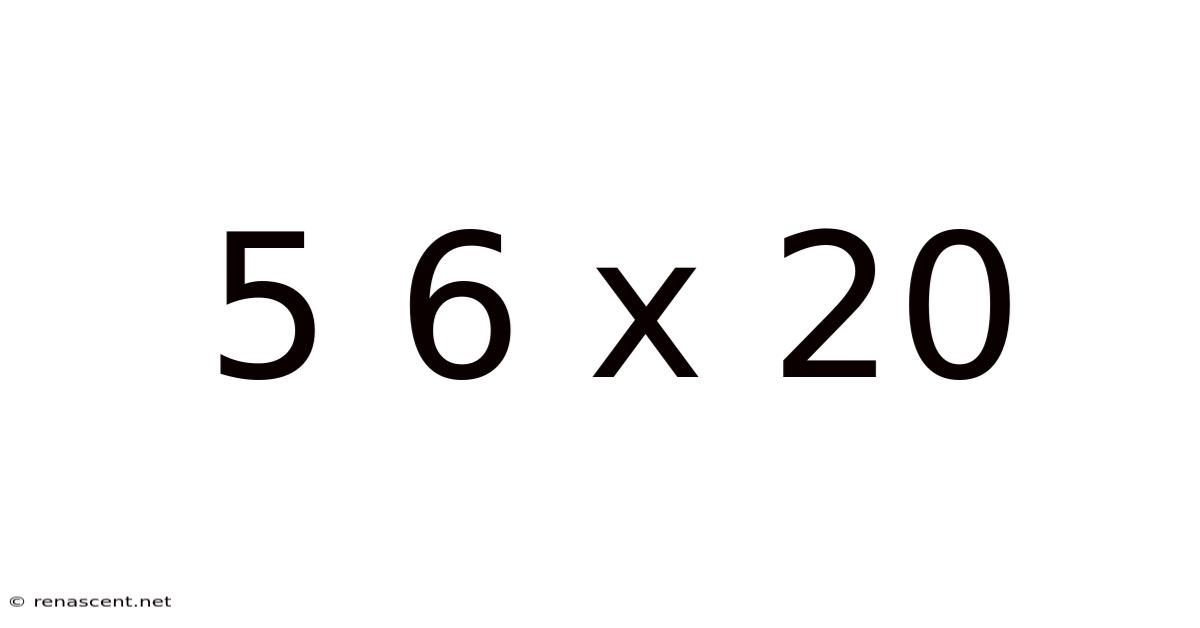
Table of Contents
Decoding 5/6 x 20: A Deep Dive into Fractions, Multiplication, and Real-World Applications
This article explores the seemingly simple mathematical expression "5/6 x 20," delving into the fundamental concepts of fractions, multiplication, and their practical applications. We'll break down the calculation step-by-step, examine different approaches to solving it, and discuss its relevance in various real-world scenarios. Understanding this seemingly basic equation is key to grasping more complex mathematical concepts later on.
Introduction: Understanding the Basics
The expression 5/6 x 20 involves the multiplication of a fraction (5/6) and a whole number (20). Before diving into the solution, let's refresh our understanding of key concepts:
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. In our example, 5/6 means we have 5 parts out of a total of 6 equal parts.
-
Multiplication: In the context of fractions, multiplication signifies finding a fraction of a whole number. In this case, we need to find what 5/6 of 20 is.
Method 1: Converting the Whole Number to a Fraction
One common method to solve this equation involves converting the whole number into a fraction. Any whole number can be expressed as a fraction with a denominator of 1. Therefore, 20 can be written as 20/1. Our equation now becomes:
(5/6) x (20/1)
To multiply fractions, we multiply the numerators together and the denominators together:
(5 x 20) / (6 x 1) = 100/6
This result, 100/6, is an improper fraction (where the numerator is larger than the denominator). We need to simplify this into a mixed number (a whole number and a proper fraction). To do this, we divide the numerator (100) by the denominator (6):
100 ÷ 6 = 16 with a remainder of 4
This means that 100/6 is equal to 16 and 4/6. We can further simplify 4/6 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2:
4/6 = 2/3
Therefore, the final answer is 16 2/3.
Method 2: Multiplying First, Then Simplifying
Alternatively, we can multiply the numerator of the fraction by the whole number first, then simplify:
5/6 x 20 = (5 x 20) / 6 = 100/6
As in Method 1, we simplify 100/6 to get 16 2/3. This method is often quicker if you're comfortable working with larger numbers.
Method 3: Simplifying Before Multiplying (Cancellation)
Before multiplying, we can simplify the equation by canceling common factors between the numerator and the denominator. Notice that 20 (in 20/1) and 6 share a common factor of 2. We can divide both 20 and 6 by 2:
(5/6) x (20/1) = (5/3) x (10/1) = 50/3
Now, we convert 50/3 to a mixed number:
50 ÷ 3 = 16 with a remainder of 2
So, 50/3 = 16 2/3. This method is particularly useful with larger numbers, making the calculation simpler.
Explanation of the Mathematical Principles Involved
The solution relies on several fundamental mathematical principles:
-
Fraction Multiplication: The core principle is the multiplication of fractions. Remember that multiplying fractions involves multiplying the numerators and multiplying the denominators separately.
-
Improper Fractions and Mixed Numbers: Understanding how to convert between improper fractions and mixed numbers is crucial for presenting the final answer in a clear and concise way.
-
Simplifying Fractions: Simplifying fractions by finding the greatest common divisor (GCD) of the numerator and denominator is essential for obtaining the most accurate and simplified answer. This process makes the fraction easier to understand and work with.
-
Order of Operations (PEMDAS/BODMAS): Although this example is straightforward, it's important to remember the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). In this case, multiplication is performed before any other operations.
Real-World Applications
The seemingly simple calculation of 5/6 x 20 has numerous practical applications in everyday life:
-
Baking and Cooking: Recipes often require fractional amounts of ingredients. For example, if a recipe calls for 5/6 of a cup of flour and you're making a recipe 20 times larger, you'd need to calculate 5/6 x 20 to determine the total amount of flour needed.
-
Construction and Engineering: Calculations involving fractions and whole numbers are fundamental in construction and engineering. Determining the amount of materials needed for a project might involve similar calculations. For example, if a certain task requires 5/6 of a unit of material per section and you need 20 sections, the total material needed would be 5/6 x 20.
-
Finance: Calculating portions of investments, discounts, or interest payments might involve fractional calculations. Imagine you have 20 shares of a company, and each share pays out 5/6 of a dollar in dividends, then the total amount received in dividends is 5/6 x 20.
-
Measurement: Whether it's measuring liquids, lengths, or weights, situations often arise where fractions need to be combined with whole numbers, mirroring this calculation. Imagine you have 20 pieces of wood that each measure 5/6 of a meter. The total length of wood will be 5/6 x 20.
-
Data Analysis: In data analysis, you may encounter scenarios involving proportions or percentages that necessitate these calculations. Suppose 5/6 of a population of 20 people share a particular characteristic. The number of people with this characteristic is found by calculating 5/6 x 20.
Frequently Asked Questions (FAQ)
-
Can I use a calculator to solve this problem? Yes, you can use a calculator, but understanding the manual calculation process is vital for grasping the underlying mathematical principles. Calculators can provide the numerical answer but won't necessarily enhance your comprehension of the process.
-
What if the fraction was a different value? The same methodology applies regardless of the specific fraction. The process involves converting the whole number to a fraction, multiplying the fractions, and then simplifying the result.
-
Why is simplifying the fraction important? Simplifying fractions is crucial for presenting the answer in its simplest and most understandable form. An unsimplified answer might be mathematically correct but less clear and user-friendly.
-
Are there other ways to solve this equation? While the methods described here are the most common and efficient, other methods, such as using decimals, might also be used. However, using decimals might introduce rounding errors in certain cases.
Conclusion: Mastering Fractions and Multiplication
Understanding the calculation of 5/6 x 20 isn't just about arriving at the answer (16 2/3); it's about understanding the underlying mathematical concepts of fractions, multiplication, simplification, and their real-world implications. Mastering these fundamental concepts is crucial for success in more advanced mathematical studies and a wide range of practical applications in various fields. The ability to confidently work with fractions and whole numbers forms a cornerstone of mathematical literacy, enabling you to solve a diverse array of problems encountered in daily life, work, and academic pursuits. By mastering this seemingly simple calculation, you're building a strong foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
Division Using An Array
Sep 14, 2025
-
47 Days In Weeks
Sep 14, 2025
-
6 3 Kg To Pounds
Sep 14, 2025
-
Define Fee Simple Absolute
Sep 14, 2025
-
15 Percent Of 25
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 5 6 X 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.