52 Divided By 6
renascent
Sep 14, 2025 · 5 min read
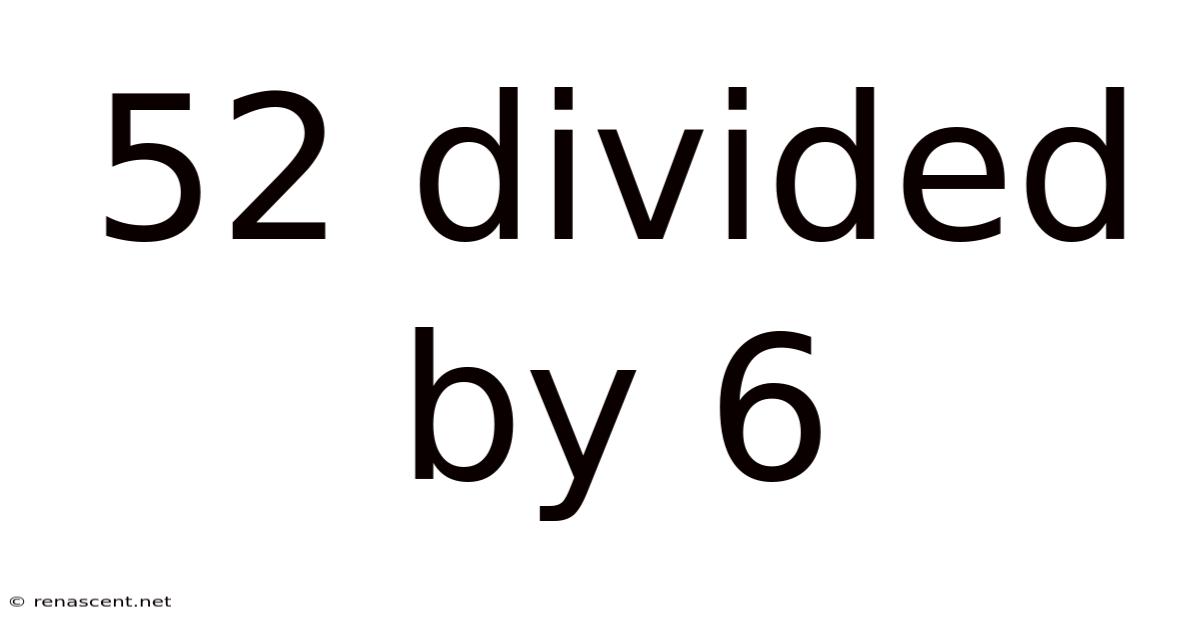
Table of Contents
Unveiling the Mystery: A Deep Dive into 52 Divided by 6
Introduction:
Dividing 52 by 6 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation offers a rich opportunity to explore several key mathematical concepts, from basic division to the nuances of remainders, fractions, and decimal representation. This comprehensive guide will delve into the different ways to solve 52 divided by 6, explaining the process step-by-step and exploring the deeper meaning behind the result. We’ll also address common questions and misconceptions surrounding this type of division problem. Understanding this seemingly simple calculation provides a strong foundation for more complex mathematical operations.
Understanding the Division Process: 52 ÷ 6
The core concept of division is about fair sharing. When we divide 52 by 6, we're asking: "If we have 52 items and want to divide them equally among 6 groups, how many items will be in each group?"
Long Division Method:
The most common method for solving this is long division. Here's how it works:
-
Set up the problem: Write 52 inside the division bracket (the dividend) and 6 outside (the divisor).
6 | 52 -
Divide the tens digit: How many times does 6 go into 5? It doesn't go at all, so we move to the next digit.
-
Combine tens and ones: Consider 52 as a whole. How many times does 6 go into 52? We can estimate this. 6 x 8 = 48 and 6 x 9 = 54. Since 54 is greater than 52, 8 is the closest whole number.
-
Multiply and subtract: Write the 8 above the 2 (the quotient). Multiply 6 by 8 (which is 48) and write this below 52. Subtract 48 from 52.
8 6 | 52 48 -- 4 -
The remainder: The result of the subtraction (4) is the remainder. This means that after dividing 52 into 6 equal groups, we have 4 items left over.
Therefore, 52 divided by 6 is 8 with a remainder of 4. We can write this as 8 R 4.
Representing the Result: Fractions and Decimals
While the whole number remainder is useful, representing the division using fractions or decimals provides a more complete picture.
Fractional Representation:
The remainder (4) represents the leftover portion. We can express this leftover portion as a fraction. The remainder becomes the numerator, and the divisor (6) becomes the denominator. So, the fractional representation of the remainder is 4/6. This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2. This simplifies to 2/3.
Therefore, 52 divided by 6 can also be expressed as 8 2/3. This mixed number indicates 8 whole groups and an additional 2/3 of a group.
Decimal Representation:
To express the result as a decimal, we can extend the long division process. After obtaining the remainder of 4, add a decimal point and a zero to the dividend (52). This allows us to continue the division.
8.666...
6 | 52.000
48
--
40
36
--
40
36
--
40
...
As you can see, the division continues indefinitely, resulting in a repeating decimal: 8.666... This can be represented as 8.6̅6̅. The bar above the 6 indicates that the digit 6 repeats infinitely.
Exploring the Concept of Remainders
The remainder in a division problem represents the amount left over after the division is complete. It's a crucial element because it highlights that the division isn't always perfectly even. Understanding remainders is fundamental in many real-world applications.
For instance, if you're dividing 52 candies among 6 friends, each friend gets 8 candies, and you have 4 candies left. The remainder (4) represents the candies that cannot be distributed equally. In this context, you might decide to share the remaining candies, or perhaps keep them for yourself.
Applications of Division with Remainders
Understanding how to perform and interpret division with remainders has numerous applications across various fields:
- Everyday life: Sharing items, calculating costs per unit, measuring quantities, etc.
- Computer science: Remainders are used in algorithms, hashing, and other computational processes.
- Engineering: Calculations involving material measurements and resource allocation often involve remainders.
- Data analysis: Analyzing datasets and identifying patterns frequently necessitates division and working with remainders.
Frequently Asked Questions (FAQ)
Q: Why is the decimal representation of 52/6 a repeating decimal?
A: The decimal representation is a repeating decimal because the division process never results in a zero remainder. The remainder 4 keeps reappearing, leading to the repeating sequence of 6s. This happens whenever the fraction involved (in this case, 2/3) cannot be expressed as a terminating decimal.
Q: What's the difference between a remainder and a fraction?
A: A remainder is the leftover amount after a division operation involving whole numbers. A fraction represents a part of a whole and can be used to express the remainder more precisely as a portion of the divisor. The remainder and fraction provide two ways of representing the same leftover amount.
Q: Can we use a calculator to solve this problem?
A: Yes, calculators can perform division. However, a calculator will typically provide the decimal representation (8.666...) rather than the whole number remainder (8 R 4) or the mixed number (8 2/3). Understanding the manual method is important for grasping the underlying mathematical principles.
Q: Are there other ways to solve 52 divided by 6?
A: While long division is the most common method, other approaches exist, particularly for smaller numbers. For example, you could use repeated subtraction, repeatedly subtracting 6 from 52 until you reach a number less than 6. The number of times you subtract 6 is the quotient, and the remaining number is the remainder.
Conclusion: Beyond the Numbers
The seemingly simple problem of 52 divided by 6 offers a gateway to deeper mathematical understanding. From the fundamental concepts of division and remainders to the intricacies of fractions and decimal representations, this calculation serves as a powerful example of how even basic arithmetic can reveal rich mathematical insights. Mastering this concept builds a solid foundation for tackling more complex mathematical problems in the future. The ability to represent the result in different forms (whole number with remainder, mixed number, and decimal) demonstrates a versatile understanding of numerical representation. Beyond the arithmetic itself, understanding the context and application of remainders is crucial in solving real-world problems. By exploring this simple problem, we've uncovered a wealth of mathematical knowledge that extends far beyond the initial question.
Latest Posts
Latest Posts
-
10 12 In Percentage
Sep 14, 2025
-
68 Inches In Ft
Sep 14, 2025
-
60 5 Kg To Lbs
Sep 14, 2025
-
Take Care Approach Rsa
Sep 14, 2025
-
Chairs For The Disabled
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 52 Divided By 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.