6/30 As A Percentage
renascent
Sep 23, 2025 · 5 min read
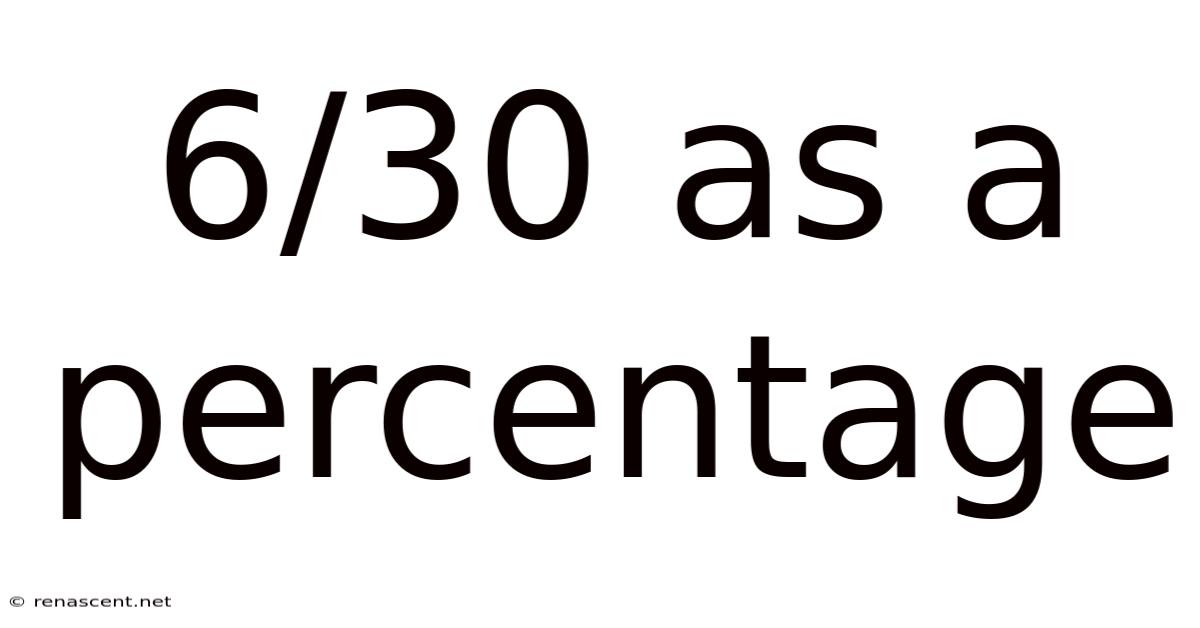
Table of Contents
Understanding 6/30 as a Percentage: A Comprehensive Guide
Many everyday situations require converting fractions to percentages. Understanding how to do this is a crucial skill, useful for everything from calculating discounts to understanding financial reports. This comprehensive guide will walk you through converting the fraction 6/30 to a percentage, explaining the process step-by-step and providing additional context to solidify your understanding of percentages and fractions. We'll explore the underlying mathematical principles and delve into practical applications. This article aims to make percentage calculations clear and easy, no matter your mathematical background.
Understanding Fractions and Percentages
Before diving into the conversion of 6/30, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, while the numerator indicates how many of those parts are being considered.
A percentage, on the other hand, is a way of expressing a fraction as a portion of 100. The word "percent" literally means "per hundred." So, 50% means 50 out of 100, or 50/100. Percentages are widely used because they provide a standardized and easily understandable way to compare different fractions.
Converting 6/30 to a Percentage: A Step-by-Step Guide
To convert the fraction 6/30 to a percentage, we need to follow these steps:
Step 1: Simplify the Fraction (If Possible)
The first step is to simplify the fraction 6/30 to its lowest terms. Both the numerator (6) and the denominator (30) are divisible by 6. Dividing both by 6, we get:
6 ÷ 6 = 1 30 ÷ 6 = 5
Therefore, the simplified fraction is 1/5. Simplifying the fraction makes the subsequent calculation easier.
Step 2: Convert the Simplified Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator by the denominator. In this case, we divide 1 by 5:
1 ÷ 5 = 0.2
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent sign (%).
0.2 x 100 = 20
Therefore, 0.2 is equivalent to 20%.
Conclusion of the Conversion:
Following these steps, we have successfully converted the fraction 6/30 to a percentage: 20%.
The Mathematical Explanation Behind the Conversion
The process of converting a fraction to a percentage is fundamentally about expressing the fraction as a proportion of 100. Let's break down the mathematics:
-
Fraction to Decimal: Dividing the numerator by the denominator gives us the decimal representation of the fraction. This represents the fraction as a part of one whole unit (1).
-
Decimal to Percentage: Multiplying the decimal by 100 scales the decimal to represent a part of 100. The result is the percentage equivalent.
Practical Applications of Percentage Calculations
Understanding how to convert fractions to percentages is a valuable skill with numerous real-world applications:
-
Financial Calculations: Calculating interest rates, discounts, tax rates, profit margins, and investment returns all involve working with percentages. For example, a 20% discount on a $100 item would save you $20 (20% of $100).
-
Data Analysis: Percentages are frequently used to represent data in charts and graphs, making it easier to visualize and interpret trends. For instance, comparing the percentage of students who passed a test across different years allows for easy comparison.
-
Statistics and Probability: Percentages are fundamental in statistics and probability. For example, expressing the probability of an event occurring as a percentage makes it more intuitive to understand.
-
Everyday Life: We encounter percentages in many everyday situations, such as calculating tips in restaurants, determining sale prices in stores, or understanding nutritional information on food labels.
Beyond 6/30: Converting Other Fractions to Percentages
The method outlined above can be applied to convert any fraction to a percentage. Here are a few examples:
-
3/4: 3 ÷ 4 = 0.75; 0.75 x 100 = 75%
-
2/5: 2 ÷ 5 = 0.4; 0.4 x 100 = 40%
-
1/2: 1 ÷ 2 = 0.5; 0.5 x 100 = 50%
-
12/25: 12 ÷ 25 = 0.48; 0.48 x 100 = 48%
Frequently Asked Questions (FAQ)
Q1: Why is simplifying the fraction important before converting to a percentage?
A1: Simplifying the fraction makes the calculations easier. Working with smaller numbers reduces the chance of errors and makes the process more efficient.
Q2: Can I convert a fraction to a percentage without simplifying it first?
A2: Yes, you can. However, the calculation will be more complex and might lead to more errors. Simplifying first is always recommended.
Q3: What if the fraction results in a repeating decimal?
A3: Some fractions, when converted to decimals, result in repeating decimals (e.g., 1/3 = 0.333...). In these cases, you can round the decimal to a certain number of decimal places before converting to a percentage. For example, you might round 0.333... to 0.33 and then convert it to 33%. However, always specify if you have rounded the number.
Q4: How do I convert a percentage back to a fraction?
A4: To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 75% becomes 75/100, which simplifies to 3/4.
Q5: Are there online calculators for converting fractions to percentages?
A5: Yes, many online calculators are available that can perform this conversion quickly and easily. However, understanding the underlying process is crucial for applying this skill effectively in various contexts.
Conclusion
Converting a fraction like 6/30 to a percentage involves a straightforward three-step process: simplifying the fraction, converting the simplified fraction to a decimal, and finally, multiplying the decimal by 100 to obtain the percentage. This skill is invaluable in a wide range of applications, from everyday financial transactions to complex data analysis. By understanding the underlying principles and practicing the steps, you can confidently navigate percentage calculations in your personal and professional life. Remember, the ability to convert fractions to percentages is a fundamental skill with broad applicability and empowers you to understand and interpret numerical data more effectively. Mastering this skill opens doors to a deeper understanding of the world around you, filled with numbers and data expressed in percentages.
Latest Posts
Latest Posts
-
1 36 In Percentage
Sep 23, 2025
-
24 30 As A Percentage
Sep 23, 2025
-
2 10 5 10
Sep 23, 2025
-
420 Minutes To Hours
Sep 23, 2025
-
1 5 Quarts To Litres
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 6/30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.