6 8 1 2
renascent
Sep 16, 2025 · 5 min read
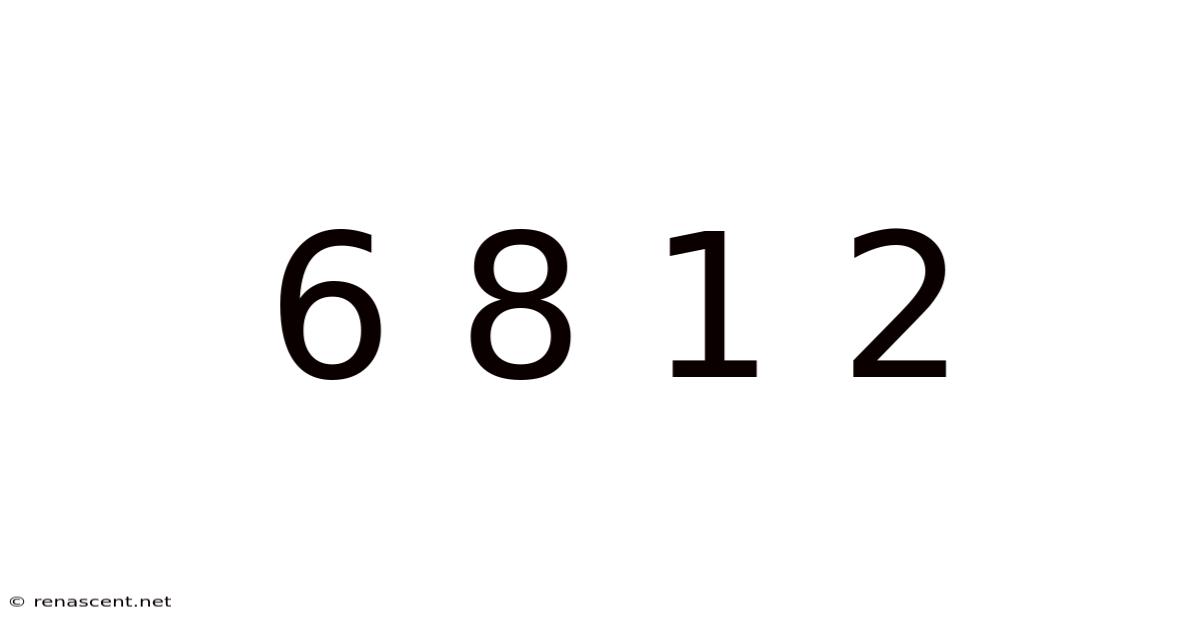
Table of Contents
Decoding the Mysterious Sequence: 6 8 1 2 – A Journey into Number Patterns and Problem Solving
The seemingly simple sequence 6, 8, 1, 2 might appear random at first glance. However, hidden within this short string of numbers lies a fascinating puzzle that invites us to explore various mathematical concepts and problem-solving strategies. This article delves deep into the potential interpretations of this sequence, examining different patterns, exploring mathematical principles, and ultimately demonstrating the beauty and complexity inherent in seemingly simple numerical puzzles. We'll uncover the hidden logic, discuss various possible solutions, and even touch upon the broader implications of pattern recognition in mathematics and beyond.
Potential Interpretations and Patterns
Before jumping to conclusions, it's crucial to acknowledge that without further context, multiple interpretations of the sequence 6, 8, 1, 2 are plausible. The lack of a clear pattern initially suggests that we need to consider different perspectives and mathematical operations to decipher its meaning. Let's explore several possibilities:
1. Modular Arithmetic and Cyclical Patterns:
One approach involves examining the sequence through the lens of modular arithmetic. Perhaps the numbers represent remainders after division by a specific number. Let's try a few common divisors:
- Modulo 7: If we consider the sequence modulo 7 (i.e., the remainder after dividing each number by 7), we get 6, 1, 1, 2. This doesn't immediately reveal a clear pattern.
- Modulo 9: Modulo 9 yields 6, 8, 1, 2. Again, no readily apparent pattern emerges.
- Modulo 10: This gives 6, 8, 1, 2, which is identical to the original sequence. This doesn't help us find a pattern either.
While modular arithmetic doesn't yield an obvious solution in this instance, it illustrates a valuable problem-solving technique for analyzing numerical sequences. Exploring different moduli helps us explore potential cyclical or repeating patterns within the data.
2. Differences and Sequences of Differences:
Another common strategy in analyzing numerical sequences is to examine the differences between consecutive terms. Let's calculate the differences between adjacent numbers in our sequence:
- 8 - 6 = 2
- 1 - 8 = -7
- 2 - 1 = 1
The differences themselves (2, -7, 1) don't immediately reveal a pattern either. We could even calculate the second differences (the differences between the first differences):
- -7 - 2 = -9
- 1 - (-7) = 8
The second differences (-9, 8) also don't show an easily discernible pattern. However, this method highlights another important analytical approach: looking for underlying patterns within the differences themselves.
3. Mathematical Operations and Transformations:
It's possible that the sequence is generated by a specific mathematical operation or transformation. Let's explore a few possibilities:
- Addition/Subtraction: No simple addition or subtraction rule appears to generate the sequence.
- Multiplication/Division: Similarly, no obvious multiplication or division rule creates this sequence.
- More Complex Operations: More complex operations involving combinations of addition, subtraction, multiplication, division, or even exponents might be needed, but without further information or context, identifying such an operation is challenging.
4. External Factors and Contextual Clues:
The lack of a clear inherent pattern within the numbers themselves suggests that the sequence might rely on external factors or contextual clues. For instance:
- Coding or Encryption: The sequence might be part of a code or encryption scheme. Further information about the context in which this sequence appeared would be essential to decode it.
- Base Conversion: The numbers might represent a value in a different number system (e.g., base-16, binary). Without additional details, this is pure speculation.
- Coordinate System: The numbers could represent coordinates in a two-dimensional or higher-dimensional space. However, this would require further information.
Expanding the Possibilities: Exploring Problem-Solving Strategies
The challenge presented by the sequence 6, 8, 1, 2 underscores the importance of robust problem-solving strategies when confronted with seemingly ambiguous numerical patterns. These strategies extend far beyond simple mathematical operations and include:
- Systematic Exploration: Testing different mathematical approaches (as we did with modular arithmetic and differences) is crucial.
- Pattern Recognition: Developing a keen eye for identifying subtle patterns or repeating sequences is vital.
- Trial and Error: Experimentation is key. Trying different approaches without being discouraged by initial failures is essential.
- Creative Thinking: Stepping outside the box and considering non-traditional interpretations is often necessary.
- Contextual Awareness: Understanding the origin or context of the sequence (if available) can drastically alter the approach.
The Importance of Context in Pattern Recognition
The ambiguity surrounding the sequence 6, 8, 1, 2 highlights a key aspect of pattern recognition: the crucial role of context. Without additional information regarding the source or purpose of the sequence, our ability to decipher its meaning is significantly limited. In real-world applications of pattern recognition, such as data analysis, machine learning, and cryptography, understanding the context is often paramount for accurate interpretation and successful problem-solving.
Conclusion: Embracing the Mystery and Continuing the Search
While we haven't definitively cracked the code of the sequence 6, 8, 1, 2, our exploration has highlighted several valuable problem-solving techniques and emphasized the importance of context in interpreting numerical patterns. The sequence itself serves as a powerful reminder that even seemingly simple puzzles can conceal significant depth and complexity. Its ambiguity encourages creative thinking and reinforces the iterative nature of mathematical problem-solving – a process of exploration, experimentation, and perseverance. The journey of deciphering this sequence, while inconclusive in this instance, provides a valuable framework for tackling more intricate numerical puzzles in the future. Perhaps with additional information or a different perspective, the true meaning of 6, 8, 1, 2 might one day be revealed.
The challenge remains open. This exploration serves not only as a solution attempt but also as a pedagogical tool, showcasing the various methods employed in deciphering numerical sequences and underscoring the importance of critical thinking and creative problem-solving in mathematics and beyond. The seemingly simple can often harbor unexpected complexity, and the pursuit of understanding these complexities is what drives mathematical exploration.
Latest Posts
Latest Posts
-
23 7 Kg To Pounds
Sep 16, 2025
-
Sample Of Narrative Poetry
Sep 16, 2025
-
23 Kj To Calories
Sep 16, 2025
-
220 Calories To Kilojoules
Sep 16, 2025
-
18 And 30 Hcf
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 6 8 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.