7 Divided By 10
renascent
Sep 21, 2025 · 6 min read
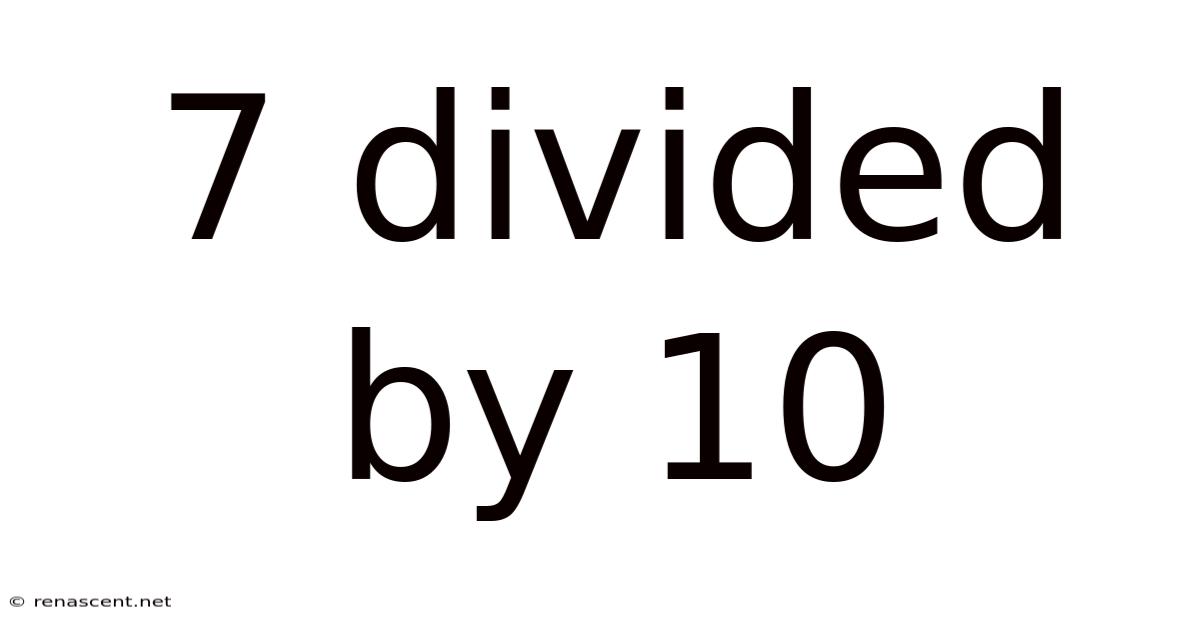
Table of Contents
Unveiling the Mystery: A Deep Dive into 7 Divided by 10
This article explores the seemingly simple calculation of 7 divided by 10, delving far beyond the basic answer. We will unpack the various ways to represent this division, examine its practical applications, and explore the underlying mathematical concepts. Understanding this seemingly trivial problem unlocks a deeper appreciation for fractions, decimals, percentages, and their interconnectedness within the broader field of mathematics. This comprehensive guide is designed for learners of all levels, from elementary school students grasping the basics of division to those seeking a more nuanced understanding of mathematical representations.
Understanding Division: The Fundamentals
Before diving into 7 divided by 10, let's refresh our understanding of division itself. Division is essentially the process of splitting a quantity into equal parts. In the expression 7 ÷ 10 (or 7/10), we're asking: "If we divide 7 into 10 equal parts, how large is each part?"
This differs from the more intuitive concept of splitting a whole number into a smaller number of parts. For example, dividing 10 by 2 is straightforward: each part is 5. However, when the dividend (7 in our case) is smaller than the divisor (10), we enter the realm of fractions and decimals.
Calculating 7 Divided by 10: Methods and Representations
There are several ways to calculate and represent the result of 7 divided by 10:
-
Fraction: The most direct representation is the fraction 7/10. This clearly shows that we have 7 parts out of a possible 10. Fractions are fundamental in mathematics and provide a clear, concise way to express parts of a whole.
-
Decimal: To express 7/10 as a decimal, we perform the division: 7 ÷ 10 = 0.7. This decimal representation is readily understood and widely used in various applications.
-
Percentage: A percentage represents a fraction out of 100. To convert 7/10 to a percentage, we multiply by 100%: (7/10) * 100% = 70%. This representation is particularly useful when comparing proportions or expressing probabilities.
These three representations – fraction, decimal, and percentage – are all equivalent and interchangeable, offering different perspectives on the same value. Choosing the most appropriate representation often depends on the context of the problem.
Real-World Applications of 7/10
The seemingly simple calculation of 7 divided by 10 has numerous applications in real-world scenarios:
-
Proportions and Ratios: If you have a bag of 10 marbles, and 7 are red, then the proportion of red marbles is 7/10, or 70%.
-
Measurements: Imagine measuring 7 centimeters out of a total length of 10 centimeters. This would be represented as 7/10 or 0.7 of the total length.
-
Discounts and Sales: A 70% discount means you're paying only 30% (100% - 70%) of the original price. This is directly related to the fraction 7/10.
-
Probability: If there's a 70% chance of rain, this signifies a probability of 7/10.
-
Data Representation: In data analysis and statistics, 7/10 might represent a proportion of a specific group within a larger population.
These examples highlight the practical relevance of understanding this calculation and its various representations.
Exploring the Mathematical Concepts
Understanding 7 divided by 10 allows us to explore several key mathematical concepts:
-
Fractions as Ratios: The fraction 7/10 represents a ratio of 7 to 10. This concept extends to a wide range of applications, from comparing quantities to understanding scales and proportions.
-
Decimal Representation: Converting a fraction to a decimal helps us visualize the value more readily, particularly in situations involving calculations or comparisons with other decimal numbers.
-
Percentage as Proportion: The percentage representation (70%) offers a convenient way to express parts of a whole in relation to 100, facilitating comparisons and interpretations.
-
Equivalence: The equivalence of 7/10, 0.7, and 70% highlights the interconnectedness of different mathematical representations, emphasizing that they all denote the same value.
-
Division with Remainders: While 7 divided by 10 doesn't result in a remainder in the decimal or fraction form, understanding the concept of remainders is crucial for more complex division problems involving whole numbers.
Further Exploration: Expanding the Concept
The principles applied to 7 divided by 10 can be extended to more complex division problems. Consider these examples:
-
Dividing larger numbers by 10: Dividing any number by 10 simply involves moving the decimal point one place to the left. For instance, 77 divided by 10 is 7.7.
-
Dividing by other multiples of 10: Dividing by 100, 1000, and so on follows a similar pattern: moving the decimal point to the left by the number of zeros.
-
Dividing fractions: Dividing fractions involves inverting the second fraction and multiplying. For instance, (7/10) ÷ (1/2) = (7/10) * (2/1) = 14/10 = 7/5 = 1.4
-
Mixed numbers and decimals: Handling more complex division problems often involves combining techniques for dealing with mixed numbers (a whole number and a fraction), decimals, and percentages.
Frequently Asked Questions (FAQ)
-
Q: Why is 7 divided by 10 less than 1?
- A: Because the dividend (7) is smaller than the divisor (10). When the dividend is smaller than the divisor, the result is always a proper fraction or a decimal less than 1.
-
Q: Can 7/10 be simplified further?
- A: No, 7 and 10 share no common factors other than 1, making 7/10 its simplest form.
-
Q: What is the reciprocal of 7/10?
- A: The reciprocal is found by inverting the fraction, resulting in 10/7.
-
Q: How do I convert 7/10 to a percentage without multiplying by 100%?
- A: You can understand it conceptually: 7/10 means 7 out of every 10, so to find how many out of 100, you can set up a proportion: 7/10 = x/100. Solving for x gives you 70.
-
Q: What are some real-world examples beyond the ones mentioned?
- A: Think about cooking recipes (7 out of 10 cups of flour), scoring on a test (7 out of 10 questions correct), or even dividing a group of people into smaller teams.
Conclusion: Beyond the Basic Calculation
While the calculation of 7 divided by 10 might seem trivial at first glance, a closer examination reveals a wealth of mathematical concepts and practical applications. Understanding the different representations – fraction, decimal, and percentage – and their interrelationships is crucial for navigating various mathematical and real-world problems. This exploration goes beyond simply finding the answer (0.7 or 7/10 or 70%) and deepens our understanding of fundamental mathematical principles, showcasing the interconnectedness of seemingly simple calculations with broader mathematical concepts and real-world scenarios. This comprehensive understanding is essential for building a solid foundation in mathematics and its practical applications.
Latest Posts
Latest Posts
-
B And D Plumbing
Sep 21, 2025
-
Quotes About John Proctor
Sep 21, 2025
-
4 Of 100 000
Sep 21, 2025
-
4 X 5 3
Sep 21, 2025
-
19 24 X 100
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 7 Divided By 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.