7 Divided By 23
renascent
Sep 18, 2025 · 6 min read
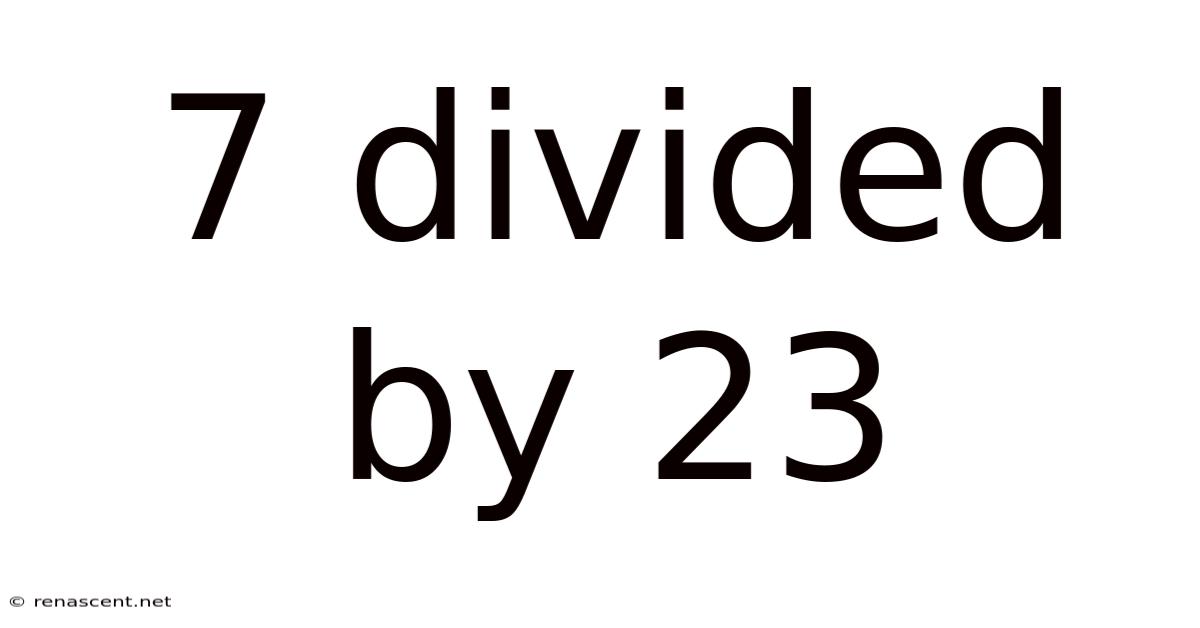
Table of Contents
Unveiling the Mystery: A Deep Dive into 7 Divided by 23
Understanding division, especially when dealing with numbers that don't divide evenly, can feel daunting. This article delves into the seemingly simple calculation of 7 divided by 23, exploring not just the answer but the underlying mathematical concepts, practical applications, and different ways to approach this problem. We'll unravel the complexities, providing a comprehensive guide accessible to everyone, regardless of their mathematical background. This detailed explanation will cover the core concepts of division, various methods of calculation, and potential real-world applications, making this a valuable resource for students, educators, and anyone curious about the intricacies of arithmetic.
Understanding Division: The Basics
Before we tackle 7 divided by 23, let's refresh our understanding of division. Division is essentially the process of splitting a quantity into equal parts. In the expression "a divided by b," denoted as a ÷ b or a/b, 'a' is the dividend (the number being divided), and 'b' is the divisor (the number by which we are dividing). The result is called the quotient.
When the dividend is perfectly divisible by the divisor (meaning there's no remainder), the result is a whole number. However, in many cases, such as 7 divided by 23, the division results in a fraction or decimal. This occurs when the dividend is smaller than the divisor, or when the dividend is not a multiple of the divisor.
Calculating 7 Divided by 23: Methods and Approaches
There are several ways to calculate 7 divided by 23:
1. Long Division:
This is a classic method for performing division manually. While it might seem tedious for a simple problem like this, it's crucial to understand the process for more complex divisions.
- Set up the long division problem: 23 | 7
- Since 7 is smaller than 23, we add a decimal point to the quotient (0.) and a zero to the dividend (70).
- Now, we ask how many times 23 goes into 70. It goes in 2 times (23 x 2 = 46).
- Subtract 46 from 70, leaving 24.
- Add another zero to the remainder (240).
- How many times does 23 go into 240? It goes in 10 times (23 x 10 = 230).
- Subtract 230 from 240, leaving 10.
- Continue this process adding zeros and repeating the steps to reach the desired level of accuracy.
The process continues indefinitely, generating a non-terminating, repeating decimal. We can approximate the answer to a certain number of decimal places. Using long division, we find that 7 divided by 23 is approximately 0.3043478...
2. Using a Calculator:
The simplest way to calculate 7 divided by 23 is by using a calculator. Simply input "7 ÷ 23" or "7/23" and the calculator will provide the decimal approximation.
3. Converting to a Fraction:
The result of 7 divided by 23 can also be expressed as a fraction: 7/23. This fraction is already in its simplest form, as 7 and 23 share no common factors other than 1.
Understanding the Decimal Result: Repeating Decimals
The result of 7 divided by 23 is a repeating decimal. This means that the decimal portion doesn't terminate but instead repeats a sequence of digits indefinitely. The repeating sequence in this case is relatively long, making it impractical to write out the entire repeating sequence. We usually represent repeating decimals using a bar over the repeating sequence. However, because the repeating sequence in this case is lengthy, it's easier to use an approximation.
Practical Applications: Real-World Examples
While dividing 7 by 23 might seem abstract, similar calculations arise in various real-world situations:
-
Proportion and Ratio: Imagine you have 7 liters of paint and need to divide it equally among 23 surfaces. The calculation 7/23 would determine the amount of paint each surface receives.
-
Probability: If you have 7 favorable outcomes out of a total of 23 possible outcomes, the probability of the favorable event is 7/23.
-
Unit Conversion: While less directly applicable, the principles of division are fundamental to unit conversion problems, where you might need to divide a quantity by a conversion factor.
-
Finance: Dividing your total earnings over a period of 23 weeks (or days/months) by 23 helps to calculate your weekly/daily/monthly income.
-
Resource Allocation: This type of division is crucial for resource management where a limited resource must be distributed among multiple entities.
These examples showcase that the concept, even with seemingly insignificant numbers, underlies practical calculations across diverse fields.
Beyond the Calculation: Exploring Further Concepts
This seemingly simple division problem opens doors to exploring deeper mathematical concepts:
-
Rational Numbers: The result 7/23 is a rational number – a number that can be expressed as a fraction of two integers.
-
Irrational Numbers: In contrast, numbers like π (pi) and √2 (the square root of 2) are irrational numbers – they cannot be expressed as a fraction of two integers and their decimal representations neither terminate nor repeat.
-
Real Numbers: Both rational and irrational numbers together form the set of real numbers.
Understanding these distinctions provides a broader perspective on the nature of numbers and their properties.
Frequently Asked Questions (FAQ)
Q: Is there a way to simplify 7/23 further?
A: No, 7 and 23 are both prime numbers, meaning they are only divisible by 1 and themselves. Therefore, the fraction 7/23 is already in its simplest form.
Q: Why does 7/23 result in a repeating decimal?
A: A fraction results in a repeating decimal when the denominator (in this case, 23) contains prime factors other than 2 and 5. Since 23 is a prime number other than 2 and 5, the decimal representation will repeat.
Q: How accurate does the decimal approximation need to be?
A: The required accuracy depends on the context. For many practical applications, a few decimal places (e.g., 0.304) might be sufficient. However, for highly precise calculations, you may need more decimal places.
Q: Can I use a different method to calculate 7 divided by 23?
A: While long division and calculators are the most common methods, there are other approaches, including using computer programming languages or specialized mathematical software that provide high-precision calculations and can manage repeating decimals effectively.
Conclusion: The Significance of a Simple Calculation
While seemingly trivial, the calculation of 7 divided by 23 provides a valuable opportunity to explore fundamental mathematical concepts. From understanding long division to grasping the nature of repeating decimals and the broader classification of numbers, this simple problem serves as a gateway to a deeper appreciation of arithmetic and its applications in the real world. Remember, even the simplest calculations can reveal profound mathematical insights when examined closely. The seemingly insignificant 7 divided by 23 exemplifies the beauty and complexity hidden within the seemingly simple. By understanding the process and the underlying principles, we build a stronger foundation for tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
Swallowed A Fly Lyrics
Sep 18, 2025
-
30 Out Of 42
Sep 18, 2025
-
105 9 Kg In Stone
Sep 18, 2025
-
Grains To Grams Calculator
Sep 18, 2025
-
7 9 In Decimal Form
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 7 Divided By 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.