72 Divided By 4
renascent
Sep 15, 2025 · 6 min read
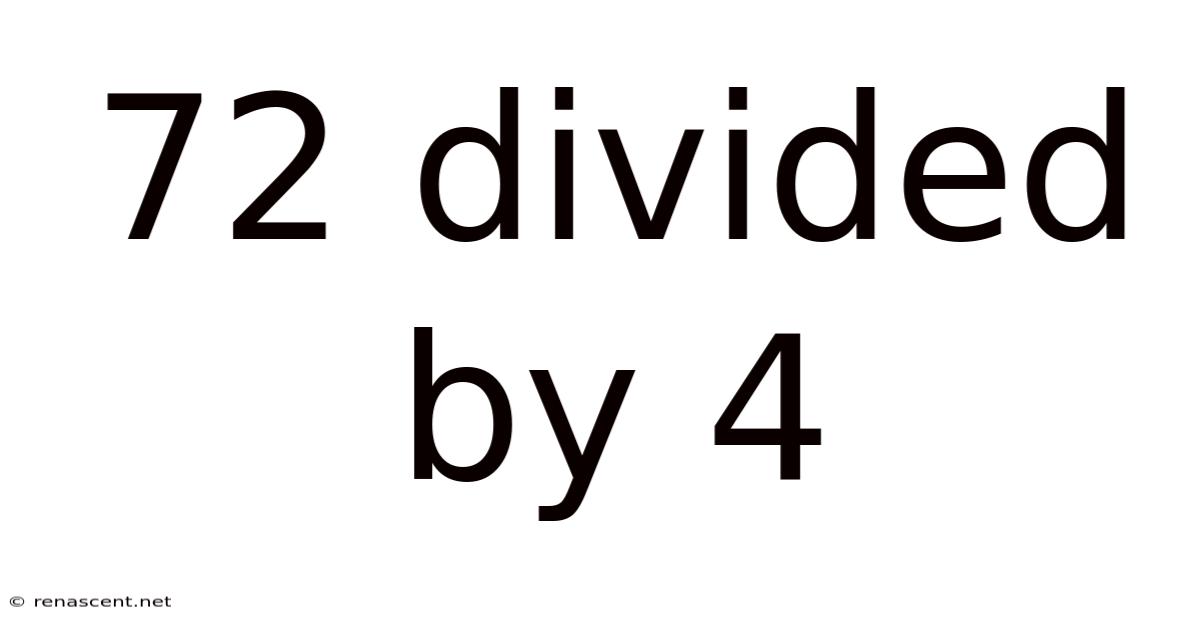
Table of Contents
Unpacking 72 Divided by 4: A Deep Dive into Division
This article explores the seemingly simple calculation of 72 divided by 4 (72 ÷ 4), delving far beyond the basic answer to uncover the underlying mathematical principles, different methods of solving the problem, and real-world applications. Understanding division at this level builds a strong foundation for more complex mathematical concepts. We'll cover various approaches, from basic arithmetic to more advanced strategies, making this a valuable resource for students and anyone seeking a deeper understanding of division.
Introduction: The Fundamentals of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts. In the equation 72 ÷ 4, we're asking: "How many times does 4 fit into 72?" The answer, as we'll see in multiple ways, is 18. But this simple answer belies a wealth of mathematical understanding. This exploration will cover various methods for solving this problem, highlighting the interconnectedness of mathematical concepts.
Method 1: Repeated Subtraction
The most fundamental approach to division is repeated subtraction. Imagine you have 72 apples, and you want to divide them equally among 4 friends. You can repeatedly subtract 4 apples until you have none left. Let's do it:
- 72 - 4 = 68
- 68 - 4 = 64
- 64 - 4 = 60
- 60 - 4 = 56
- 56 - 4 = 52
- 52 - 4 = 48
- 48 - 4 = 44
- 44 - 4 = 40
- 40 - 4 = 36
- 36 - 4 = 32
- 32 - 4 = 28
- 28 - 4 = 24
- 24 - 4 = 20
- 20 - 4 = 16
- 16 - 4 = 12
- 12 - 4 = 8
- 8 - 4 = 4
- 4 - 4 = 0
We subtracted 4 eighteen times before reaching 0. Therefore, 72 ÷ 4 = 18. This method demonstrates the core concept of division as repeated subtraction, making it intuitively clear, especially for younger learners.
Method 2: Long Division
Long division is a more formal and efficient method for larger numbers. Let's apply it to 72 ÷ 4:
18
4 | 72
-4
32
-32
0
- We start by dividing 4 into the first digit of 72, which is 7. 4 goes into 7 once (4 x 1 = 4), so we write a 1 above the 7.
- We subtract 4 from 7, leaving 3.
- We bring down the next digit, 2, making it 32.
- We divide 4 into 32. 4 goes into 32 eight times (4 x 8 = 32), so we write an 8 above the 2.
- We subtract 32 from 32, leaving 0.
The result, 18, is placed at the top. This method is systematic and useful for larger and more complex division problems.
Method 3: Multiplication as the Inverse
Division and multiplication are inverse operations. This means that if we know the result of a division problem, we can check our answer by multiplying the quotient by the divisor. In this case:
18 x 4 = 72
Since the product equals the original dividend (72), we've confirmed that our answer (18) is correct. This method is crucial for verifying the accuracy of division calculations.
Method 4: Factoring and Simplification
We can also approach this problem using prime factorization. Both 72 and 4 can be broken down into their prime factors:
- 72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
- 4 = 2 x 2 = 2²
Now, we can rewrite the division problem as:
(2³ x 3²) ÷ 2²
Simplifying, we can cancel out two 2's from both the numerator and the denominator:
(2 x 3²) = 2 x 9 = 18
This method showcases the relationship between division and prime factorization, offering a deeper understanding of number composition.
Real-World Applications: Why is this Important?
Understanding division, even a seemingly simple problem like 72 ÷ 4, has numerous practical applications in everyday life:
- Sharing Equally: Dividing resources fairly among friends, family, or colleagues.
- Calculating Unit Costs: Determining the price per item when buying in bulk. If 72 pencils cost $4, each pencil costs $4 ÷ 72 = $0.055 or approximately 6 cents.
- Recipe Scaling: Adjusting recipe ingredients for different quantities.
- Averaging: Finding the average value of a set of numbers. For example, if four students scored a total of 72 points on a test, the average score would be 72 ÷ 4 = 18 points.
- Measurement Conversions: Converting units of measurement, like dividing inches into feet or centimeters into meters.
- Financial Calculations: Dividing expenses among multiple people or calculating interest rates.
Mathematical Concepts Beyond the Basics:
The simple calculation 72 ÷ 4 touches upon several important mathematical concepts:
- Divisibility Rules: The divisibility rule for 4 states that a number is divisible by 4 if its last two digits are divisible by 4. Since 72 is divisible by 4 (72/4 =18), we know that the entire number is also divisible by 4.
- Factors and Multiples: 4 is a factor of 72, meaning 4 divides 72 evenly. Conversely, 72 is a multiple of 4.
- Quotient and Remainder: In division problems, the result is called the quotient. In this case, the quotient is 18. A remainder occurs when a number doesn't divide evenly. In this case, there's no remainder.
- Integer Division: This calculation involves only integers (whole numbers) resulting in an integer quotient.
Frequently Asked Questions (FAQ)
- What if I get a remainder? If you were dividing a number that wasn't evenly divisible by 4, you would have a remainder. For example, 75 ÷ 4 would result in a quotient of 18 with a remainder of 3.
- Are there other ways to solve this problem? Yes, as detailed above, there are several different methods that can all lead to the same correct answer. The best method depends on your understanding of the underlying concepts and your personal preference.
- Why is understanding division important? Division is a fundamental building block for more advanced mathematical concepts, and its applications are widespread in everyday life. A strong grasp of division is crucial for success in mathematics and beyond.
- What if the numbers were much larger? For larger numbers, long division is the most efficient method. However, the underlying principles remain the same.
Conclusion: Mastering Division's Fundamentals
While seemingly simple, the calculation 72 ÷ 4 provides a gateway to a deeper understanding of division and its place within the broader world of mathematics. Through repeated subtraction, long division, multiplication as the inverse operation, and factorization, we’ve explored various paths to the solution, highlighting the interconnectedness of these mathematical concepts. This comprehensive exploration underscores the significance of mastering even seemingly basic arithmetic operations, as they form the foundation for more complex problem-solving and applications in numerous areas of life. Remember to practice these different methods to strengthen your understanding and confidence in tackling division problems of any size.
Latest Posts
Latest Posts
-
Km 2 To Km
Sep 15, 2025
-
350 Minutes To Hours
Sep 15, 2025
-
112 Days In Months
Sep 15, 2025
-
8lbs 4oz In Kg
Sep 15, 2025
-
56 Fahrenheit In Celsius
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 72 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.