78 Divided By 6
renascent
Sep 22, 2025 · 6 min read
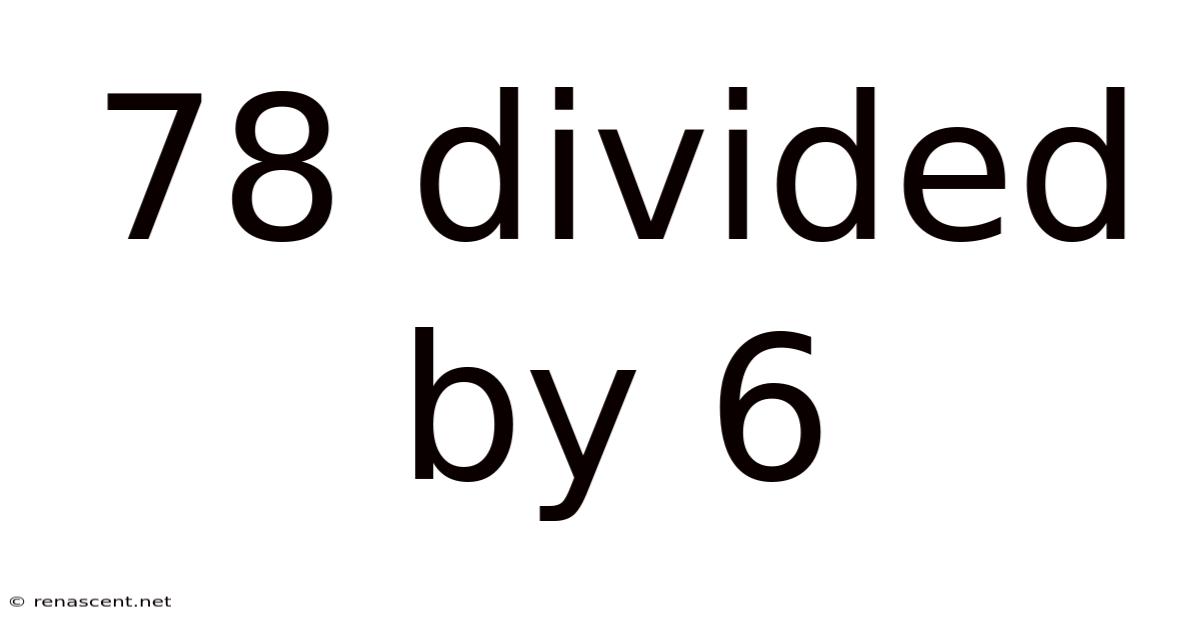
Table of Contents
Unveiling the Mystery: A Deep Dive into 78 Divided by 6
Introduction:
Dividing 78 by 6 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation offers a fantastic opportunity to explore several key mathematical concepts, delve into different solution methods, and appreciate the beauty of mathematical precision. This article will not only provide the answer to 78 ÷ 6 but also explain the process in detail, explore alternative approaches, and discuss the underlying principles. We'll even touch upon real-world applications and address frequently asked questions, making this a comprehensive guide for anyone curious about this seemingly simple division problem. This exploration will cover long division, understanding remainders, and even visualizing the division process.
Understanding Division:
Before we tackle 78 ÷ 6, let's briefly review the fundamental concept of division. Division is essentially the inverse operation of multiplication. While multiplication combines equal groups to find a total, division breaks a total into equal groups to find the size or number of those groups. In the context of 78 ÷ 6, we're asking: "How many times does 6 fit into 78?" or "If we divide 78 into 6 equal groups, how many will be in each group?"
Method 1: Long Division
Long division is a standard algorithm used to solve division problems, especially those involving larger numbers. Here's how to solve 78 ÷ 6 using long division:
-
Set up the problem: Write the dividend (78) inside the long division symbol (÷) and the divisor (6) outside.
6 | 78 -
Divide the tens digit: How many times does 6 go into 7? It goes in once (6 x 1 = 6). Write the 1 above the 7.
1 6 | 78 -
Subtract: Subtract the product (6) from the tens digit (7).
1 6 | 78 -6 --- 1 -
Bring down the ones digit: Bring down the ones digit (8) next to the remainder (1).
1 6 | 78 -6 --- 18 -
Divide the new number: How many times does 6 go into 18? It goes in three times (6 x 3 = 18). Write the 3 above the 8.
13 6 | 78 -6 --- 18 -
Subtract again: Subtract the product (18) from the new number (18).
13 6 | 78 -6 --- 18 -18 --- 0 -
The quotient: The result (0) indicates there's no remainder. The quotient, which is the answer to the division problem, is 13.
Therefore, 78 ÷ 6 = 13.
Method 2: Repeated Subtraction
This method is a more intuitive approach, particularly helpful for visualizing the division process. We repeatedly subtract the divisor (6) from the dividend (78) until we reach 0 or a number smaller than the divisor. The number of times we subtract represents the quotient.
78 - 6 = 72 72 - 6 = 66 66 - 6 = 60 60 - 6 = 54 54 - 6 = 48 48 - 6 = 42 42 - 6 = 36 36 - 6 = 30 30 - 6 = 24 24 - 6 = 18 18 - 6 = 12 12 - 6 = 6 6 - 6 = 0
We subtracted 6 thirteen times, confirming that 78 ÷ 6 = 13.
Method 3: Using Multiplication Facts
This method relies on your knowledge of multiplication tables. You need to find the multiple of 6 that equals 78 or is closest to 78 without exceeding it. Since 6 x 13 = 78, we know that 78 ÷ 6 = 13. This method is efficient for those who have memorized their multiplication tables.
Understanding Remainders:
While 78 ÷ 6 results in a whole number (13), division problems don't always yield a clean quotient. Sometimes, there's a remainder – a number left over after the division. Let's consider an example: 79 ÷ 6.
Using long division:
13
6 | 79
-6
---
19
-18
---
1
Here, the quotient is 13, and the remainder is 1. This can be expressed as 13 R 1 (13 with a remainder of 1) or as a mixed number (13 1/6).
Real-World Applications:
Understanding division is crucial in various everyday situations. Consider these examples:
- Sharing equally: If you have 78 cookies to share equally among 6 friends, each friend receives 13 cookies.
- Grouping items: If you need to arrange 78 chairs into rows of 6, you'll have 13 rows.
- Calculating unit price: If 6 apples cost 78 cents, each apple costs 13 cents.
- Measurement conversions: Dividing helps convert larger units into smaller ones (e.g., converting minutes into seconds).
Mathematical Principles:
The division of 78 by 6 is governed by fundamental principles of arithmetic:
- Associative property of multiplication: This property allows you to group factors differently without changing the product. It isn't directly applied in this specific problem, but it underlies the various methods used to solve it.
- Distributive property: This property lets you distribute a factor across terms within parentheses, which is implicitly used when breaking down the division into steps.
- Inverse relationship between multiplication and division: This core principle is the foundation of the entire concept of division. Because 6 x 13 = 78, we know that 78 ÷ 6 = 13.
Visualizing the Division:
Imagine you have 78 identical objects. You want to arrange them into 6 equal groups. After arranging them, you'll find 13 objects in each group. This visual representation reinforces the concept of dividing a total into equal parts.
Frequently Asked Questions (FAQ):
- Q: What if I get a decimal answer when dividing 78 by 6? A: You shouldn't get a decimal answer when dividing 78 by 6. The answer is a whole number, 13. If you're getting a decimal, double-check your calculations.
- Q: Are there other ways to solve 78 ÷ 6? A: Yes, you can use a calculator or different division methods depending on your preference and the tools available to you. The methods discussed above are just a few examples.
- Q: What's the importance of understanding remainders in division? A: Understanding remainders is crucial for situations where items can't be divided perfectly into equal groups. The remainder represents the amount left over.
- Q: How can I improve my division skills? A: Consistent practice with various division problems, mastering multiplication tables, and understanding the different methods of division will enhance your skills.
Conclusion:
While the answer to 78 divided by 6 is simply 13, the journey to arrive at this answer has illuminated several fundamental mathematical concepts and problem-solving techniques. From long division and repeated subtraction to leveraging multiplication facts and visualizing the division process, we’ve explored multiple avenues to understand this seemingly basic calculation. This comprehensive approach not only provides the solution but also fosters a deeper understanding of division, its applications, and its underlying mathematical principles. The ability to solve problems like this efficiently and accurately is a building block for more advanced mathematical concepts, and appreciating the elegance of these seemingly simple calculations lays a strong foundation for future mathematical endeavors. Remember, the key to mastering math isn't just about getting the right answer but understanding why that answer is correct and how it relates to broader mathematical principles.
Latest Posts
Latest Posts
-
Lewis Diagram For H2o2
Sep 22, 2025
-
Ppt On Apple Inc
Sep 22, 2025
-
4 X 3 16
Sep 22, 2025
-
Alarm For 8 30 A M
Sep 22, 2025
-
45 Degrees In Fahrenheit
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 78 Divided By 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.