8/20 As A Percentage
renascent
Sep 24, 2025 · 5 min read
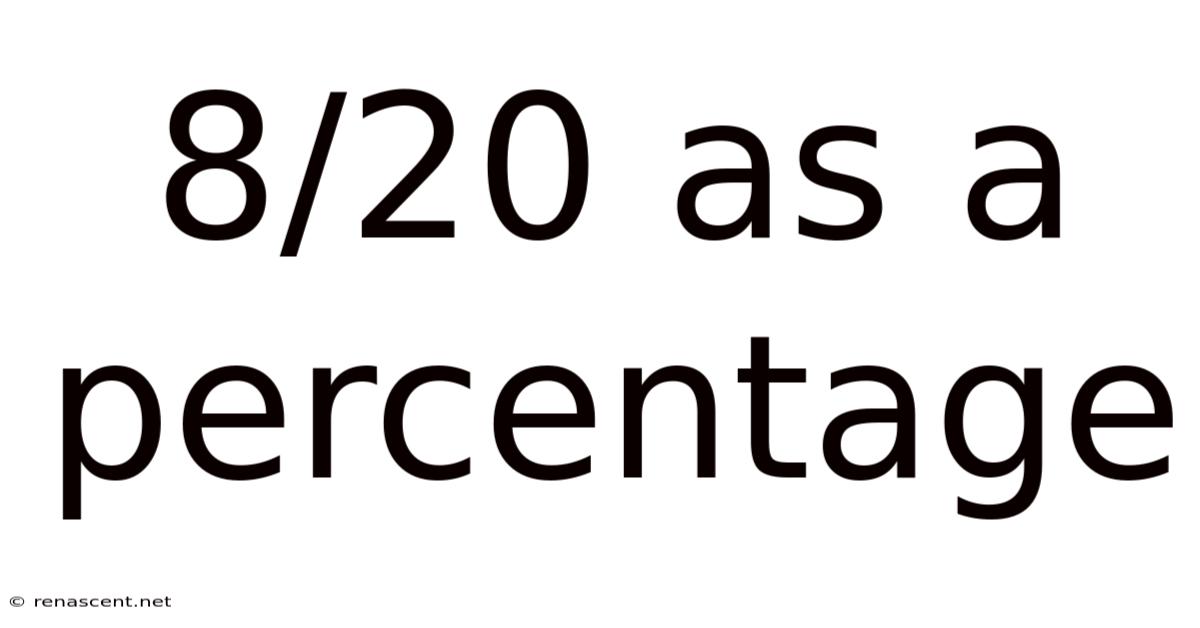
Table of Contents
8/20 as a Percentage: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and grades to analyzing data and understanding financial reports. This comprehensive guide will delve into the process of converting the fraction 8/20 into a percentage, explaining the underlying principles and providing practical examples to solidify your understanding. We'll explore various methods, address common misconceptions, and even tackle related percentage calculations to build a robust foundation in this important mathematical concept.
Introduction: Understanding Fractions and Percentages
Before diving into the conversion of 8/20, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of parts in the whole.
A percentage, on the other hand, is a way of expressing a fraction as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." Percentages are widely used because they provide a standardized way to compare different fractions and proportions.
Method 1: Simplifying the Fraction
The simplest way to convert 8/20 to a percentage is to first simplify the fraction. Notice that both the numerator (8) and the denominator (20) are divisible by 4. Simplifying the fraction gives us:
8 ÷ 4 / 20 ÷ 4 = 2/5
This simplified fraction, 2/5, represents the same proportion as 8/20. Now, we can easily convert this simplified fraction to a percentage.
Method 2: Direct Conversion using Division
To convert any fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100. Let's apply this method to 8/20:
8 ÷ 20 = 0.4
Now, multiply the decimal result by 100:
0.4 x 100 = 40%
Therefore, 8/20 is equal to 40%.
Method 3: Using Proportions
Another way to approach this problem is to use proportions. We can set up a proportion where x represents the percentage we're trying to find:
8/20 = x/100
To solve for x, we can cross-multiply:
20x = 800
Now, divide both sides by 20:
x = 40
So, x = 40%, confirming our previous results.
Explanation: Why 8/20 Equals 40%
The reason 8/20 equates to 40% lies in the fundamental definition of a percentage. A percentage expresses a fraction as a proportion of 100. When we simplify 8/20 to 2/5, we are essentially finding an equivalent fraction with a denominator of 5. To convert this to a fraction with a denominator of 100, we multiply both the numerator and denominator by 20:
(2 x 20) / (5 x 20) = 40/100
Since 40/100 means 40 out of 100, it's equivalent to 40%.
Practical Applications: Real-World Examples of 40%
Understanding the concept of 40% has numerous practical applications. Here are a few examples:
- Grades: If a student answers 8 out of 20 questions correctly on a test, their score is 40%.
- Discounts: A 40% discount on a $100 item means a reduction of $40, resulting in a final price of $60.
- Surveys: If 40% of respondents in a survey agree with a particular statement, it means that 40 out of every 100 respondents agree.
- Statistics: In data analysis, 40% could represent the proportion of a specific characteristic within a population.
Beyond 8/20: Exploring Related Percentage Calculations
Now that we understand how to convert 8/20 to a percentage, let's explore some related calculations:
- Finding 40% of a number: To find 40% of a number, multiply the number by 0.4 (which is the decimal equivalent of 40%). For example, 40% of 50 is 50 x 0.4 = 20.
- Calculating the original amount after a percentage increase or decrease: If an item increased by 40% to reach a price of $70, we can work backward to find the original price. Let's represent the original price as 'x'. The equation would be: x + 0.4x = 70. This simplifies to 1.4x = 70. Dividing both sides by 1.4 gives us x = $50. Therefore, the original price was $50.
- Converting percentages to fractions: To convert a percentage back into a fraction, divide the percentage by 100 and simplify the resulting fraction. For instance, 40% is 40/100, which simplifies to 2/5.
- Comparing percentages: When comparing percentages, it's crucial to ensure that they represent the same base value. For example, a 40% increase from 100 is different from a 40% increase from 200.
Frequently Asked Questions (FAQ)
-
Q: Is there a shortcut for converting fractions to percentages? A: Yes, the quickest method is to divide the numerator by the denominator and multiply the result by 100.
-
Q: Can I convert fractions with larger numbers into percentages using the same method? A: Absolutely. The process remains the same regardless of the size of the numerator and denominator.
-
Q: What if the resulting decimal is long and doesn't terminate? A: You can round the decimal to a certain number of decimal places for practical purposes. For instance, if you get 0.33333..., you might round it to 0.33 or 0.333, depending on the required level of precision.
-
Q: How do I convert percentages to decimals? A: To convert a percentage to a decimal, divide the percentage by 100. For example, 40% becomes 40/100 = 0.4.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages, as demonstrated with the example of 8/20, is a crucial mathematical skill. Understanding the underlying concepts and mastering the various methods presented here will not only help you solve problems related to percentages directly but also enhance your ability to analyze data, understand financial information, and confidently navigate various real-world scenarios where percentages play a vital role. By practicing these techniques and exploring the related percentage calculations, you can build a solid foundation for more advanced mathematical concepts. Remember, the key is to break down the problem into smaller, manageable steps, and to always double-check your work to ensure accuracy. With consistent practice, converting fractions to percentages will become second nature.
Latest Posts
Latest Posts
-
Dynamic Vs Static Equilibrium
Sep 24, 2025
-
75 Percent Of 60
Sep 24, 2025
-
102 Celsius To Fahrenheit
Sep 24, 2025
-
157 Pounds In Kilograms
Sep 24, 2025
-
Certificates Of Deposit Australia
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 8/20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.