8 X 2 3
renascent
Sep 22, 2025 · 6 min read
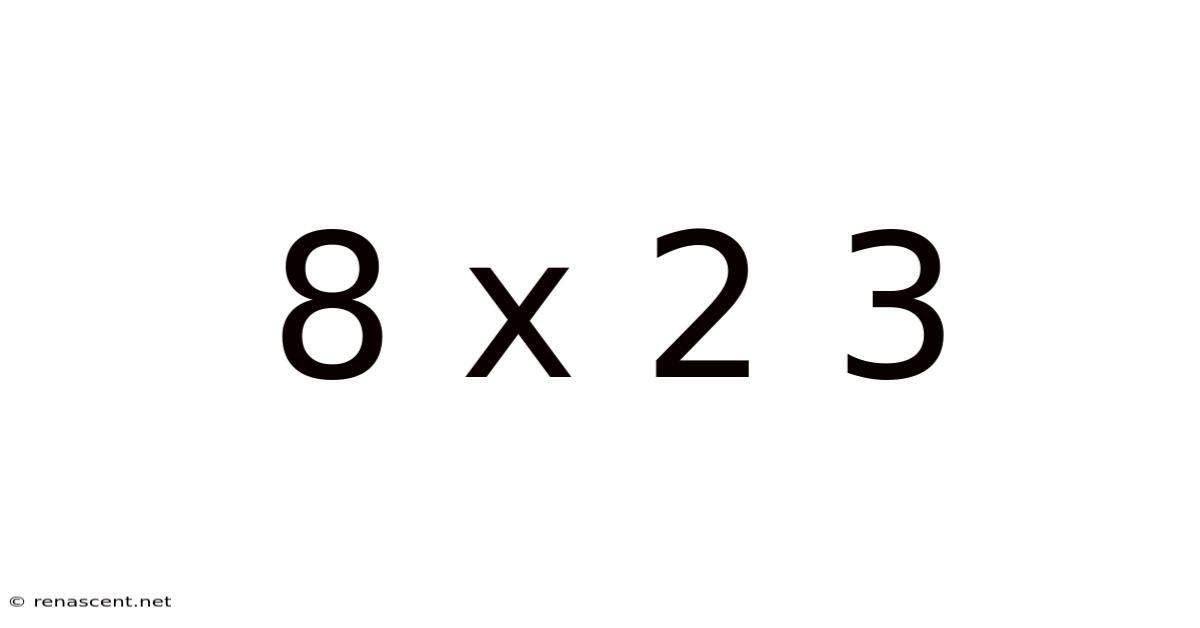
Table of Contents
Decoding 8 x 2³: A Deep Dive into Exponents, Order of Operations, and Practical Applications
This article explores the seemingly simple mathematical expression "8 x 2³," delving far beyond a basic calculation to uncover the underlying principles of exponents, the crucial role of order of operations (PEMDAS/BODMAS), and the widespread applications of these concepts in various fields. Understanding this seemingly simple equation unlocks a significant portion of mathematical literacy, crucial for success in numerous academic and professional pursuits.
Introduction: Unveiling the Mystery
The expression "8 x 2³" is more than just a numerical problem; it's a gateway to understanding fundamental mathematical concepts. At its core, it involves two key mathematical operations: multiplication and exponentiation. While seemingly straightforward, correctly solving this requires a solid grasp of the order of operations, a set of rules that dictates the sequence in which calculations should be performed. This article will systematically break down the solution, explain the underlying principles, and demonstrate the broader significance of these concepts. We will cover everything from the basics of exponents to real-world applications, ensuring a comprehensive understanding for readers of all levels.
Understanding Exponents: The Power of Powers
The core of "8 x 2³" lies in the exponent, represented by the superscript '3' in 2³. An exponent (also known as a power or index) indicates how many times a base number is multiplied by itself. In this case, 2³ means 2 multiplied by itself three times: 2 x 2 x 2 = 8. The number 2 is the base, and the number 3 is the exponent.
It's crucial to understand that exponents are not simply repeated addition. While 2 x 3 = 6, 2³ is not 2 + 2 + 2 = 6. The difference is significant and underlines the fundamental distinction between multiplication and exponentiation. Exponents lead to dramatically faster growth than simple multiplication, a concept central to understanding exponential growth and decay in various fields, from finance to biology.
Let's explore a few more examples to solidify this understanding:
- 3² = 3 x 3 = 9
- 5³ = 5 x 5 x 5 = 125
- 10⁴ = 10 x 10 x 10 x 10 = 10,000
These examples highlight the rapid increase in value as the exponent increases. This exponential growth is a powerful concept with far-reaching implications.
The Order of Operations: PEMDAS/BODMAS
To accurately solve "8 x 2³," we must adhere to the order of operations, a set of rules ensuring consistent results regardless of who performs the calculation. The most common mnemonics are PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) and BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both mnemonics represent the same order of operations.
Applying PEMDAS/BODMAS to our equation:
-
Exponents: First, we calculate the exponent: 2³ = 8.
-
Multiplication: Next, we perform the multiplication: 8 x 8 = 64.
Therefore, the solution to "8 x 2³" is 64. Ignoring the order of operations and performing the multiplication before the exponentiation (8 x 2 = 16, then 16³ = 4096) would yield an entirely incorrect answer. The order of operations is non-negotiable; it's the foundation of consistent mathematical calculations.
Beyond the Calculation: Real-World Applications
The principles behind "8 x 2³" extend far beyond simple arithmetic. Let's explore some real-world applications:
-
Compound Interest: In finance, compound interest calculations heavily rely on exponents. The formula for compound interest involves raising a base number (1 + interest rate) to the power of the number of compounding periods. Understanding exponents is crucial for accurately calculating future values of investments.
-
Exponential Growth and Decay: Many natural phenomena exhibit exponential growth or decay. Population growth, radioactive decay, and the spread of diseases often follow exponential patterns. The ability to model these using exponents allows for accurate predictions and informed decision-making.
-
Computer Science: Exponents play a vital role in computer science, particularly in algorithm analysis and data structure design. The efficiency of algorithms is often expressed using Big O notation, which frequently involves exponential terms.
-
Physics and Engineering: Exponential functions are ubiquitous in physics and engineering, describing phenomena like the decay of radioactive materials, the charging and discharging of capacitors, and the intensity of light or sound waves.
-
Biology: Exponential growth is a key concept in population biology, modeling the growth of bacterial colonies, the spread of viruses, and the dynamics of ecosystems.
-
Chemistry: Chemical reactions can exhibit exponential kinetics, where the rate of the reaction is influenced by exponential factors.
-
Economics: Economic growth models often utilize exponential functions to represent trends in GDP and other economic indicators.
Expanding the Scope: More Complex Expressions
Let's consider more complex expressions involving exponents and the order of operations:
-
(3 + 2)² x 5 - 10: Following PEMDAS/BODMAS, we first calculate the parentheses: (3 + 2) = 5. Then, we address the exponent: 5² = 25. Next, we perform the multiplication: 25 x 5 = 125. Finally, the subtraction: 125 - 10 = 115.
-
4³ ÷ 2² + 7 x 3: Here, we first solve the exponents: 4³ = 64 and 2² = 4. Next, we handle the division and multiplication from left to right: 64 ÷ 4 = 16 and 7 x 3 = 21. Finally, we perform the addition: 16 + 21 = 37.
These examples demonstrate the importance of meticulously adhering to the order of operations. A slight deviation can drastically alter the final result.
Frequently Asked Questions (FAQ)
-
What happens if I don't follow the order of operations? You'll likely obtain an incorrect answer. The order of operations is a fundamental rule in mathematics, ensuring consistency and accuracy.
-
Are there any exceptions to PEMDAS/BODMAS? While PEMDAS/BODMAS is a general guideline, there are some exceptions depending on the specific context. However, these are usually explicitly indicated using parentheses or other notations.
-
How can I improve my understanding of exponents? Practice is key! Work through numerous examples, try different problems, and gradually increase the complexity. Utilize online resources, textbooks, or educational videos.
-
Why are exponents so important? Exponents represent a concise way of expressing repeated multiplication and are crucial for modeling numerous real-world phenomena exhibiting exponential growth or decay.
Conclusion: Mastering the Fundamentals
The seemingly simple expression "8 x 2³" serves as a microcosm of fundamental mathematical principles. Understanding exponents, the order of operations, and their diverse applications empowers you to tackle more complex problems and appreciate the mathematical underpinnings of the world around us. From financial calculations to scientific modeling, these concepts are indispensable tools for critical thinking and problem-solving in various fields. By mastering these foundational concepts, you not only enhance your mathematical skills but also cultivate a deeper appreciation for the elegance and power of mathematics. Continuous practice and exploration are key to solidifying your understanding and unlocking the full potential of these vital mathematical tools. The journey of mathematical understanding is continuous, and this exploration of "8 x 2³" is just one step on that exciting path.
Latest Posts
Latest Posts
-
Does Acai Have Caffeine
Sep 22, 2025
-
500 Gm In Ounces
Sep 22, 2025
-
G Kg To Percentage
Sep 22, 2025
-
30 Divided By 12
Sep 22, 2025
-
1 12 Of 12
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 8 X 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.