8 X 3 10
renascent
Sep 20, 2025 · 6 min read
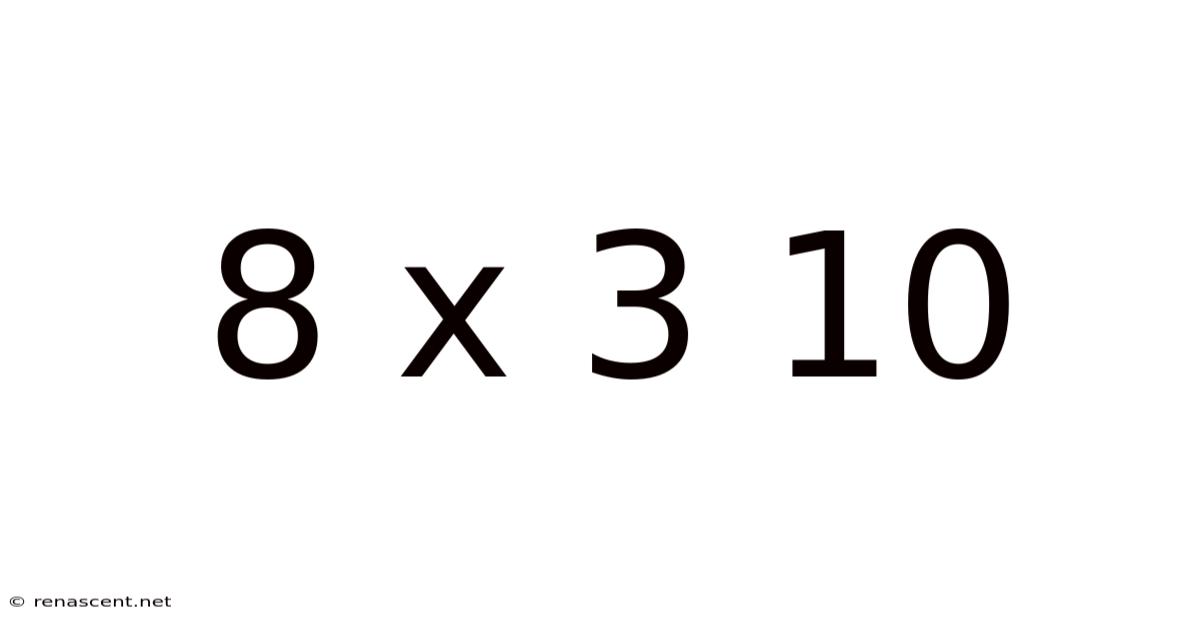
Table of Contents
Decoding the Enigma: Understanding the Mathematical Expression "8 x 3 = 10"
This article delves into the seemingly paradoxical statement "8 x 3 = 10." While in standard base-10 arithmetic this equation is false (the correct answer is 24), the expression hints at alternative mathematical systems or contexts where such a result might hold true. We'll explore different mathematical frameworks, potential interpretations, and the broader significance of understanding mathematical ambiguity. This exploration will reveal the richness and flexibility of mathematical thought beyond the familiar rules we learn in school.
Introduction: Beyond Standard Arithmetic
The statement "8 x 3 = 10" immediately strikes us as incorrect based on our ingrained understanding of multiplication in the decimal (base-10) system. However, the beauty of mathematics lies in its ability to adapt and represent different systems and concepts. This seemingly simple equation opens a door to explore several possibilities: different number bases, modular arithmetic, and even symbolic representations that go beyond numerical values. Understanding the context is crucial in deciphering the meaning behind such unconventional equations.
1. Number Bases: A Foundation of Mathematical Representation
Our everyday arithmetic operates within the decimal or base-10 system, utilizing ten digits (0-9) to represent numbers. However, other number bases exist, each with its own unique set of rules. The expression "8 x 3 = 10" could potentially be true within a different number base.
Let's consider a base-n system, where n represents the number of unique digits used. In base-10, n is 10. Let's explore a simpler base, like base-10:
- Base-10 (Decimal): As discussed, 8 x 3 = 24 in base-10.
Now, let's investigate a base-n system where the result could be 10. Let's work backward from the result to see if a specific base allows us to get to 10. If "8 x 3 = 10" in base-n, then we are looking for a base where 24 (in base-10) converts to 10. To do this, we need to convert the number 24 (base-10) to its equivalent in base-n.
In a base-n system, a number like 10 would be understood as 1n<sup>1</sup> + 0n<sup>0</sup> = n. To find our base, we could set up the equation:
n = 24 (Base-10)
This means we're looking for a base where the value '10' represents 24 in base-10. There isn't a whole number solution to this equation. The value of 'n' would be approximately 24. Therefore, a whole number base-n system does not allow "8 x 3 = 10".
The closest we can get to representing 24 as a two-digit number in a different base involves finding factors of 24 that could represent digits in the number system. However, none of these factors would allow us to express 24 in the form "10" in any integer base.
2. Modular Arithmetic: Exploring Remainders
Modular arithmetic, also known as clock arithmetic, focuses on the remainders after division. The expression "8 x 3 = 10" might hold true within a specific modulus.
Let's consider a modulus m. The expression "a ≡ b (mod m)" means that a and b have the same remainder when divided by m. We are looking for a modulus m where:
24 ≡ 10 (mod m)
This equation implies that 24 - 10 = 14 must be divisible by m. The divisors of 14 are 1, 2, 7, and 14. This means, for example, in modulo 7:
24 ÷ 7 = 3 with a remainder of 3. 10 ÷ 7 = 1 with a remainder of 3.
Therefore, 24 ≡ 10 (mod 7). Although "8 x 3 = 10" isn't directly true in modulo 7, we find a relationship between the results when we examine the remainders after division by the modulus.
This illustrates that in specific modular arithmetic systems, we might find congruence relationships that appear similar to the initial statement. However, this is a result of focusing on remainders rather than absolute values.
3. Beyond Numerical Values: Symbolic Representation
The expression "8 x 3 = 10" can be interpreted as a symbolic representation rather than a strictly numerical equation. In this case, "8," "3," and "10" might represent abstract quantities or concepts, and the multiplication sign ("x") might represent a specific operation defined within a system distinct from standard arithmetic.
For instance, in a hypothetical system, "8" could represent a certain set of attributes, "3" another, and "10" could represent the combination of those attributes under the defined operation. Without specifying the system's rules, the equation remains open to interpretation.
This approach opens up possibilities in areas like abstract algebra, where mathematicians work with structures that are not limited to the familiar numbers we often use in calculations. It highlights the versatility of mathematical symbols to represent diverse concepts.
4. Potential Applications and Further Exploration
While "8 x 3 = 10" is not true in standard arithmetic, exploring its potential interpretations offers valuable insights into different mathematical systems. The concept of number bases and modular arithmetic, for example, has widespread applications:
- Computer Science: Number bases like binary (base-2), octal (base-8), and hexadecimal (base-16) are fundamental to computer programming and data representation.
- Cryptography: Modular arithmetic plays a crucial role in cryptographic systems for securing data.
- Abstract Algebra: Exploring systems beyond standard arithmetic contributes to understanding abstract structures and mathematical frameworks.
Further research into abstract algebra, group theory, and ring theory will help unveil more complex mathematical contexts where such expressions might gain significance under specific rule sets.
Frequently Asked Questions (FAQ)
-
Q: Is "8 x 3 = 10" ever true? A: No, it is not true in standard base-10 arithmetic. However, it might hold true in a specific context within a different number system or under different operational definitions.
-
Q: What mathematical concepts are relevant to this expression? A: Number bases, modular arithmetic, abstract algebra, and symbolic representation are key concepts.
-
Q: Why is understanding this seemingly false statement important? A: It emphasizes the flexibility and scope of mathematics beyond standard arithmetic, opening doors to different systems and frameworks.
-
Q: Are there real-world applications of exploring alternative number systems? A: Yes, particularly in computer science and cryptography, where different number bases and modular arithmetic are extensively used.
Conclusion: The Power of Context in Mathematics
The seemingly simple equation "8 x 3 = 10" serves as a powerful reminder of the richness and versatility of mathematics. While false in standard base-10 arithmetic, the expression opens opportunities to explore diverse mathematical concepts like number bases, modular arithmetic, and symbolic representation. Understanding the context is crucial to interpreting such statements and appreciating the broader scope of mathematical thinking. By exploring these alternative frameworks, we gain a deeper understanding of the underlying principles of mathematics and its applicability across various fields. The initial incorrect equation acts as a gateway to a deeper appreciation for the diverse ways in which mathematical concepts can be used and understood. Further investigation into these areas will reveal even more profound connections and applications of these systems. The apparent paradox of "8 x 3 = 10" becomes a catalyst for intellectual exploration and a testament to the enduring power of mathematical reasoning.
Latest Posts
Latest Posts
-
12 Cm In Mm
Sep 20, 2025
-
Auguries Of Innocence Poem
Sep 20, 2025
-
9 27 Simplest Form
Sep 20, 2025
-
Braun Ear Thermometer Caps
Sep 20, 2025
-
806 Divided By 4
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 8 X 3 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.