80 Percent Of 50
renascent
Sep 23, 2025 · 6 min read
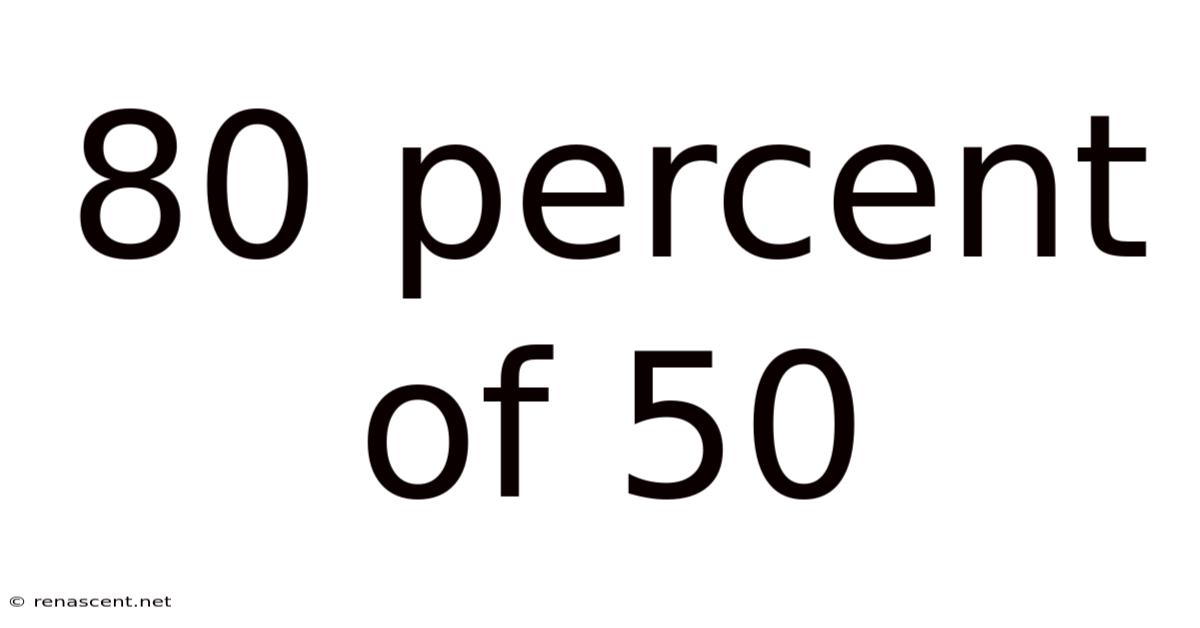
Table of Contents
Decoding 80% of 50: A Comprehensive Guide to Percentages
Finding 80% of 50 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying concepts of percentages is crucial, not just for solving this specific problem, but for navigating countless everyday situations involving discounts, taxes, grades, and more. This article will delve deep into calculating 80% of 50, explaining the process in multiple ways, exploring the broader context of percentages, and addressing frequently asked questions. By the end, you'll not only know the answer but also possess a solid understanding of percentage calculations.
Understanding Percentages: The Foundation
Before tackling the problem directly, let's establish a firm grasp of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, 80% means 80 out of 100, or 80/100. This fraction can be simplified to 4/5.
Method 1: Using Decimal Conversion
This is arguably the most straightforward method for calculating 80% of 50. We convert the percentage to its decimal equivalent and then multiply it by the number.
-
Convert the percentage to a decimal: To convert 80% to a decimal, we divide it by 100: 80 ÷ 100 = 0.8
-
Multiply the decimal by the number: Now, we multiply the decimal equivalent (0.8) by 50: 0.8 x 50 = 40
Therefore, 80% of 50 is $\boxed{40}$.
Method 2: Using Fraction Conversion
This method leverages the fractional representation of percentages.
-
Express the percentage as a fraction: As mentioned earlier, 80% can be expressed as the fraction 80/100, which simplifies to 4/5.
-
Multiply the fraction by the number: We multiply the simplified fraction (4/5) by 50: (4/5) x 50 = (4 x 50) / 5 = 200 / 5 = 40
Again, we arrive at the answer: 80% of 50 is $\boxed{40}$.
Method 3: Proportion Method
This method uses the concept of proportions to solve the problem. We set up a proportion where one ratio represents the percentage and the other represents the unknown part of the whole.
-
Set up the proportion: We set up a proportion as follows:
80/100 = x/50
Where 'x' represents the unknown value (80% of 50).
-
Cross-multiply and solve: To solve for 'x', we cross-multiply:
100x = 80 x 50
100x = 4000
x = 4000 / 100
x = 40
Therefore, 80% of 50 is $\boxed{40}$.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital for navigating various real-world scenarios. Here are a few examples:
-
Discounts: Stores frequently offer discounts, often expressed as percentages. For instance, a 20% discount on a $100 item means you'll save 20% of $100, or $20.
-
Taxes: Sales taxes and income taxes are calculated as percentages of the total amount. A 7% sales tax on a $50 purchase, for example, would be $3.50 (7% of $50).
-
Grades: Many academic grading systems use percentages to represent a student's performance. A score of 85% on a test typically indicates that the student answered 85 out of 100 questions correctly.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are typically expressed as percentages. A 5% interest rate on a $1000 investment would mean you earn $50 in interest per year.
-
Statistics and Data Analysis: Percentages are essential in presenting and interpreting statistical data. For example, if a survey indicates that 60% of respondents prefer a particular product, this provides valuable information about consumer preferences.
Beyond the Basics: Understanding Percentage Increase and Decrease
While calculating a percentage of a number is fundamental, it's also important to understand percentage increases and decreases. These calculations are often used to analyze changes over time or compare different values.
Percentage Increase: This calculates the increase in a value relative to its original value. The formula is:
[(New Value - Original Value) / Original Value] x 100%
Percentage Decrease: This calculates the decrease in a value relative to its original value. The formula is:
[(Original Value - New Value) / Original Value] x 100%
Troubleshooting Common Percentage Calculation Errors
Several common mistakes can occur when working with percentages. Here are some to watch out for:
-
Incorrect Decimal Conversion: Ensuring you accurately convert percentages to decimals (by dividing by 100) is crucial. A simple mistake here can significantly impact the final result.
-
Mixing Up Percentages and Decimals: Keeping track of whether you're working with a percentage or its decimal equivalent is essential. Avoid accidentally multiplying a number by a percentage instead of its decimal equivalent.
-
Incorrect Order of Operations: When working with multiple operations (addition, subtraction, multiplication, division), follow the order of operations (PEMDAS/BODMAS) to ensure accuracy.
Frequently Asked Questions (FAQ)
Q: Can I calculate 80% of 50 mentally?
A: Yes, with practice, you can. Consider that 80% is 4/5, and finding 1/5 of 50 is 10. Therefore, 4/5 of 50 is 4 x 10 = 40.
Q: What if I need to calculate a different percentage of 50?
A: The methods described above (decimal conversion, fraction conversion, proportion method) can be applied to calculate any percentage of 50 (or any other number). Simply substitute the desired percentage into the equations.
Q: Are there any online calculators that can help with percentage calculations?
A: Yes, many online calculators are readily available that can perform percentage calculations quickly and efficiently. However, understanding the underlying principles is still crucial for solving problems effectively.
Q: Why is understanding percentages important in everyday life?
A: Percentages are used extensively in various aspects of daily life, from financial transactions (discounts, taxes, interest rates) to academic assessments and data analysis. A strong understanding of percentages empowers you to make informed decisions and interpret information effectively.
Q: How can I improve my skills in percentage calculations?
A: Practice is key. Solve various percentage problems using different methods. Start with simple problems and gradually move to more complex ones. Online resources and practice workbooks can further enhance your understanding and skills.
Conclusion
Calculating 80% of 50, while seemingly straightforward, provides a valuable entry point into the broader world of percentage calculations. Mastering the methods outlined here – decimal conversion, fraction conversion, and the proportion method – will equip you with the skills to tackle a wide range of percentage problems encountered in everyday life, academic studies, and professional settings. Remember that consistent practice and a solid understanding of the underlying concepts are crucial for developing proficiency in percentage calculations. By understanding these fundamentals, you’ll not only find the answer to “80% of 50” easily but also enhance your numerical literacy significantly.
Latest Posts
Latest Posts
-
5000 Meters To Kilometers
Sep 23, 2025
-
125 Lbs En Kg
Sep 23, 2025
-
7 2 Divided By 2
Sep 23, 2025
-
2 1 2 As Decimal
Sep 23, 2025
-
317 Divided By 8
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 80 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.