9 15 As Decimal
renascent
Sep 22, 2025 · 5 min read
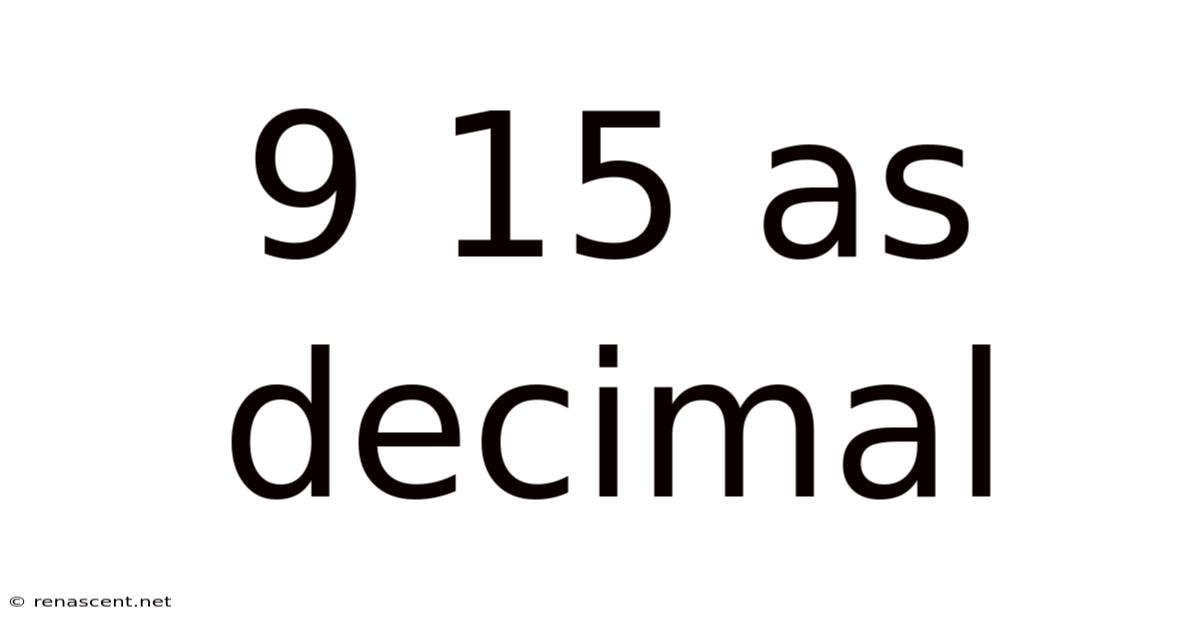
Table of Contents
Unveiling the Mystery: 9/15 as a Decimal
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the fraction 9/15 to its decimal representation, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also cover related concepts and frequently asked questions to provide a thorough understanding of this seemingly simple yet important topic.
Introduction: Fractions and Decimals – A Bridge Between Concepts
Fractions and decimals are two different ways of representing parts of a whole. A fraction expresses a part as a ratio of two numbers (the numerator and the denominator), while a decimal expresses a part using a base-ten system, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. Converting between fractions and decimals is crucial for various mathematical operations and applications. The fraction 9/15 is a common example used to illustrate this conversion process. This article will provide a clear, step-by-step guide to convert 9/15 into its decimal equivalent, alongside explanations and related concepts.
Method 1: Simplifying the Fraction Before Conversion
The most efficient way to convert 9/15 to a decimal is to first simplify the fraction. This involves finding the greatest common divisor (GCD) of the numerator (9) and the denominator (15). The GCD of 9 and 15 is 3. Dividing both the numerator and the denominator by the GCD, we get:
9 ÷ 3 = 3 15 ÷ 3 = 5
This simplifies the fraction to 3/5. Now, converting 3/5 to a decimal is much easier.
Method 2: Long Division
Once we have the simplified fraction 3/5, we can use long division to convert it to a decimal. The numerator (3) becomes the dividend, and the denominator (5) becomes the divisor.
0.6
5 | 3.0
3.0
---
0
We add a decimal point and a zero to the dividend (3) to perform the division. 5 goes into 30 six times (5 x 6 = 30). Therefore, 3/5 is equal to 0.6.
Therefore, 9/15 simplified to 3/5, which equals 0.6 as a decimal.
Method 3: Converting Directly (Without Simplification)
While simplifying the fraction first is generally recommended, it's possible to convert 9/15 directly to a decimal using long division. This method is slightly more complex, but it demonstrates the process without simplification.
0.6
15 | 9.00
9.0
---
0
As you can see, even without simplifying, the result is still 0.6. However, simplifying makes the long division process significantly easier.
Understanding the Decimal Representation: Terminating vs. Repeating Decimals
In this case, 9/15 converts to a terminating decimal, meaning the decimal representation ends after a finite number of digits (0.6). Not all fractions produce terminating decimals. Some fractions result in repeating decimals, where one or more digits repeat infinitely. For instance, 1/3 converts to 0.3333..., where the digit 3 repeats indefinitely. The difference lies in the denominator of the fraction in its simplest form. If the denominator only contains prime factors of 2 and/or 5 (the prime factors of 10), the decimal will terminate. Otherwise, it will repeat.
Expanding the Understanding: Working with More Complex Fractions
Let's consider a slightly more complex example to reinforce the concept. Let's convert the fraction 17/20 to a decimal.
First, we check if it can be simplified. The GCD of 17 and 20 is 1, so the fraction is already in its simplest form. Now, we use long division:
0.85
20 | 17.00
16.0
---
1.00
1.00
---
0
Therefore, 17/20 equals 0.85. This is another example of a terminating decimal.
Practical Applications of Fraction-to-Decimal Conversion
The ability to convert fractions to decimals is essential in various real-world scenarios, including:
- Financial Calculations: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals.
- Scientific Measurements: Many scientific measurements and calculations involve fractions that need to be expressed as decimals.
- Engineering and Construction: Precise measurements and calculations in engineering and construction require the ability to convert fractions to decimals.
- Data Analysis: Converting fractions to decimals is often necessary when working with data in spreadsheets or statistical software.
Frequently Asked Questions (FAQs)
Q1: What if the fraction is a mixed number?
A: If you have a mixed number (e.g., 2 1/4), convert it to an improper fraction first (9/4 in this case), and then follow the long division method.
Q2: How do I convert a repeating decimal back into a fraction?
A: This process involves algebraic manipulation. You represent the repeating decimal using variables and equations to solve for the fractional equivalent.
Q3: Are there any online calculators or tools to help with this conversion?
A: Yes, many online calculators can perform fraction-to-decimal conversions instantly. However, understanding the underlying process is crucial for building a strong mathematical foundation.
Q4: Why is simplifying the fraction beneficial before conversion?
A: Simplifying reduces the complexity of the long division, making the calculation faster and less prone to errors.
Q5: What are some common mistakes to avoid when converting fractions to decimals?
A: Common mistakes include incorrect simplification of fractions, errors in long division, and forgetting to add a decimal point and zeros when needed.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions like 9/15 to decimals is a fundamental skill in mathematics. Understanding the process, whether through simplification and long division or direct long division, is vital for various applications. This guide has detailed the steps involved, highlighted the importance of understanding terminating and repeating decimals, and explored various practical applications. By mastering this skill, you'll be well-equipped to tackle more complex mathematical problems and confidently navigate various numerical situations in your academic and professional life. Remember to practice regularly to reinforce your understanding and improve your efficiency in performing these conversions. The more you practice, the more intuitive and effortless this process will become.
Latest Posts
Latest Posts
-
Does Acai Have Caffeine
Sep 22, 2025
-
500 Gm In Ounces
Sep 22, 2025
-
G Kg To Percentage
Sep 22, 2025
-
30 Divided By 12
Sep 22, 2025
-
1 12 Of 12
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 9 15 As Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.