9 X 5 8
renascent
Sep 19, 2025 · 5 min read
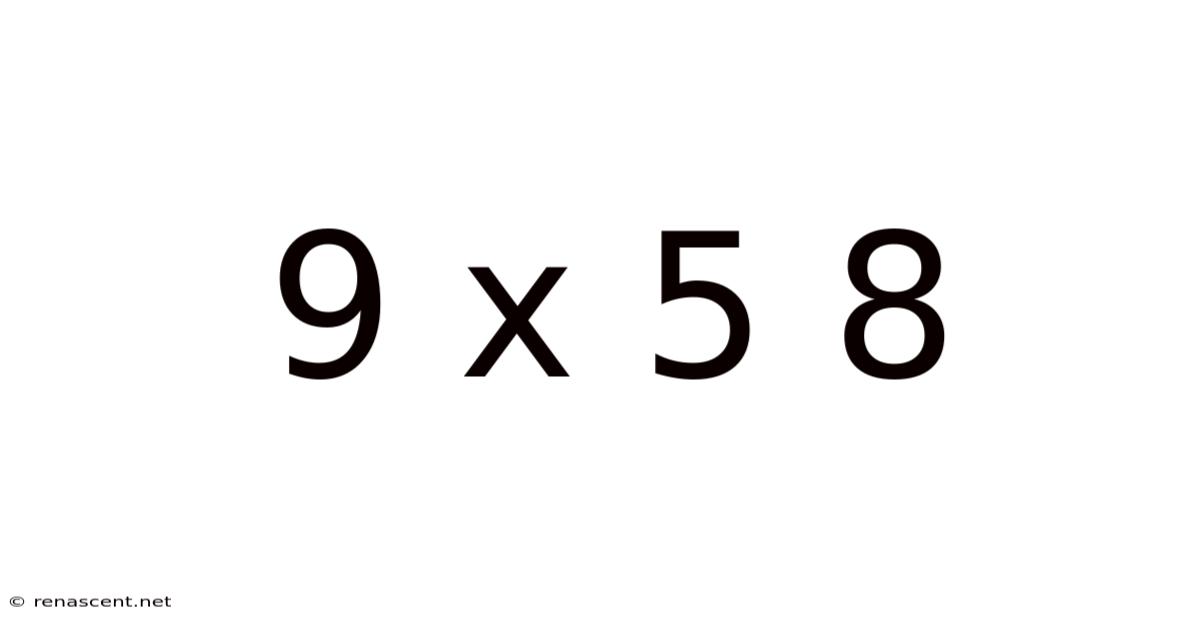
Table of Contents
Decoding 9 x 5 = 45: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple equation, 9 x 5 = 45, delving far beyond the basic arithmetic to uncover its significance in various mathematical contexts and real-world applications. We'll unpack the fundamentals of multiplication, explore different methods for solving this equation, examine its role in more complex mathematical concepts, and finally, consider its practical applications in everyday life. Understanding this simple equation opens doors to a deeper appreciation of mathematics and its pervasive influence on our world.
Understanding the Fundamentals: What is Multiplication?
Multiplication, at its core, is repeated addition. When we say 9 x 5, we're essentially asking: "What is the sum of nine fives?" This can be visually represented as nine groups of five objects each. Imagine nine bags, each containing five apples. Counting all the apples would give you the answer: 45.
This basic understanding forms the foundation for more advanced mathematical operations. Multiplication is commutative (meaning 9 x 5 is the same as 5 x 9), associative (allowing for grouping in more complex equations), and distributive (allowing multiplication across addition or subtraction). These properties are crucial for solving more complex problems.
Methods for Solving 9 x 5 = 45
While the answer is readily apparent to most, understanding the different methods for arriving at 45 reinforces the underlying principles of multiplication.
-
Repeated Addition: The most fundamental approach: 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 45. This method clearly illustrates the concept of multiplication as repeated addition.
-
Multiplication Table: Most students learn their multiplication tables by rote memorization. The 9 times table, in particular, is often memorized, making the answer to 9 x 5 readily available. This method emphasizes quick recall and efficiency.
-
Using Arrays: Visually representing the multiplication problem using an array of dots or objects. Imagine a grid with 9 rows and 5 columns. Counting the total number of squares in the grid would yield 45. This method is particularly useful for visualizing the concept of multiplication, especially for younger learners.
-
Distributive Property: This approach breaks down the problem into smaller, more manageable parts. For instance, we could think of 9 x 5 as (10 - 1) x 5. Using the distributive property, this becomes (10 x 5) - (1 x 5) = 50 - 5 = 45. This illustrates a more advanced understanding of mathematical properties.
-
Skip Counting: Counting by fives nine times: 5, 10, 15, 20, 25, 30, 35, 40, 45. This method connects multiplication to counting and provides a practical way to solve the problem.
9 x 5 in the Broader Context of Mathematics
The seemingly simple equation 9 x 5 = 45 plays a surprisingly significant role in several branches of mathematics:
-
Algebra: Multiplication is a fundamental operation in algebra. Understanding 9 x 5 helps in solving algebraic equations involving variables and constants. For example, if 9x = 45, solving for x requires an understanding of the inverse operation of multiplication—division.
-
Geometry: Calculating the area of a rectangle relies heavily on multiplication. If a rectangle has a length of 9 units and a width of 5 units, its area is 9 x 5 = 45 square units. This simple equation forms the basis for calculating areas of more complex shapes.
-
Calculus: While seemingly distant, the principles underlying multiplication are foundational to calculus. The concept of limits, integrals, and derivatives all involve understanding the relationships between numbers, similar to those demonstrated in basic multiplication.
-
Number Theory: The factors of 45 (1, 3, 5, 9, 15, 45) and its multiples are explored within number theory. Understanding the prime factorization of 45 (3² x 5) provides insights into its divisibility and relationships with other numbers.
-
Statistics and Probability: Multiplication is used extensively in calculating probabilities and combinations. Understanding this fundamental operation is critical for solving various statistical problems.
Real-World Applications of 9 x 5 = 45
The practical applications of this seemingly simple equation are numerous and diverse:
-
Shopping: If apples cost $5 each, and you buy 9 apples, the total cost is 9 x 5 = $45. This is a simple yet ubiquitous application of multiplication in daily life.
-
Construction: Calculating the number of bricks needed for a wall or the amount of paint required for a room often involves multiplication.
-
Cooking and Baking: Many recipes require multiplying ingredient quantities. If a recipe calls for 5 cups of flour and you want to make 9 times the recipe, you'll need 9 x 5 = 45 cups of flour.
-
Travel and Distance: Calculating the total distance traveled based on speed and time often involves multiplication.
-
Finance and Budgeting: Calculating monthly expenses, interest rates, or investment returns often involves multiplication.
Frequently Asked Questions (FAQ)
-
What is the inverse operation of multiplication? Division. If 9 x 5 = 45, then 45 ÷ 9 = 5 and 45 ÷ 5 = 9.
-
Why is 9 x 5 the same as 5 x 9? This illustrates the commutative property of multiplication – the order of the numbers doesn't affect the result.
-
How can I learn my multiplication tables faster? Practice regularly, use flashcards, and try different memorization techniques. Visual aids, like arrays, can also help.
-
Are there any tricks for remembering the 9 times table? Yes! One common trick involves using your fingers. To multiply 9 by any number from 1 to 10, hold down that finger number. The number of fingers to the left of the held-down finger represents the tens digit, and the number of fingers to the right represents the ones digit.
-
How does multiplication relate to other mathematical concepts? Multiplication is fundamental to many mathematical concepts, including division, fractions, decimals, algebra, geometry, and calculus.
Conclusion: The Enduring Significance of a Simple Equation
The equation 9 x 5 = 45, while seemingly basic, serves as a gateway to a deeper understanding of mathematics and its pervasive influence on our lives. From the fundamental concepts of repeated addition to its applications in complex mathematical fields and everyday scenarios, this simple equation highlights the power and beauty of mathematics. Mastering this seemingly simple equation, and its underlying principles, lays a strong foundation for more advanced mathematical concepts and problem-solving skills, proving its enduring significance in education and beyond. The seemingly simple act of multiplying 9 by 5 opens a world of possibilities, underscoring the importance of even the most basic mathematical foundations. Understanding this equation isn't just about getting the right answer; it's about grasping the underlying principles that govern a significant portion of our world.
Latest Posts
Latest Posts
-
153 Pounds To Kilos
Sep 19, 2025
-
Can Mute People Laugh
Sep 19, 2025
-
1 50 As A Percentage
Sep 19, 2025
-
255 Minutes To Hours
Sep 19, 2025
-
10 Of 250 000
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 9 X 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.