90 Divided By 15
renascent
Sep 13, 2025 · 6 min read
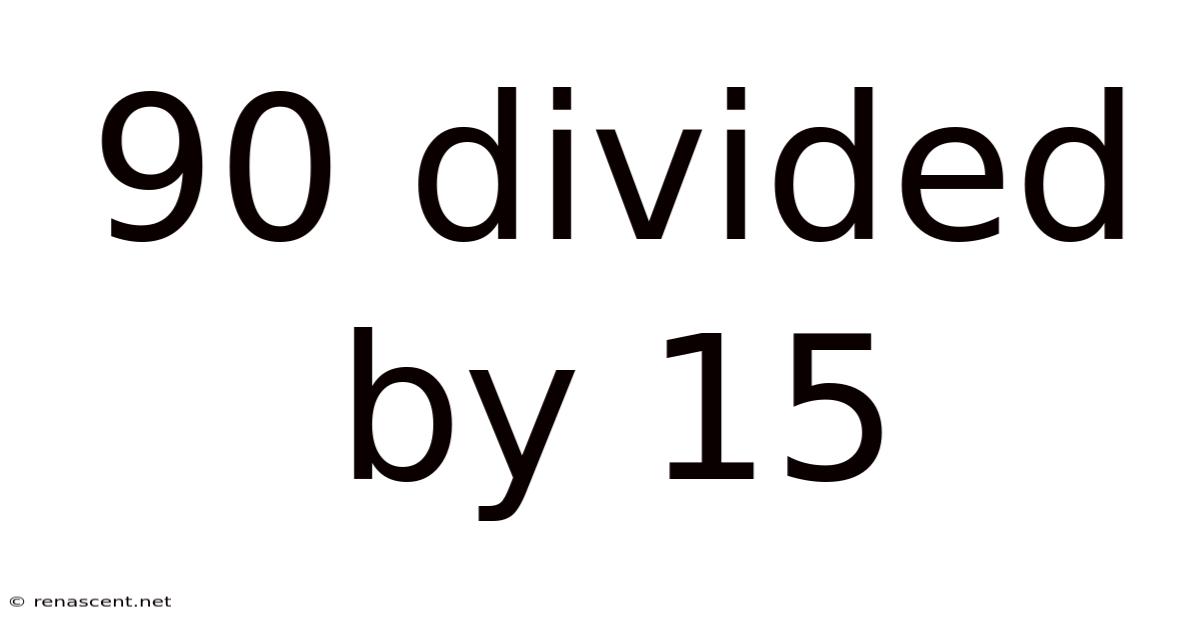
Table of Contents
90 Divided by 15: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 90 divided by 15, delving beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and related concepts. Understanding this seemingly basic operation opens doors to a broader appreciation of division, its role in various fields, and its connection to other mathematical concepts. We will cover the process, explore different methods of solving the problem, and discuss real-world scenarios where this type of calculation is essential.
Understanding Division: The Foundation
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the inverse of multiplication; it answers the question, "How many times does one number go into another?" In the context of 90 divided by 15 (written as 90 ÷ 15 or 90/15), we're asking how many times 15 fits into 90.
The parts of a division problem have specific names:
- Dividend: The number being divided (90 in this case).
- Divisor: The number we're dividing by (15 in this case).
- Quotient: The result of the division (the answer).
- Remainder: The amount left over if the divisor doesn't divide the dividend perfectly. In this case, there will be no remainder.
Calculating 90 Divided by 15: Methods and Approaches
There are several ways to solve 90 ÷ 15:
1. Long Division: This is a traditional method, particularly useful for larger numbers.
6
15 | 90
-90
--
0
We start by asking how many times 15 goes into 9 (the first digit of the dividend). It doesn't go in at all, so we move to the next digit, making it 90. 15 goes into 90 six times (15 x 6 = 90). Subtracting 90 from 90 leaves a remainder of 0. Therefore, the quotient is 6.
2. Repeated Subtraction: This method involves repeatedly subtracting the divisor from the dividend until we reach zero or a number smaller than the divisor.
90 - 15 = 75 75 - 15 = 60 60 - 15 = 45 45 - 15 = 30 30 - 15 = 15 15 - 15 = 0
We subtracted 15 six times, hence the answer is 6.
3. Factoring and Simplification: This method leverages the relationship between multiplication and division. We can find factors of both 90 and 15 to simplify the calculation.
90 = 2 x 3 x 3 x 5 15 = 3 x 5
Notice that 3 x 5 is a common factor in both numbers. We can cancel these out:
(2 x 3 x 3 x 5) / (3 x 5) = 2 x 3 = 6
This method demonstrates the underlying principles of simplification and emphasizes the interconnectedness of mathematical operations.
4. Using a Calculator: The simplest method for this specific problem, and a valuable tool for more complex division problems. Inputting 90 ÷ 15 into a calculator will instantly provide the answer, 6. While convenient, understanding the underlying methods is crucial for developing a stronger mathematical foundation.
Real-World Applications of Division: Beyond the Classroom
Division isn't just a classroom exercise; it's a fundamental operation used extensively in various fields:
- Finance: Calculating interest rates, dividing profits amongst shareholders, determining the cost per unit of a product. Imagine dividing total sales revenue by the number of units sold to find the average price per unit. This calculation is crucial for businesses to understand profitability and pricing strategies.
- Engineering: Calculating material requirements, dividing distances, determining the load-bearing capacity of structures. Engineers frequently use division to determine proportions, ratios, and optimal configurations for designs and projects. For example, dividing the total weight of a bridge by the number of support pillars helps in determining the load per pillar.
- Science: Converting units (e.g., converting kilometers to meters), determining average speeds, calculating concentrations of solutions. Scientific measurements and calculations routinely involve division to normalize data, determine averages, and perform conversions between units. For instance, dividing the total distance traveled by the time taken provides the average speed.
- Everyday Life: Sharing items equally among friends, splitting bills, calculating unit prices at the grocery store, figuring out how many servings are in a recipe. From everyday tasks to more complex problem-solving, division is an essential life skill.
- Computer Science: In computer programming, division is used extensively in algorithms, data processing, and calculations involved in various software applications. It forms the basis of many computations involved in graphics, simulations, and other advanced applications.
Exploring Related Mathematical Concepts
Understanding 90 ÷ 15 provides a springboard to explore several interconnected mathematical concepts:
- Factors and Multiples: The divisor (15) is a factor of the dividend (90), meaning 15 divides 90 evenly without a remainder. Conversely, 90 is a multiple of 15. Exploring factors and multiples deepens the understanding of number relationships.
- Fractions: The division problem 90 ÷ 15 can be represented as the fraction 90/15. Simplifying this fraction to its lowest terms (6/1 or simply 6) illustrates the connection between division and fractions.
- Ratios and Proportions: Division is fundamental to understanding ratios and proportions. For example, the ratio of 90 to 15 is 6:1, which can be simplified from 90:15. Proportions involve finding equivalent ratios.
- Algebra: Division plays a crucial role in solving algebraic equations. It's used to isolate variables and find unknown values.
Frequently Asked Questions (FAQ)
- What if the divisor doesn't divide the dividend perfectly? If the divisor doesn't divide the dividend evenly, there will be a remainder. For example, 92 ÷ 15 would result in a quotient of 6 and a remainder of 2 (15 x 6 + 2 = 92).
- What is the significance of the remainder? The remainder represents the amount left over after dividing as much as possible. Its importance depends on the context. In some cases, it's irrelevant; in others, it might need to be considered. For instance, if dividing cookies among friends, the remainder represents the cookies left over.
- Are there different ways to represent division? Yes, division can be represented in several ways: 90 ÷ 15, 90/15, 15)90 (long division format). Each notation serves a specific purpose and offers different perspectives on the operation.
Conclusion: The Power of Simple Division
While the calculation of 90 divided by 15 might seem trivial at first glance, a deeper exploration reveals its fundamental role in mathematics and its extensive applications in various fields. Understanding the different methods of solving this problem, along with the related concepts and real-world applications, highlights the importance of mastering this seemingly basic arithmetic operation. It's more than just finding the answer; it's about understanding the underlying mathematical principles and their significance in problem-solving and critical thinking. The seemingly simple 6 is a gateway to a much broader understanding of the mathematical world.
Latest Posts
Latest Posts
-
480 Seconds To Minutes
Sep 13, 2025
-
83 F In Celsius
Sep 13, 2025
-
83 5 Kilos In Pounds
Sep 13, 2025
-
7 8 In Half
Sep 13, 2025
-
X2 X 3 0
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 90 Divided By 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.