91 Divided By 7
renascent
Sep 25, 2025 · 6 min read
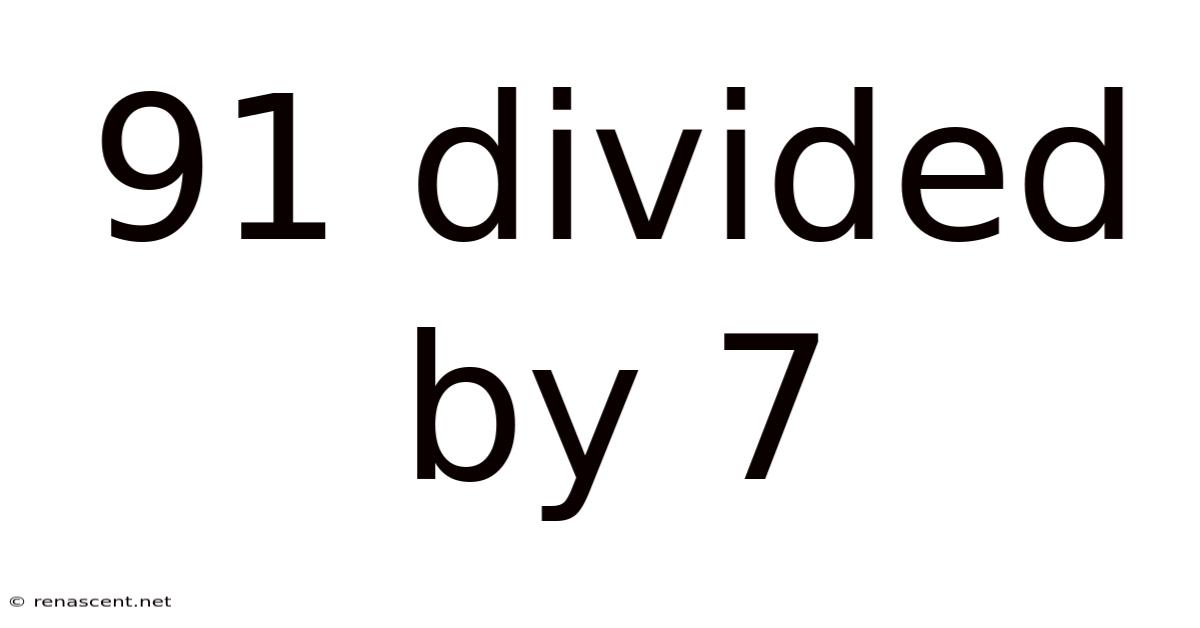
Table of Contents
Unpacking 91 Divided by 7: A Deep Dive into Division
The seemingly simple question, "What is 91 divided by 7?", opens the door to a fascinating exploration of division, its underlying principles, and its practical applications. While the answer itself is straightforward – 13 – the journey to understanding how we arrive at this answer reveals a wealth of mathematical concepts crucial for building a strong foundation in arithmetic. This article delves into the intricacies of this division problem, exploring various methods of solving it, discussing the underlying mathematical concepts, and addressing frequently asked questions. This comprehensive guide is perfect for students seeking a deeper understanding of division, as well as anyone curious about the elegance and practicality of mathematical operations.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. In the context of 91 divided by 7 (often written as 91 ÷ 7, 91/7, or <sup>91</sup>⁄<sub>7</sub>), we are asking: "How many times does 7 fit into 91?" The number being divided (91) is called the dividend, the number we are dividing by (7) is the divisor, and the result (13) is the quotient. Understanding these terms is fundamental to grasping the concept of division.
Methods for Solving 91 ÷ 7
There are several ways to solve 91 ÷ 7, catering to different learning styles and mathematical comfort levels. Let's explore a few:
1. Long Division
Long division is a standard algorithm taught in schools. It's a systematic approach that breaks down the division into smaller, manageable steps:
-
Set up the problem: Write the dividend (91) inside the long division symbol (⟌) and the divisor (7) outside.
-
Divide: Determine how many times the divisor (7) goes into the first digit of the dividend (9). It goes once (7 x 1 = 7). Write the "1" above the 9.
-
Multiply: Multiply the quotient digit (1) by the divisor (7): 1 x 7 = 7.
-
Subtract: Subtract the result (7) from the first digit of the dividend (9): 9 - 7 = 2.
-
Bring down: Bring down the next digit of the dividend (1) to create the number 21.
-
Repeat: Now, determine how many times the divisor (7) goes into 21. It goes three times (7 x 3 = 21). Write the "3" above the 1.
-
Multiply and Subtract: Multiply 3 by 7 (21) and subtract it from 21 (21 - 21 = 0).
-
Result: The result is the number formed by the digits above the division symbol: 13. Therefore, 91 ÷ 7 = 13.
2. Repeated Subtraction
This method involves repeatedly subtracting the divisor from the dividend until you reach zero or a number smaller than the divisor. The number of times you subtract is the quotient.
91 - 7 = 84 84 - 7 = 77 77 - 7 = 70 70 - 7 = 63 63 - 7 = 56 56 - 7 = 49 49 - 7 = 42 42 - 7 = 35 35 - 7 = 28 28 - 7 = 21 21 - 7 = 14 14 - 7 = 7 7 - 7 = 0
We subtracted 7 thirteen times, confirming that 91 ÷ 7 = 13. While effective for smaller numbers, this method becomes cumbersome with larger dividends.
3. Multiplication Tables
If you know your multiplication tables well, you can quickly identify that 7 multiplied by 13 equals 91 (7 x 13 = 91). This directly gives you the answer to the division problem. This is the most efficient method for those familiar with multiplication facts.
The Mathematical Principles Behind Division
The division problem 91 ÷ 7 demonstrates several core mathematical principles:
-
Inverse Operation: Division is the inverse operation of multiplication. Just as multiplication involves repeated addition, division involves repeated subtraction.
-
Factors and Multiples: The numbers 7 and 13 are factors of 91, meaning they divide 91 without leaving a remainder. Conversely, 91 is a multiple of both 7 and 13.
-
Remainders: Division problems don't always result in whole numbers. If the dividend isn't perfectly divisible by the divisor, there's a remainder. For example, 92 ÷ 7 would result in a quotient of 13 with a remainder of 1.
-
Distributive Property: This property states that a number can be divided by a sum or difference of numbers. For instance, we could break down 91 into (70 + 21) and divide each part by 7 separately: (70 ÷ 7) + (21 ÷ 7) = 10 + 3 = 13.
Real-World Applications of Division
Division is not just an abstract mathematical concept; it's a crucial tool used extensively in daily life and various professions. Some examples include:
- Sharing equally: Dividing a group of items (e.g., candies, toys) among friends.
- Calculating unit rates: Determining the price per item, speed per hour, or any other rate.
- Averaging: Finding the mean of a set of numbers.
- Scaling recipes: Adjusting ingredient quantities for different serving sizes.
- Financial calculations: Dividing total costs among multiple people or determining percentages.
- Engineering and construction: Calculating material requirements and dimensions.
Frequently Asked Questions (FAQ)
Q: What if I get a remainder when dividing 91 by 7?
A: You shouldn't get a remainder. 91 is perfectly divisible by 7. A remainder would indicate an error in the calculation.
Q: Are there other ways to represent the answer 13?
A: Yes, 13 can be represented in various forms, such as a Roman numeral (XIII), a binary number (1101), or as a fraction (<sup>26</sup>⁄<sub>2</sub>).
Q: How can I improve my division skills?
A: Practice is key! Work through various division problems of increasing difficulty. Master your multiplication tables, and use different methods to solve problems. Online resources and educational games can be helpful.
Q: Why is understanding division important?
A: Division is a fundamental building block of mathematics. A strong understanding of division is essential for mastering more advanced mathematical concepts such as fractions, decimals, percentages, algebra, and calculus. It's a critical skill for problem-solving in many areas of life.
Conclusion
The seemingly simple division problem 91 ÷ 7 provides a rich opportunity to explore the core concepts of division, its various solution methods, and its extensive real-world applications. By understanding the underlying principles and practicing different techniques, you can develop a strong foundation in arithmetic and enhance your problem-solving abilities. This deep dive into 91 divided by 7 showcases how even the most basic mathematical operations can be surprisingly intricate and rewarding to explore, laying a solid groundwork for further mathematical endeavors. Remember, the key is consistent practice and a genuine curiosity for the fascinating world of numbers.
Latest Posts
Latest Posts
-
11 Oz To Ml
Sep 25, 2025
-
Dissociation Of Sulphuric Acid
Sep 25, 2025
-
3 8 Kilometers In Miles
Sep 25, 2025
-
Boxers Motto Animal Farm
Sep 25, 2025
-
69 Celsius To Fahrenheit
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 91 Divided By 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.