Convert 1/5 Into Percentage
renascent
Sep 22, 2025 · 6 min read
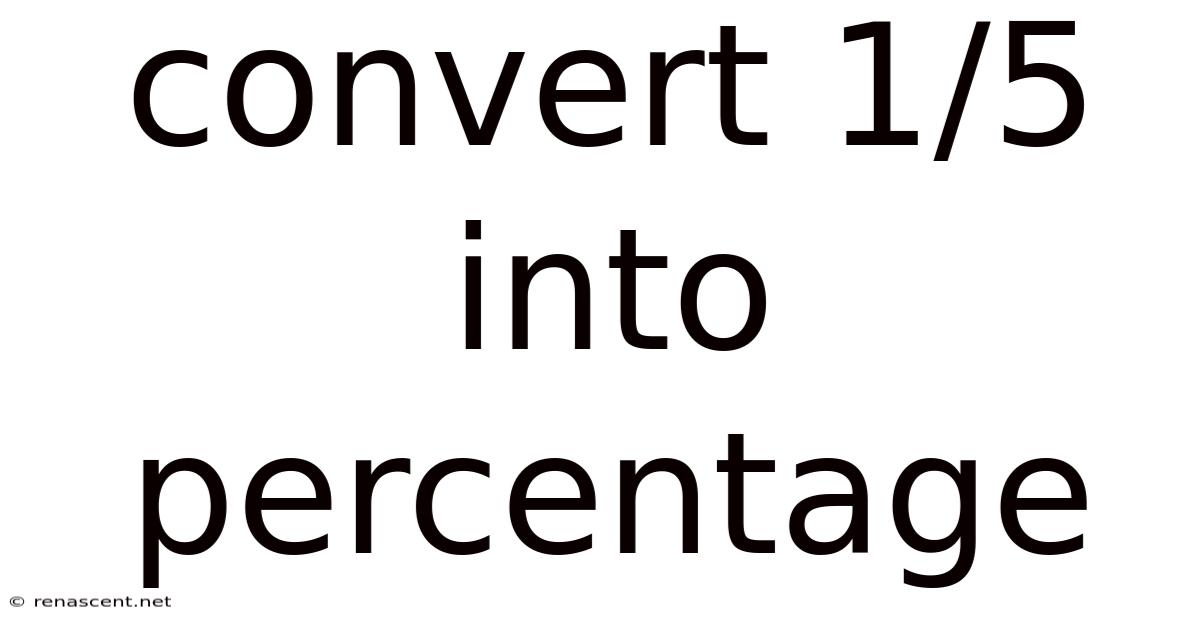
Table of Contents
Converting Fractions to Percentages: A Comprehensive Guide to Understanding 1/5 as a Percentage
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in shops to understanding statistical data. This article provides a comprehensive guide on how to convert fractions to percentages, using the example of 1/5, and delves into the underlying mathematical principles. We’ll explore various methods, address common misconceptions, and answer frequently asked questions, ensuring a thorough understanding of this essential concept.
Understanding Fractions and Percentages
Before diving into the conversion process, let's establish a clear understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/5, 1 is the numerator and 5 is the denominator. This means we have one part out of a total of five equal parts.
A percentage, on the other hand, is a way of expressing a fraction as a proportion of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Percentages are denoted by the symbol '%'. So, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the simplified fraction 1/2.
Method 1: Converting 1/5 to a Percentage using the Direct Method
The most straightforward method to convert a fraction to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator by the denominator. In our case, 1/5 = 1 ÷ 5 = 0.2
-
Multiply the decimal by 100: This converts the decimal to a percentage. 0.2 x 100 = 20%
Therefore, 1/5 is equal to 20%.
This method is applicable to any fraction. Simply divide the numerator by the denominator and then multiply the result by 100 to obtain the percentage equivalent.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
An alternative approach involves finding an equivalent fraction where the denominator is 100. This method is particularly useful for fractions that can be easily scaled up to a denominator of 100.
To convert 1/5 to a percentage using this method, we ask ourselves: "What number, when multiplied by 5, gives 100?" The answer is 20 (5 x 20 = 100).
To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by the same number. So, we multiply both the numerator and denominator of 1/5 by 20:
(1 x 20) / (5 x 20) = 20/100
Since a percentage represents parts per hundred, 20/100 is directly equivalent to 20%.
This method provides a visual representation of the fraction as a part of 100, reinforcing the concept of percentages. However, it's not always practical for fractions with denominators that don't easily scale to 100.
Method 3: Using Proportions to Convert 1/5 to a Percentage
This method uses the concept of proportions to solve for the percentage. We set up a proportion where one ratio represents the fraction and the other represents the percentage.
Let 'x' represent the percentage equivalent of 1/5. We can set up the following proportion:
1/5 = x/100
To solve for 'x', we cross-multiply:
5x = 100
Divide both sides by 5:
x = 20
Therefore, 1/5 is equal to 20%.
This method is mathematically rigorous and showcases the relationship between fractions and percentages in a clear and concise manner. It's a versatile method applicable to any fraction conversion.
Visualizing 1/5 as 20%
It's helpful to visualize the concept. Imagine a circle divided into five equal parts. If you shade one of these parts, you've shaded 1/5 of the circle. Now, imagine a larger circle divided into 100 equal parts. Shading 20 of these smaller parts would represent the same area as shading one part in the first circle. This visual representation clearly illustrates the equivalence of 1/5 and 20%.
Real-World Applications of Converting Fractions to Percentages
The ability to convert fractions to percentages is crucial in numerous real-world scenarios:
- Financial calculations: Calculating interest rates, discounts, tax rates, and profit margins. For example, a 20% discount on a $100 item means a reduction of $20.
- Statistical analysis: Interpreting data presented in fractions, such as survey results or test scores.
- Scientific measurements: Expressing experimental results or measurements as percentages.
- Everyday life: Understanding proportions in recipes, calculating tips, or determining sale prices.
Common Mistakes to Avoid When Converting Fractions to Percentages
Several common errors can occur when converting fractions to percentages:
- Incorrectly multiplying or dividing: Double-check your calculations to ensure accuracy. A simple mistake in multiplication or division can lead to an incorrect percentage.
- Forgetting to multiply by 100: This is a crucial step. Dividing the numerator by the denominator only gives you the decimal equivalent; multiplying by 100 converts it to a percentage.
- Incorrectly rounding: Rounding off decimals prematurely can result in an inaccurate percentage. It's best to maintain the full decimal value until the final calculation.
Frequently Asked Questions (FAQs)
Q1: Can all fractions be converted to percentages?
A1: Yes, all fractions can be converted to percentages. This is because percentages are simply another way of expressing fractions—a fraction with a denominator of 100.
Q2: What if the fraction results in a repeating decimal?
A2: If the division of the numerator by the denominator results in a repeating decimal, you can either express the percentage using the repeating decimal or round to a reasonable number of decimal places, depending on the context. For instance, 1/3 = 0.333..., which can be expressed as approximately 33.33%.
Q3: How do I convert percentages back to fractions?
A3: To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 20% = 20/100 = 1/5.
Q4: Are there any online calculators or tools that can help me convert fractions to percentages?
A4: Yes, many online calculators are available that can perform this conversion quickly and easily. However, understanding the underlying principles is crucial for applying this skill effectively.
Conclusion: Mastering Fraction to Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with vast applications across various fields. Understanding the different methods outlined in this article—the direct method, the equivalent fraction method, and the proportion method—will equip you with the necessary tools to confidently perform this conversion. Remember to practice regularly and avoid common mistakes to solidify your understanding and build proficiency in this essential skill. The ability to fluently translate between fractions and percentages enhances your numerical literacy and problem-solving capabilities, empowering you to tackle mathematical challenges with increased confidence and understanding. By mastering this concept, you unlock a crucial tool for navigating the numerical world around us.
Latest Posts
Latest Posts
-
165 Fahrenheit In Celsius
Sep 22, 2025
-
Intermolecular Vs Intramolecular Forces
Sep 22, 2025
-
15 Percent Of 300
Sep 22, 2025
-
60 Litres To Gallons
Sep 22, 2025
-
Octopus Halal In Islam
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Convert 1/5 Into Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.