Integrate Sin 2 X
renascent
Sep 24, 2025 · 6 min read
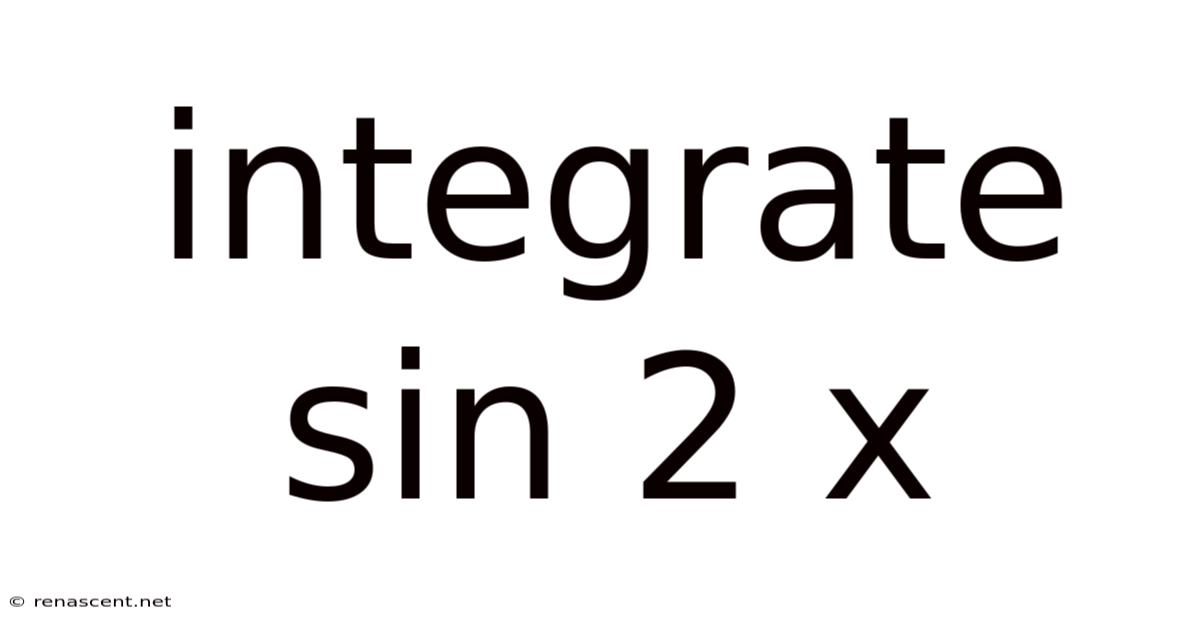
Table of Contents
Integrating sin²x: A Comprehensive Guide
Integrating trigonometric functions is a crucial skill in calculus, often encountered in physics, engineering, and other scientific fields. This article provides a thorough exploration of integrating sin²x, covering various methods, explanations, and common applications. We'll delve into the underlying principles, showcasing multiple approaches to solve this integral, making it accessible to students of all levels, from beginners grappling with basic integration techniques to those seeking a deeper understanding of advanced trigonometric identities. Understanding this integral unlocks the ability to tackle more complex integrals involving trigonometric functions.
Introduction: Understanding the Challenge
The integral of sin²x, denoted as ∫sin²x dx, isn't immediately solvable using basic integration rules. Unlike ∫sinx dx which directly integrates to -cosx + C, sin²x requires a clever approach. This is because we can't directly apply the power rule of integration to trigonometric functions squared. We need to employ trigonometric identities to transform the integrand into a more manageable form. This article will illustrate several effective strategies to accomplish this.
Method 1: Using the Power-Reducing Formula
The most common and arguably the most elegant method involves using the power-reducing formula (also known as the half-angle formula):
sin²x = (1 - cos2x)/2
This identity transforms the squared sine function into a linear combination of 1 and cos2x, both of which are easily integrable. Let's apply this to our integral:
∫sin²x dx = ∫(1 - cos2x)/2 dx
Now, we can integrate term by term:
= (1/2) ∫1 dx - (1/2) ∫cos2x dx
The integral of 1 with respect to x is simply x, and the integral of cos2x is (1/2)sin2x. Therefore:
= (1/2)x - (1/4)sin2x + C
Where 'C' represents the constant of integration. This is the general solution to the integral of sin²x.
Method 2: Using Integration by Parts
While less straightforward for this specific integral, integration by parts offers an alternative approach. The integration by parts formula is:
∫u dv = uv - ∫v du
Let's choose:
u = sinx => du = cosx dx dv = sinx dx => v = -cosx
Applying the integration by parts formula:
∫sin²x dx = sinx(-cosx) - ∫(-cosx)(cosx) dx
= -sinxcosx + ∫cos²x dx
Now, we use the Pythagorean identity: cos²x = 1 - sin²x
= -sinxcosx + ∫(1 - sin²x) dx
= -sinxcosx + ∫1 dx - ∫sin²x dx
Notice that the original integral, ∫sin²x dx, appears on both sides of the equation. We can solve for it algebraically:
2∫sin²x dx = -sinxcosx + x + C
∫sin²x dx = (-sinxcosx + x)/2 + C
This approach might seem more complex than the power-reducing formula, but it demonstrates the versatility of integration by parts and its applicability even when a simpler method exists. It also highlights the importance of algebraic manipulation in solving complex integrals.
Method 3: Using Complex Exponentials (Euler's Formula)
For those comfortable with complex numbers, Euler's formula provides another fascinating approach. Euler's formula states:
e^(ix) = cosx + i sinx
From this, we can derive:
sinx = (e^(ix) - e^(-ix))/(2i)
Therefore, sin²x becomes:
sin²x = [(e^(ix) - e^(-ix))/(2i)]² = -(e^(2ix) - 2 + e^(-2ix))/4
Integrating this expression:
∫sin²x dx = -(1/4)∫(e^(2ix) - 2 + e^(-2ix)) dx
= -(1/4)[(1/(2i))e^(2ix) - 2x + (-1/(2i))e^(-2ix)] + C
Simplifying using Euler's formula again and some algebraic manipulation leads back to the same result:
= x/2 - (sin2x)/4 + C
Detailed Explanation of the Power-Reducing Formula
The power-reducing formula, sin²x = (1 - cos2x)/2, is derived from the double-angle formula for cosine:
cos2x = cos²(x) - sin²(x)
We also know that cos²(x) = 1 - sin²(x). Substituting this into the double-angle formula:
cos2x = (1 - sin²(x)) - sin²(x) = 1 - 2sin²(x)
Solving for sin²(x):
2sin²(x) = 1 - cos2x
sin²(x) = (1 - cos2x)/2
This derivation highlights the interconnectedness of trigonometric identities and how one identity can be used to derive others. Understanding these relationships is essential for efficient problem-solving in calculus.
Common Applications and Examples
The integral of sin²x has numerous applications in various fields. A few examples include:
-
Calculating areas under curves: Finding the area enclosed by the curve y = sin²x and the x-axis over a specific interval.
-
Solving differential equations: Differential equations involving sinusoidal functions frequently require integrating sin²x as part of the solution process.
-
Physics and Engineering: Many physical phenomena, such as wave motion and oscillations, involve sinusoidal functions. Integrating sin²x is crucial for analyzing these phenomena. For instance, calculating the average power of an alternating current (AC) signal often necessitates this integral.
-
Probability and Statistics: The integral appears in certain probability density functions, particularly those related to periodic or cyclical processes.
Example: Find the area under the curve y = sin²x from x = 0 to x = π.
Solution: We need to evaluate the definite integral:
∫(from 0 to π) sin²x dx =
= [(π/2) - (sin2π)/4] - [(0/2) - (sin0)/4] = π/2
Therefore, the area under the curve is π/2 square units.
Frequently Asked Questions (FAQ)
Q1: What is the difference between ∫sin²x dx and ∫sin x² dx?
A1: These are very different integrals. ∫sin²x dx refers to the square of the sine function, while ∫sin x² dx is the sine of x². The first can be solved using the methods described above. The second integral, however, does not have a closed-form solution in terms of elementary functions. It requires numerical methods for approximation.
Q2: Can I use a calculator or software to solve this integral?
A2: While many calculators and mathematical software packages (like Mathematica or Maple) can directly compute definite integrals, understanding the underlying methods is crucial for tackling more complex problems and gaining a deeper conceptual understanding. These tools can be used to verify results but not as a replacement for understanding the integration process.
Q3: What happens if the integral is more complex, such as ∫sin²(2x) dx or ∫x sin²x dx?
A3: For ∫sin²(2x) dx, you would use a substitution (u = 2x) and then apply the power-reducing formula as before. For ∫x sin²x dx, you'd likely use integration by parts, choosing u = x and dv = sin²x dx (remembering you'll need to integrate sin²x first using the methods described above).
Conclusion
Integrating sin²x is a fundamental exercise in calculus that underscores the power of trigonometric identities and various integration techniques. This article has explored three different methods—using the power-reducing formula, integration by parts, and complex exponentials—to solve this integral, providing a comprehensive understanding of the underlying principles. Mastering this integral lays a strong foundation for tackling more intricate integration problems involving trigonometric functions and paves the way for understanding their applications in diverse scientific and engineering fields. Remember to always consider the context of the problem and choose the most efficient method for solving the integral. Practice is key to mastering these techniques.
Latest Posts
Latest Posts
-
7 12 To A Decimal
Sep 24, 2025
-
14000 Grams To Kg
Sep 24, 2025
-
R404a Pressure Temp Chart
Sep 24, 2025
-
Contingency In A Sentence
Sep 24, 2025
-
Sara Ann Haney Brings Plenty
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Integrate Sin 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.