Lcm 3 And 9
renascent
Sep 24, 2025 · 7 min read
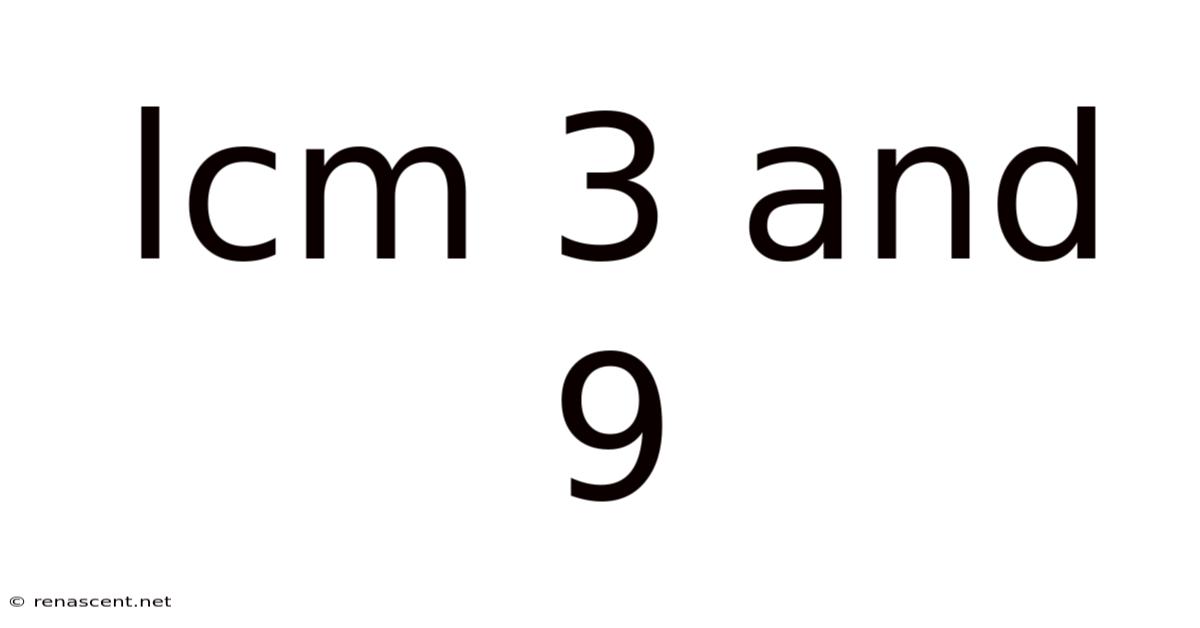
Table of Contents
Unveiling the Secrets of LCM: A Deep Dive into Finding the Least Common Multiple of 3 and 9
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 3 and 9. However, understanding the underlying principles behind LCM calculations is crucial for mastering more complex mathematical concepts later on. This comprehensive guide will not only show you how to find the LCM of 3 and 9 but will also explore the broader concept of LCM, its applications, and different methods of calculation. We'll delve into the theory, provide step-by-step examples, and even address some frequently asked questions. By the end, you'll have a solid grasp of LCM and its significance in mathematics.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the numbers you're working with as factors. For example, if we're looking for the LCM of 2 and 3, we're searching for the smallest number that's divisible by both 2 and 3. That number is 6.
Why is understanding LCM important? It's a fundamental concept used extensively in various mathematical applications, including:
- Fraction Arithmetic: Finding the LCM of denominators is essential when adding or subtracting fractions.
- Solving Equations: LCM is sometimes used to simplify equations involving fractions or rational expressions.
- Scheduling Problems: LCM helps in determining the timing of recurring events, like bus schedules or the meeting times of different groups.
- Modular Arithmetic: LCM plays a key role in understanding modular arithmetic, which has applications in cryptography and computer science.
Methods for Calculating LCM
There are several ways to calculate the LCM, each with its own advantages and disadvantages. Let's explore the most common methods, focusing on how they apply to finding the LCM of 3 and 9.
1. Listing Multiples Method
This method is straightforward and easy to understand, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple that appears in both lists.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21...
- Multiples of 9: 9, 18, 27, 36...
Notice that 9 is the smallest number that appears in both lists. Therefore, the LCM of 3 and 9 is 9.
This method works well for small numbers but becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors.
- Prime Factorization of 3: 3 (3 is a prime number)
- Prime Factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization:
- Identify the prime factors: The prime factors are 3.
- Find the highest power of each prime factor: The highest power of 3 is 3².
- Multiply the highest powers: 3² = 9
Therefore, the LCM of 3 and 9 is 9. This method is particularly useful when dealing with larger numbers where listing multiples would be cumbersome.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. The formula is:
LCM(a, b) * GCD(a, b) = a * b
First, let's find the GCD of 3 and 9. The GCD is the largest number that divides both 3 and 9 without leaving a remainder. In this case, the GCD(3, 9) = 3.
Now, we can use the formula:
LCM(3, 9) * GCD(3, 9) = 3 * 9 LCM(3, 9) * 3 = 27 LCM(3, 9) = 27 / 3 LCM(3, 9) = 9
Why is the LCM of 3 and 9 equal to 9? A Deeper Look
The LCM of 3 and 9 being 9 makes intuitive sense when you consider the relationship between these two numbers. 9 is a multiple of 3 (3 x 3 = 9). Therefore, any number that is a multiple of 9 is automatically a multiple of 3. This means that the smallest number divisible by both 3 and 9 is simply 9 itself. This illustrates a key property of LCM: if one number is a multiple of the other, the LCM is the larger number.
LCM in Real-World Applications: Beyond the Classroom
The concept of LCM extends far beyond textbook examples. It's a practical tool with numerous applications in everyday life and various fields:
-
Scheduling and Planning: Imagine you have two machines that perform different tasks in a manufacturing process. One machine completes its cycle every 3 minutes, and the other every 9 minutes. Using LCM, we can determine that both machines will complete their cycles simultaneously every 9 minutes, optimizing production scheduling.
-
Music and Rhythm: In music, the LCM helps determine the least common denominator of rhythmic patterns. This ensures that different instruments playing together create a harmonizing rhythm. If one instrument has a rhythm repeating every 3 beats, and another repeats every 9 beats, they'll synchronize every 9 beats.
-
Construction and Engineering: In construction, LCM helps in determining the optimal lengths for materials or in aligning different structural elements.
-
Computer Science: LCM is important in algorithm design, especially when dealing with processes that repeat at different intervals. For instance, synchronizing tasks in operating systems might utilize LCM principles.
These are just a few examples. The ability to calculate and understand LCM is a versatile skill that can be applied across diverse fields.
Frequently Asked Questions (FAQ)
Q: What if I want to find the LCM of more than two numbers?
A: The methods described above can be extended to find the LCM of multiple numbers. For the prime factorization method, you would find the prime factorization of each number, identify the highest power of each prime factor present, and then multiply those highest powers together. For the listing method, you'd list multiples of each number until you find the smallest common multiple among all the lists.
Q: Is there a shortcut for finding the LCM of two numbers if one is a multiple of the other?
A: Yes! If one number is a multiple of the other, the LCM is simply the larger number.
Q: How does the LCM relate to the GCD?
A: The LCM and GCD are inversely related. As the GCD increases, the LCM decreases, and vice-versa. Their product is always equal to the product of the two original numbers.
Q: Are there any online calculators or tools to help me find the LCM?
A: Yes, numerous online calculators are available that can quickly compute the LCM of any set of numbers. These can be helpful for checking your work or for dealing with larger numbers.
Q: Why is understanding LCM important for fractions?
A: When adding or subtracting fractions, you need to find a common denominator. The LCM of the denominators provides the least common denominator, simplifying the calculation and resulting in a fraction in its simplest form.
Conclusion: Mastering the Art of LCM
Finding the LCM of 3 and 9, while seemingly simple, serves as a gateway to understanding a fundamental concept in mathematics. By mastering different methods of LCM calculation, you're not just solving arithmetic problems; you're building a solid foundation for more advanced mathematical concepts and practical applications across various fields. Whether you’re a student tackling fractions, a musician harmonizing rhythms, or an engineer planning a project, the ability to efficiently calculate the least common multiple will prove to be an invaluable skill. Remember to practice using different methods to solidify your understanding and choose the most efficient approach based on the numbers involved. The journey of understanding LCM is a testament to the power of fundamental mathematical concepts in shaping our understanding of the world around us.
Latest Posts
Latest Posts
-
Dynamic Vs Static Equilibrium
Sep 24, 2025
-
75 Percent Of 60
Sep 24, 2025
-
102 Celsius To Fahrenheit
Sep 24, 2025
-
157 Pounds In Kilograms
Sep 24, 2025
-
Certificates Of Deposit Australia
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm 3 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.