Square Root Of 28
renascent
Sep 24, 2025 · 5 min read
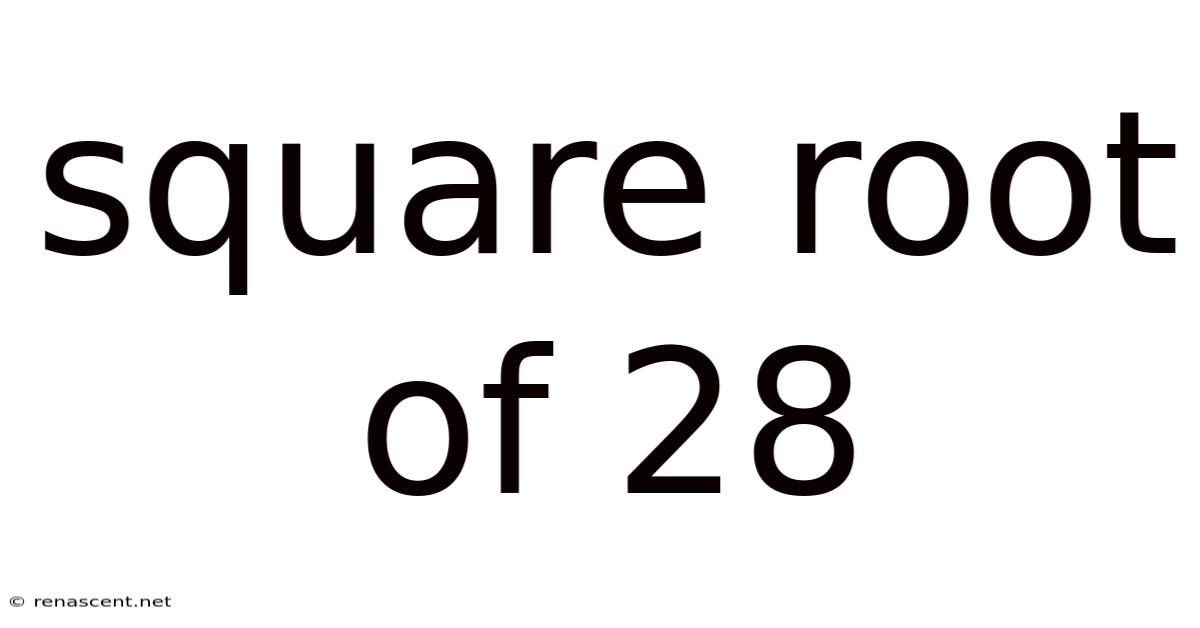
Table of Contents
Unveiling the Mysteries of the Square Root of 28: A Deep Dive into Irrational Numbers
Finding the square root of 28 might seem like a simple mathematical task, but it opens a fascinating window into the world of irrational numbers and the beauty of mathematical approximation. This article will explore the square root of 28 in depth, examining different methods for calculating it, its properties, and its significance within the broader context of mathematics. We'll delve into both practical calculations and the theoretical underpinnings, making this a comprehensive guide suitable for students and enthusiasts alike.
Understanding Square Roots
Before we tackle the specifics of the square root of 28, let's refresh our understanding of square roots. The square root of a number (x) is a value (y) that, when multiplied by itself, equals x. In simpler terms, y * y = x. For example, the square root of 9 is 3 because 3 * 3 = 9. This is denoted as √9 = 3.
However, not all numbers have perfect square roots – integers that result in a whole number when squared. Many numbers, like 28, have irrational square roots. Irrational numbers cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representation continues infinitely without repeating. This is where the complexities – and the intrigue – begin.
Calculating the Square Root of 28: Methods and Approximations
There are several ways to approximate the square root of 28. Let's examine a few:
1. Prime Factorization and Simplification:
The first step is to find the prime factorization of 28. 28 can be broken down into 2 x 2 x 7. Therefore, √28 = √(2 x 2 x 7) = √(2² x 7) = 2√7. This simplifies the calculation, as we only need to find the square root of 7, a smaller number. However, √7 is still irrational.
2. Babylonian Method (or Heron's Method):
This iterative method provides a successively closer approximation of the square root. It's based on repeatedly refining an initial guess.
- Step 1: Make an initial guess. Let's guess 5 (since 5 x 5 = 25, which is close to 28).
- Step 2: Improve the guess. Divide the number (28) by the guess (5) and then average the result with the original guess: (5 + 28/5) / 2 = 5.3.
- Step 3: Repeat Step 2. Use the new guess (5.3) to repeat the process: (5.3 + 28/5.3) / 2 ≈ 5.2915.
- Step 4: Continue iterating. Each iteration brings the approximation closer to the actual value. The more iterations you perform, the more precise the result becomes.
3. Using a Calculator:
The easiest way to find a decimal approximation is using a calculator. Most calculators have a square root function (√). Inputting 28 will give you a decimal approximation, usually around 5.2915026221... This decimal representation goes on infinitely, highlighting the irrational nature of √28.
Understanding the Irrationality of √28
The fact that √28 is irrational has significant mathematical implications. It cannot be expressed as a fraction, meaning its decimal representation is non-terminating and non-repeating. This is a fundamental characteristic of irrational numbers, which comprise a vast majority of the real numbers. The proof of the irrationality of √2 is often used as a model for proving the irrationality of other square roots, such as √28, given that it simplifies to 2√7, and √7 is also irrational. These proofs often employ techniques like proof by contradiction.
Applications of Square Roots and √28
Square roots have numerous applications across various fields:
- Geometry: Calculating distances, areas, and volumes frequently involves square roots (e.g., finding the diagonal of a square, the hypotenuse of a right-angled triangle using the Pythagorean theorem). If you have a square with an area of 28 square units, the length of its side would be √28 units.
- Physics: Many physics equations incorporate square roots. For instance, calculations involving velocity, energy, and acceleration might require finding square roots.
- Engineering: Engineering designs and calculations, particularly in structural engineering, often use square roots to solve problems related to stress, strain, and stability.
- Computer Graphics: Square roots are integral to algorithms used in computer graphics and image processing. They are crucial for calculations involving distances and transformations.
Approximating √28 using Continued Fractions
Another interesting method for approximating irrational numbers is using continued fractions. A continued fraction is an expression of the form:
a₀ + 1/(a₁ + 1/(a₂ + 1/(a₃ + ...)))
where a₀, a₁, a₂, a₃,... are integers. Every irrational number can be represented by a unique infinite continued fraction. While calculating the full continued fraction for √28 is beyond the scope of this introductory explanation, the initial terms can be computed. These initial terms give successively better rational approximations of √28.
Frequently Asked Questions (FAQ)
Q: Is √28 a rational or irrational number?
A: √28 is an irrational number because it cannot be expressed as a fraction of two integers. Its decimal representation is infinite and non-repeating.
Q: How can I calculate √28 without a calculator?
A: You can use methods like the Babylonian method or approximations based on the prime factorization (2√7). However, these methods will only yield approximations, not the exact value.
Q: What is the significance of irrational numbers like √28?
A: Irrational numbers demonstrate the richness and complexity of the number system. They are essential for many mathematical and scientific calculations and show that not all numbers can be neatly expressed as fractions.
Q: Are there other ways to approximate √28?
A: Yes, there are numerous numerical methods for approximating square roots, including Newton-Raphson method and Taylor series expansions. These methods are more advanced and usually involve calculus.
Conclusion
The seemingly simple task of finding the square root of 28 reveals a deeper understanding of irrational numbers, approximation techniques, and the fascinating interplay between pure mathematics and its practical applications. Whether using a calculator, applying the Babylonian method, or exploring the world of continued fractions, understanding how to approximate and work with irrational numbers like √28 is crucial for anyone pursuing a path in mathematics, science, or engineering. The journey to understand √28 is not just about finding a numerical answer; it's about appreciating the elegance and complexity inherent in the mathematical world around us. The more we delve into these seemingly simple concepts, the more we discover the profound beauty and utility of mathematics.
Latest Posts
Latest Posts
-
How Ussteele Wall Streetjournal
Sep 24, 2025
-
Mass Density Of Brass
Sep 24, 2025
-
How To Uninstall Zscaler
Sep 24, 2025
-
All Factors For 40
Sep 24, 2025
-
0 4 In Fraction Form
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.