What Is 90 2
renascent
Sep 16, 2025 · 5 min read
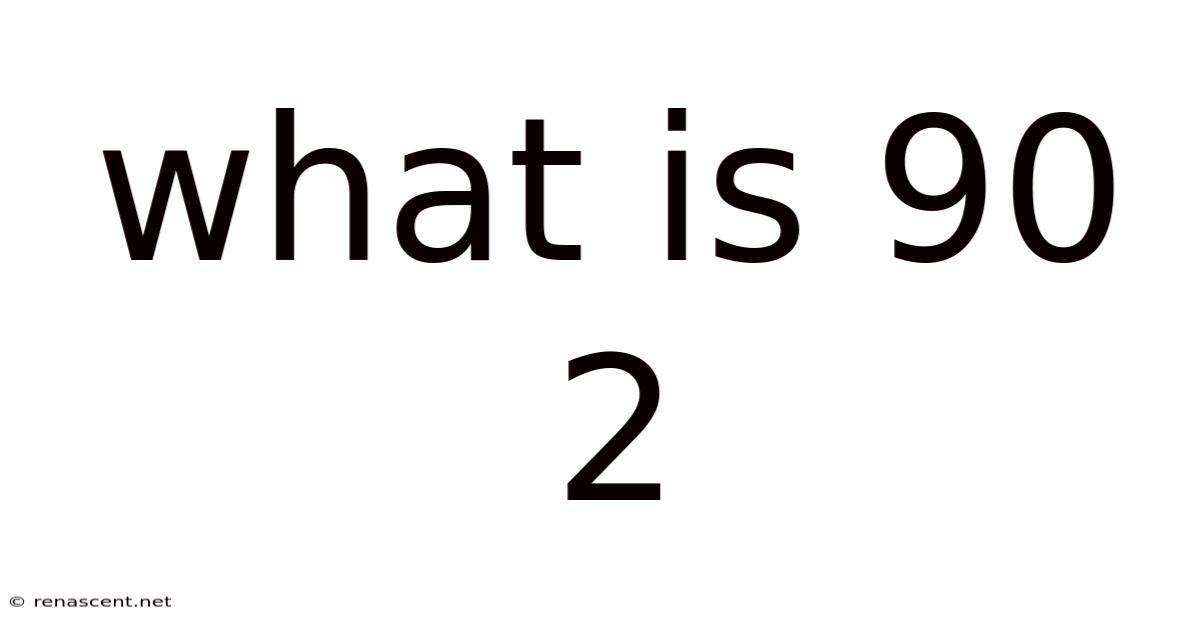
Table of Contents
Decoding 90²: Exploring Squares, Exponents, and Their Applications
What is 90²? This seemingly simple question opens the door to a deeper understanding of fundamental mathematical concepts, specifically squares and exponents. This article will not only answer the question directly but delve into the broader context of exponentiation, exploring its applications in various fields and addressing common misconceptions. We'll break down the concept in a way that's accessible to everyone, from beginners to those looking for a refresher.
Understanding Squares and Exponents
Before tackling 90², let's establish a solid foundation. The expression 90² represents the square of 90. A square, in mathematics, is the result of multiplying a number by itself. More generally, this is an example of exponentiation, where a number (the base) is raised to a power (the exponent). In 90², 90 is the base and 2 is the exponent.
The exponent indicates how many times the base is multiplied by itself. So, 90² means 90 multiplied by itself twice: 90 x 90.
Therefore, 90² = 8100.
Calculating 90²: Methods and Approaches
While the answer is straightforward, let's explore different ways to calculate 90², highlighting the underlying mathematical principles:
-
Direct Multiplication: The most basic approach is simply multiplying 90 by 90. This can be done manually, using a calculator, or even through mental math techniques (e.g., breaking down 90 as 9 x 10 and then squaring).
-
Distributive Property: We can leverage the distributive property of multiplication. We can rewrite 90 as (9 x 10) and then apply the rule (ab)² = a²b². This gives us (9 x 10)² = 9² x 10² = 81 x 100 = 8100. This method showcases a more strategic approach to multiplication.
-
Using the Properties of Exponents: Understanding the properties of exponents is crucial for more complex calculations. One relevant property is (a x b)^n = a^n x b^n. Applying this to 90², we get: (9 x 10)² = 9² x 10² = 81 x 100 = 8100.
Beyond 90²: Exploring Exponents and Their Applications
The concept of exponents extends far beyond squaring a number. Let's explore the broader context:
-
Higher Powers: We can raise 90 to any power, not just 2. For example, 90³ (90 cubed) means 90 x 90 x 90 = 729000. The exponent dictates the number of times the base is multiplied by itself.
-
Fractional Exponents: Exponents can also be fractions. For example, 90^(1/2) represents the square root of 90, approximately 9.487. Fractional exponents introduce the concept of roots.
-
Negative Exponents: A negative exponent means the reciprocal of the base raised to the positive exponent. For instance, 90⁻¹ = 1/90. Negative exponents are crucial in various scientific and engineering applications.
-
Zero Exponent: Any number (except 0) raised to the power of 0 is equal to 1. This seemingly counterintuitive rule has significant implications in mathematical manipulations.
Exponents in Real-World Applications
The concept of exponents and squares isn't limited to abstract mathematical exercises. It has numerous real-world applications across various disciplines:
-
Geometry and Area Calculations: Calculating the area of a square directly uses the concept of squaring. If a square has a side length of 90 units, its area is 90² = 8100 square units. Similarly, calculating the volume of a cube involves cubing the side length.
-
Physics and Engineering: Exponents are ubiquitous in physics and engineering formulas. For example, the kinetic energy of an object is proportional to the square of its velocity (KE = 1/2mv²). Understanding exponents is crucial for interpreting and applying these formulas.
-
Finance and Compound Interest: Compound interest calculations rely heavily on exponents. The formula for compound interest involves raising the principal amount to a power that reflects the number of compounding periods.
-
Computer Science and Data Storage: Exponents play a significant role in data storage and processing. Binary numbers, the foundation of computer systems, utilize powers of 2. Understanding exponential growth is essential in analyzing algorithms and data structures.
-
Biology and Population Growth: Exponential growth models are often used to describe population growth (both human and other species). Understanding the principles of exponential growth is vital in ecology and population studies.
Common Misconceptions about Exponents
Several common misconceptions surround the use of exponents:
-
Misunderstanding the Order of Operations (PEMDAS/BODMAS): Remember the order of operations: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). Failing to follow this order can lead to incorrect calculations.
-
Incorrectly Applying Exponent Rules: Carefully review and understand the rules of exponents before applying them to calculations. Common errors involve incorrectly distributing exponents over addition or subtraction.
-
Confusing Squares with Doubling: Squaring a number is not the same as doubling it. Doubling a number means multiplying it by 2, while squaring means multiplying it by itself.
-
Misinterpreting Negative Exponents: Remember that a negative exponent does not indicate a negative result. Instead, it represents the reciprocal of the base raised to the positive exponent.
Frequently Asked Questions (FAQs)
Q: What is the difference between 90² and 2 x 90?
A: 90² (90 squared) means 90 x 90 = 8100, while 2 x 90 means 2 multiplied by 90, which equals 180. These are distinctly different operations.
Q: How can I calculate large exponents without a calculator?
A: For larger exponents, using logarithmic properties or approximation techniques might be necessary. Manual calculation becomes increasingly complex with higher exponents.
Q: Are there any online tools to calculate exponents?
A: Yes, numerous online calculators and mathematical software packages can efficiently calculate exponents of any size.
Q: What is the significance of exponents in higher-level mathematics?
A: Exponents form the foundation for various advanced mathematical concepts, including logarithms, exponential functions, and calculus. They play a crucial role in modelling and analyzing complex systems.
Conclusion
This exploration of 90² has provided a comprehensive look at the broader world of exponents. From basic multiplication to its real-world applications, understanding exponents is crucial for anyone seeking a deeper understanding of mathematics and its role in various fields. By mastering the principles discussed here, you can confidently tackle more complex mathematical problems and appreciate the power and elegance of this fundamental concept. Remember that consistent practice and a solid grasp of the underlying principles will pave your way to success in mathematics and beyond.
Latest Posts
Latest Posts
-
Mac Address From Ping
Sep 16, 2025
-
5250 Divided By 2
Sep 16, 2025
-
154 Lb To Kg
Sep 16, 2025
-
X 22 X 2
Sep 16, 2025
-
138 Pounds To Kilos
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 90 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.